Lecture 3
How to choose W?
loss function tells us how bad W is.
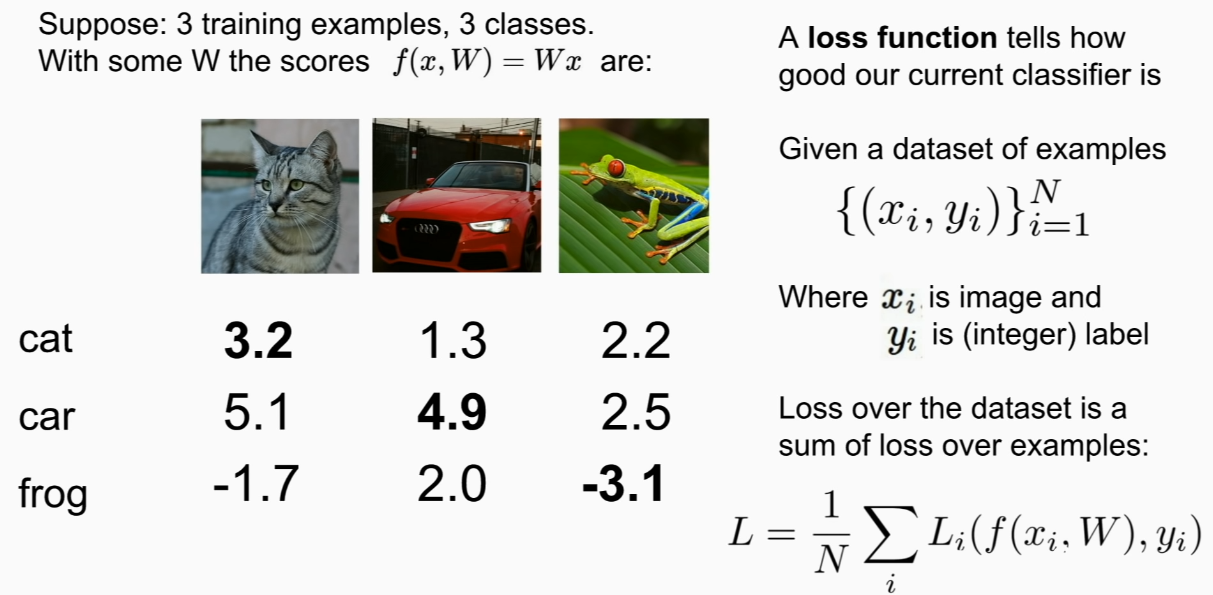
Multi class SVM loss == Hinge Loss

where
is ith image
is ith label
is score of j th class
is score of true class (correct class) for ith image
sum all the incorrect categories
compare collect category score
if score of collect category is higher than incorrect category by some safety margin (1 in this case)
sum and divide by total n
zero to inf value possible
we are happy if true score is much more higher than others
def L_i_vectorized(x, y, W):
"""
A faster half-vectorized implementation. half-vectorized
refers to the fact that for a single example the implementation contains
no for loops, but there is still one loop over the examples (outside this function)
"""
delta = 1.0
scores = W.dot(x)
# compute the margins for all classes in one vector operation
margins = np.maximum(0, scores - scores[y] + delta)
# on y-th position scores[y] - scores[y] canceled and gave delta. We want
# to ignore the y-th position and only consider margin on max wrong class
margins[y] = 0
loss_i = np.sum(margins)
return loss_i
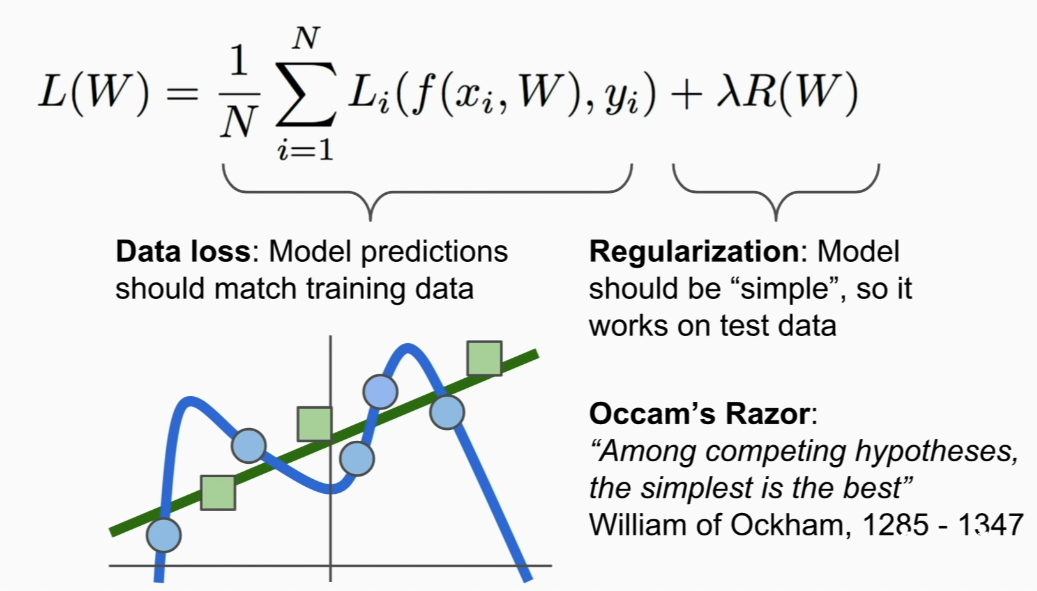
if we only consider train data (blue circle),
blue curve is made by the loss, but we want green line (more generalized)
to do that we add Regularization term R
hyperparam- lambda trades off data loss and regularization loss!
Occam's Razor
many different competing hypotheses=> generally prefer simpler one => cuz it more likley to generalize to new observations in the future
Regularization

l2 prefers spreaded not robust to outlier
l1 is more robust to outlier+
Softmax Classifier (Multinomial Logistic Regression)

using the scores, compute a probability distribution over classes

Q1. min max of L_i(softmax losS)? => min: log(1)=0 max: -log(0)=inf
to get probability of 1 and rest of them 0, scores must be inf and rest of them are -inf
therefore 0 value is theoritical min,max value
Q2. Uausally at initialization W is small so all s ≒0 what is the softmax loss?
-log(1/C)=log(C)
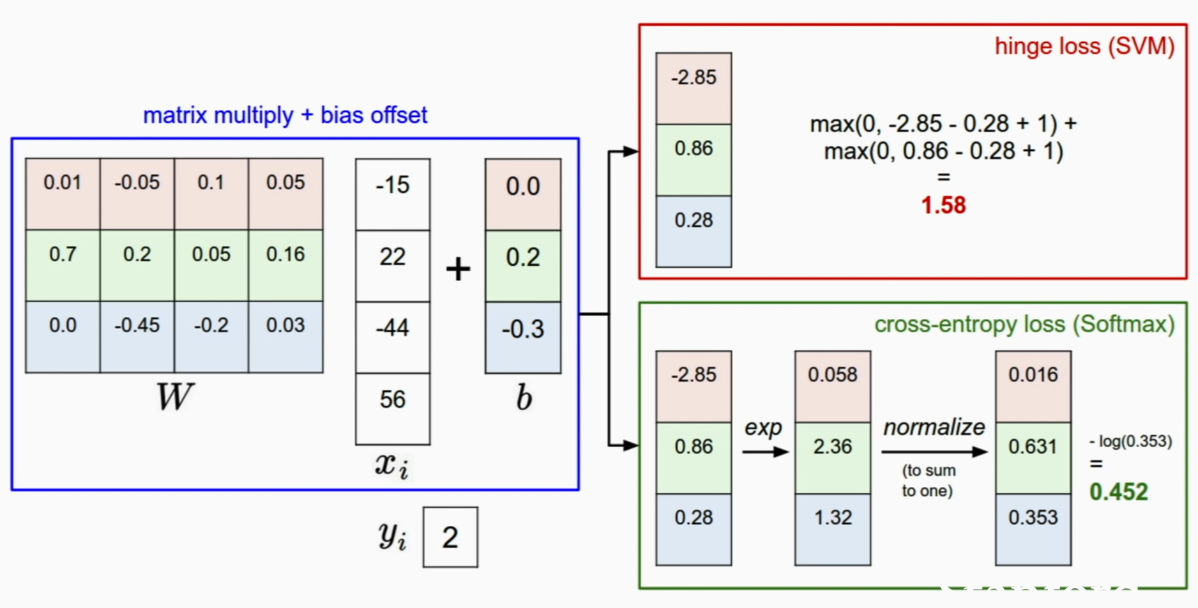
hinge loss sees the margins between scores of the correct class and the scores of the incorrect class
cross-entropy loss(softmax) compute probability distribution and see the -log Probabilty of correct class
svm loss does not care after certain point where margin is good enough to tell the differnce,but
softmax loss keeps to make the probability to 1
Optimization
how to find the path down to the valley?
use iterative solution
1. random search
take random W => cal loss => see which is the best
VERY BAD ALGORITHM
2. follow slope
slope => derivative of a func
gradient gives linear first order approximation to your function at your current point
so deep learning => cal gradient of function and use it to update parameter vector W
finite difference methods

calculate Numerical gradient: approximate slow, easy to write
Calculus!

analytic gradient: exact,fast,error-prone
use numerical gradient to check(gradient check)
Gradient Descent
init W with random values
# Vanilla Gradient Descent
while True:
weights_grad = evaluate_gradient(loss_fun, data, weights)
weights += - step_size * weights_grad # perform parameter updategradient points the greatest increase of the function
step_size(learning rate) => hparam.
how far do we step in the direction?
there are many diff update rules.
Stochastic Gradient Descent

if too much N, GD takes too much time.
# Vanilla Minibatch Gradient Descent
while True:
data_batch = sample_training_data(data, 256) # sample 256 examples
weights_grad = evaluate_gradient(loss_fun, data_batch, weights)
weights += - step_size * weights_grad # perform parameter updatenot calculating entire training set, but use approx sum of minibatch(small sample of training set)
like monte carlo rules.!
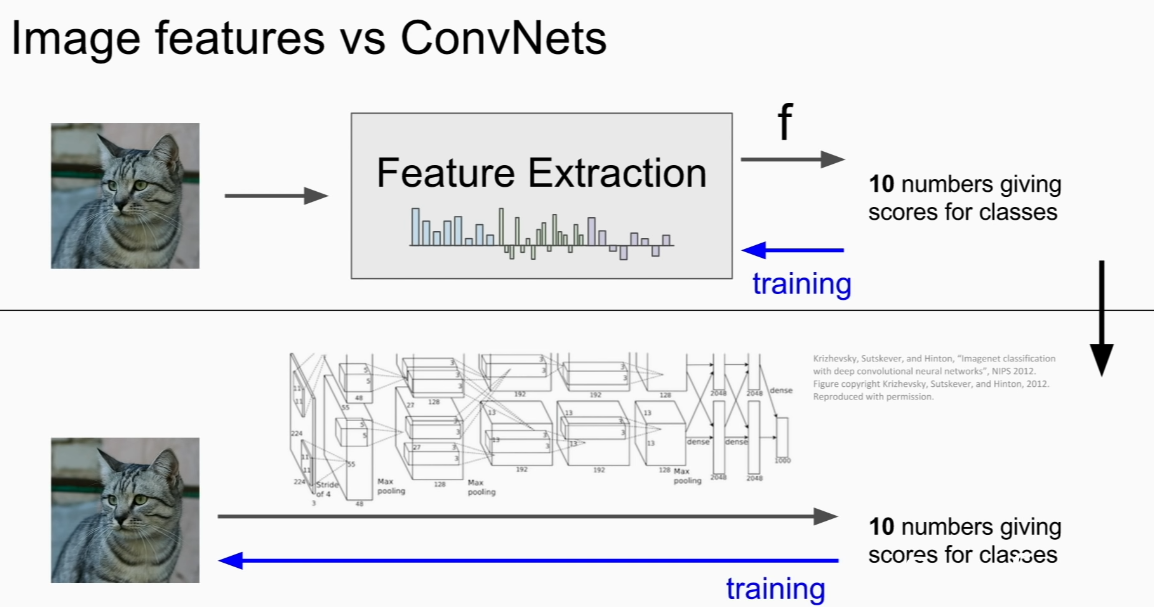
Image Features
image=>compute features=> concate => linear classifier
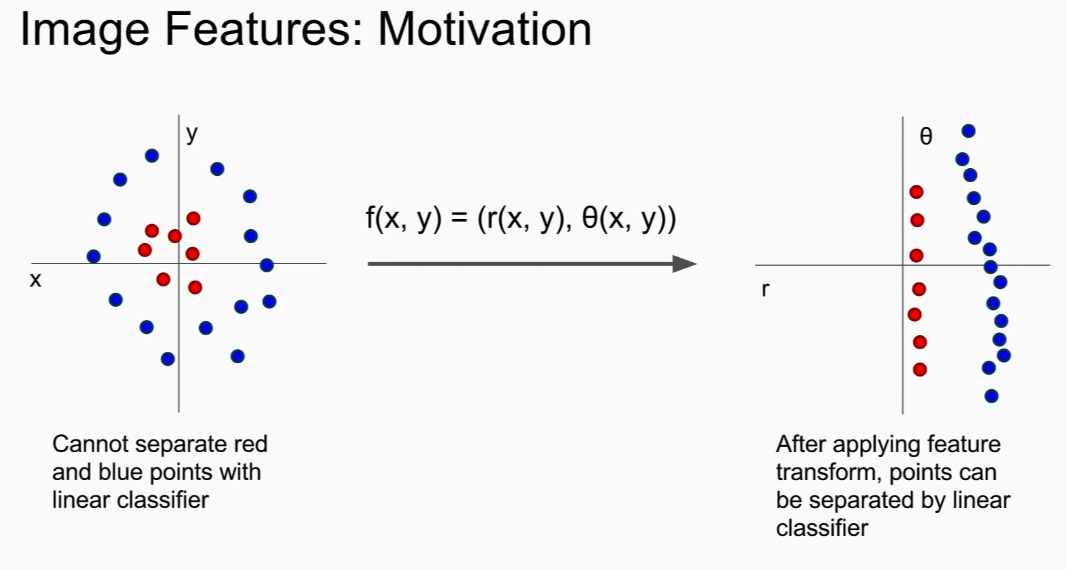
transform to polar coordinates, can linear seperate!
might work better than just using simple pixels!
Ex. Color Hstogram, Histogram of Oriented Gradienst(HoG)

divide pixels in to 8x8, find dominant edge direction and into histograms!
shows overall what edge infos in the image
Bag of Words
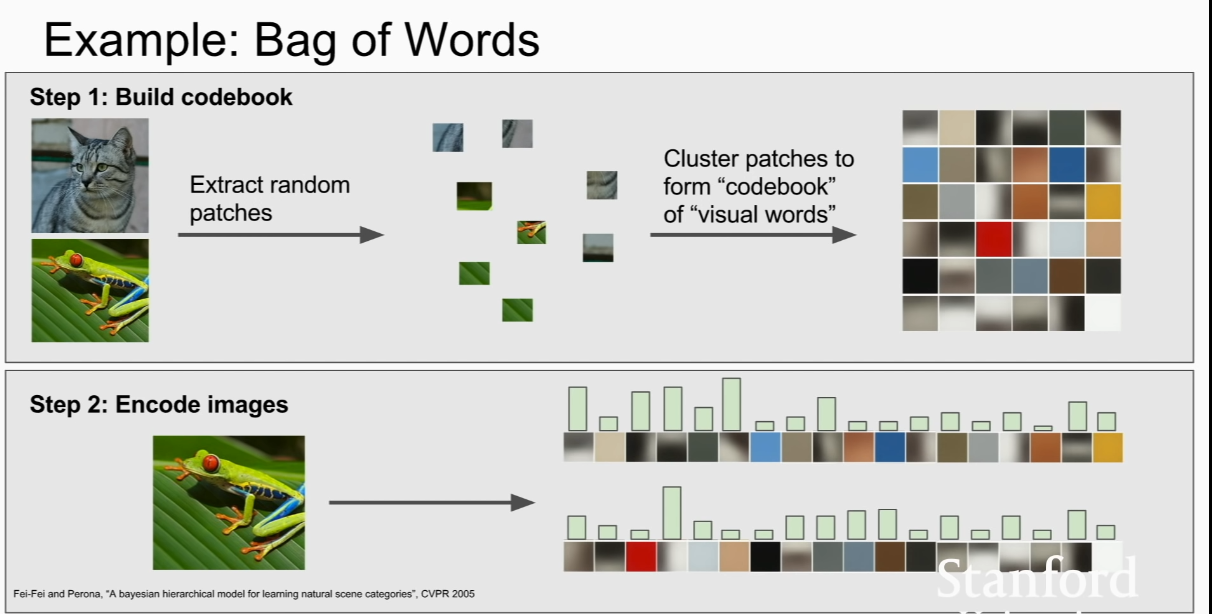
random crop images=> cluster them using K-means or smth ==> make codebook or visual words. => can get colors or oriented edges info!
see how many times does visual word occur in a image => info of image
Image Featuers VS CONV NETS