
문제
A company has n employees with a unique ID for each employee from 0 to n - 1.
The head of the company is the one with headID.
Each employee has one direct manager given in the manager array
where manager[i] is the direct manager of the i-th employee,
manager[headID] = -1. Also, it is guaranteed that
the subordination relationships have a tree structure.
The head of the company wants to inform all the company employees of an urgent piece of news. He will inform his direct subordinates,
and they will inform their subordinates,
and so on until all employees know about the urgent news.
The i-th employee needs informTime[i] minutes to inform all of his direct subordinates
(i.e., After informTime[i] minutes, all his direct subordinates can start spreading the news).
Return the number of minutes needed to inform all the employees about the urgent news.한 회사에 사원이 n명 있고, 각각의 사원은 0 ~ n-1의 고유한 사원번호를 가집니다.
사원들중 한명은 최고 책임자인데, 최고 책임자의 사원번호는 HeadID로 주어집니다.
manager 리스트는 각 사원을 담당하는 매니저가 누군지를 표기하는데,
i 인덱스의 번호가 p일 경우 p 사원이 i 사원의 매니저라는 뜻입니다.
informTime 의 경우는 각 사원이 모든 부사수에게 정보를 전달할때 걸리는 시간을 의미합니다.
최고 책임자가 특정한 정보를 모든 사원에게 전달하고 싶어 하는데,
정보 전달은 매니저가 자신의 부사수에게 전달하고, 또 그 부사수가 자신의 부사수에게 전달하는 식으로 이루어집니다.
모두에게 정보가 전달 될 때 까지 걸리는 시간을 리턴하세요.
예시
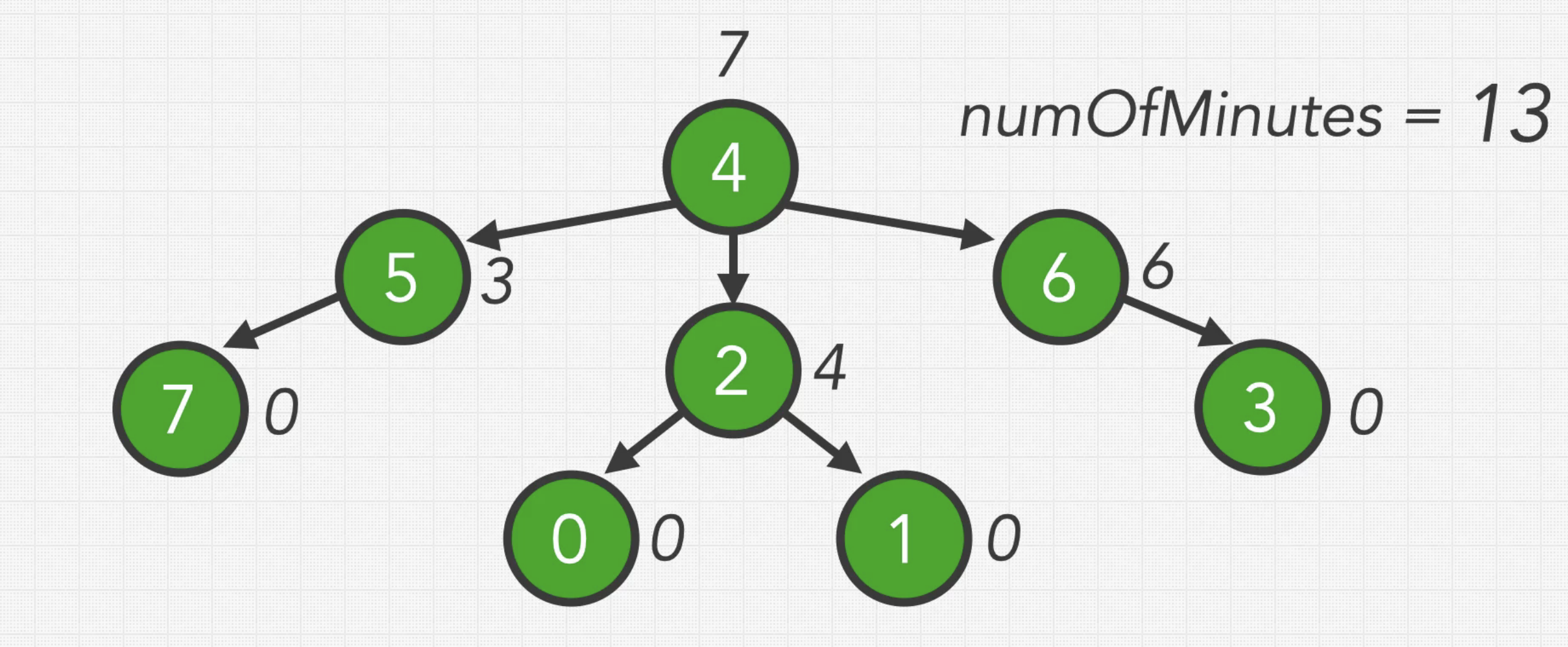
Input: n = 8
headID = 4
manager = [2, 2, 4, 6, -1, 4, 4, 5]
informTime = [0, 0, 4, 0, 7, 3, 6, 0]
Output: 13
Explanation: 전달에 제일 오래 걸리는 경우는 4 -> 6 -> 3 순서로 전달될때 13의 시간이 걸린다.제한
- 1 <= n <= 10^5
- 0 <= headID < n
- manager.length == n
- 0 <= manager[i] < n
- manager[headID] == -1
- informTime.length == n
- 0 <= informTime[i] <= 1000
- i번 사원이 부사수가 없을시 informTime[i]는 0이다.
- 매니저 <> 부사수 관계로 형성되는 그래프에서 빠지는 사원은 없다.
- 생성되는 그래프는 트리의 구조를 가지며 사이클을 절대 가지지 않는다.
풀이
매니저 <> 부사수 관계가 사이클을 형성하지 않기에 사이클이 있을 가능성은 제외할수 있으며
트리의 형태를 가진 Directed graph이기에 따로 check를 하지 않아도 중복 순회 또한 걱정 할 필요가 없으며
그로 인해 특정 노드에서 Root 노드까지 가는 경로는 단 하나가 됩니다.
Root와 Terminal 노드를 제외한 나머지 노드들의 informTime을 지금까지 걸렸던 시간으로 갱신해 나가며
Terminal에 도달시 부모 노드의 informTime의 최대값을 구하면 됩니다.
class Solution:
def numOfMinutes(self, n: int, headID: int, manager: List[int], informTime: List[int]) -> int:
maxTime = 0
graph = [list() for _ in range(n)]
for i in range(n):
if manager[i] == -1: continue
graph[manager[i]].append(i)
q = deque()
q.append(headID)
while len(q) != 0:
node = q.popleft()
for i in graph[node]:
if informTime[i] != 0:
informTime[i] += informTime[node]
q.append(i)
else:
if maxTime < informTime[node]:
maxTime = informTime[node]
return maxTime
단, 주의할점이 있는데
그래프를 형성할때, Adjacency list가 아니라 Adjacency array로 만들 경우 시간복잡도가 O(n^2)가 되어
시간 초과로 인해 문제가 풀리지 않는다.
참 독특하게 이거만 Adjacency list로 바꿔줘도 상위98%대 속도가 나오니 참고하시길.
