
문제
There are a total of numCourses courses you have to take, labeled from 0 to numCourses - 1.
You are given an array prerequisites where prerequisites[i] = [ai, bi] indicates
that you must take course bi first if you want to take course ai.
For example, the pair [0, 1], indicates that to take course 0 you have to first take course 1.
Return true if you can finish all courses. Otherwise, return false.강의 갯수 numCourses와 선행 강의 목록을 담은 prerequisites 배열이 주어진다고 가정한다.
prerequisites의 원소는 numCourse 값 n에 대해 0 ~ n-1 내의 정수 a, b에 대해
[ a, b ] 의 형태를 띄며, 이는 a강의를 듣기 위해 b 강의를 들어야 한다는 뜻이다.
전체 강의를 전부 수강할수 있을지에 대해 boolean type으로 리턴하시오.
예시
Input: numCourses = 2, prerequisites = [[1,0],[0,1]]
Output: false
Explanation: 0을 들으려 하니 1이 필요하고, 1을 들으려 하니 0이 필요하다.제한
- 1 <= numCourses <= 2000
- 0 <= prerequisites.length <= 5000
- prerequisites[i].length == 2
- 0 <= ai, bi < numCourses
- prerequsites의 강의 쌍은 전부 unique 하다.
풀이법
Topology sort
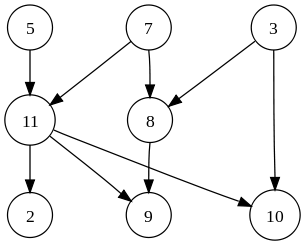
Topology sort는 위와 같은 그래프에서 노드에 진입하는 차수가 0인 노드들을 우선시 하여 정렬하는 것이다.
위 그래프의 경우 5, 7, 3 노드의 경우 진입차수가 0이기 때문에 먼저 정렬 데이터에 들어간다.
또한, 이미 정렬된 노드들은 그래프에서 빠지게 되는데, 이렇게 되면 11, 8이 진입 차수가 0이 되니
11, 9가 다음으로 정렬 데이터에 들어가고, 이후 2, 9, 8이 정렬되어
5, 7, 3, 11, 8, 2, 9, 10 으로 정렬된다.
이문제랑 무슨상관이냐?
여기서 진입차수를 그 수업을 듣기 전에 필요한 수업의 갯수라고 생각하면 이 문제를 풀기 쉽다.
진입차수가 0인, 들을수 있는 수업을 미리 큐에 집어넣고
큐에서 pop 한 다음에 남은 수업 갯수에서 1을 빼주고
이 문제를 선행으로 필요로 하는 문제들의 진입 차수를 1씩 빼주는데,
이때 진입차수가 0이 되는 수업은 드디어 들을수 있게 된 수업이기에 큐에 다시 집어넣어주는것이다.
여기서 중요한 점은 수업의 갯수를 따로 변수에 저장해놓고
큐에서 꺼낼때 마다, 즉 수업을 들을때마다 하나씩 빼 준다는 것인데.
만약 큐가 비었을때, 즉 들을수 있는 모든 수업을 들었을때 이 남은 수업이 0이 아니라면 False를 리턴하고
남은 수업의 갯수가 0이면 모든 수업을 들은 것이기에 True를 리턴하는 것이다.
이를 위해 그래프와 진입 차수를 표기하기 위한 class를 하나 더 구현하였다.
class Node:
def __init__(self):
self.connected = []
self.inbound = 0
class Solution:
def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:
graph = [Node() for _ in range(numCourses)]
left = numCourses
for i in prerequisites:
graph[i[1]].connected.append(i[0])
graph[i[0]].inbound += 1
q = deque()
for node in graph:
if node.inbound == 0: q.append(node)
while len(q) != 0:
node: Node = q.popleft()
left -= 1
for c in node.connected:
graph[c].inbound -= 1
if graph[c].inbound == 0:
q.append(graph[c])
if left == 0: return True
else: return False