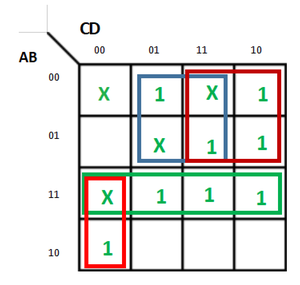
Switching function의 최소 형태
- Function의 비용은 AND/OR과 같은 게이트를 덜 쓰고 입력을 덜 받는 형태이다.
- 카르노 맵을 통해 AND/OR 게이트로 만드는 최소-비용 회로의 구성이 가능하다.
- Minimum sum-of-product 혹은 Minimum product-of-sum의 형태를 구할수 있다.
Minimum sum-of-product
- 항의 갯수가 최소이다.
- 동일한 항의 갯수에 대해선 각각의 항이 최소한의 변수를 가진다.
- 한가지 Function 에 대해 여러개의 Minimum sum-of-product가 있을수 있다.
카르노 맵
- 기본적으로 여러개의 minterm이나 maxterm을 하나로 묶는것
.는 없어지는 부분을 의미한다.
- 두개의 term에 대해 1비트가 complement관계일시 이를 합치고 complement인 literal을 없앨수 있다.
2/3 변수 카르노 맵
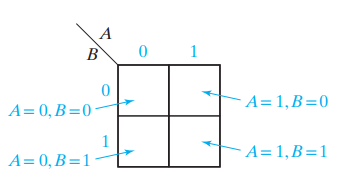
2-변수 카르노맵
-
각각의 cell에 truth table의 값을 넣는다.
-
이후 개의 직사각형으로 1을 묶어준다.
-
이후 묶여진 직사각형 범위에서 값이 바뀌지 않는 것을 기준으로 직사각형 하나마다 minterm을 만든다.
-
왼쪽 위 항은 A=0이고 B=0일때의 output을 의미한다.
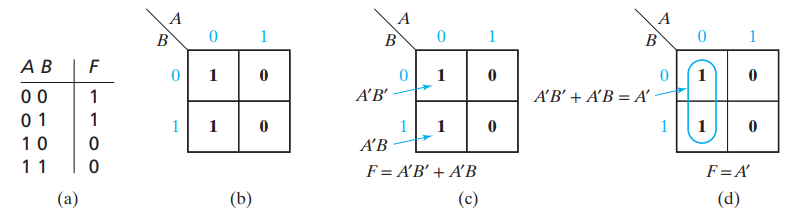
줄이는 법
- 1을 output으로 가지는 cell을 직사각형으로 개 묶고, 두 cell이 동일한 input을 가지는것에 한정해 minterm으로 바꾼다.
- 위 경우 B는 0과 1의 경우지만, 두 경우 A는 0이기 때문에 이 된다.
- 최대한 크게 합칠수록 term을 더 줄일수 있다.
3-변수 카르노맵

- 하지만 BC의 순서가 00, 01, 11, 10인데 이는 비트가 하나씩만 바뀌도록 하기 위함이다.
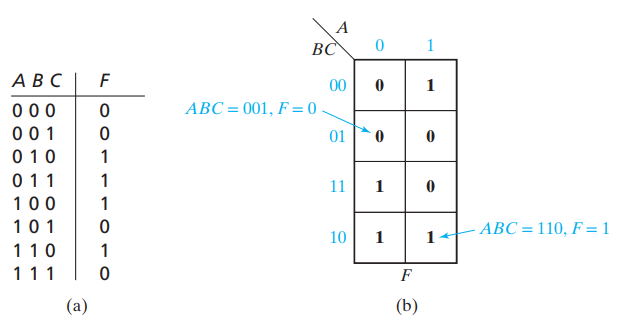
- 카르노맵은 앞뒤 좌우가 연결되어있다고 가정하고, 각각의 사각형이 겹쳐도 된다.


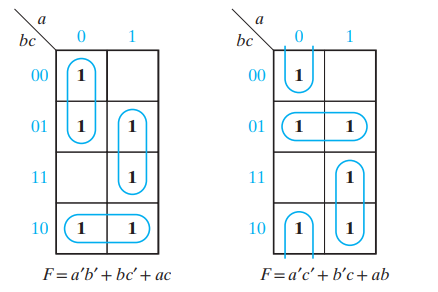
4변수 카르노 맵
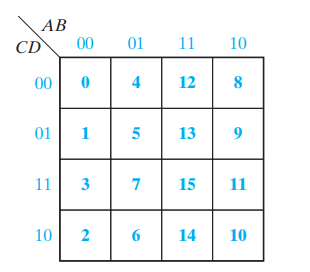
- 3변수와 동일하되 4 * 4의 형태를 가진다.

최소 표현 찾아내기
- minterm 표현을 받았을때 바로 카르노 맵을 그릴수 있다.
카르노 맵에서의 Don't care term
- 해당하는 minterm에 X 표시하기.
- 직사각형에 포함되거나 포함되지 않을수 있다.
- 꼭 포함되어야 하진 않는다.
Minimum product of sum
바로 찾기
- 0이 되는 부분을 으로 묶어서 찾는다.
- 0이 되도록 maxterm을 찾으면 된다.
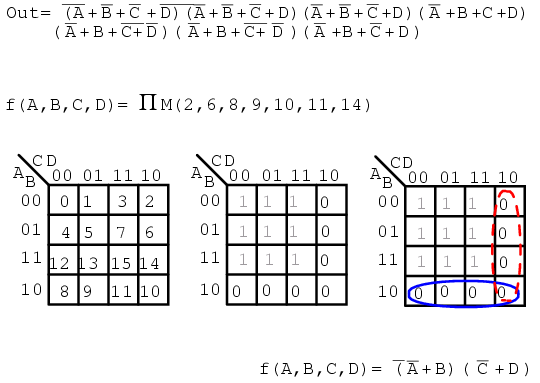
Complement
- 의 minimum sum of product 를 찾기
- 찾아진 sum of product에 complement를 취해 드모르간 법칙을 이용, 이를 product of sum으로 변환한다.
sum of product 나 product of sum 형태 중 gate를 적게 쓰는쪽(항의 갯수가 적다) 이 더 좋다.
Implicant of F
- 카르노맵에서 이거나 이 개가 묶인 직사각형의 그룹
- 개의 로 이루어질수 있다.
Prime Implicant
- 더이상 다른 Implicant와 합쳐질수 없는 Implicant이다.
- 만들수 있는 가장 큰 Implicant들중 하나이다.
특정 minterm이 오직 특정한 1개의 prime implicant에 의해 정의 될시, 그 prime implicant는 essential 하다.
Essential Prime Implicant : EPI
반드시 포함되는 Implicant
5변수 카르노 맵
- 대각선을 이용해 표현한다!
- 대각선 기준 왼쪽이 1, 오른쪽이 0이다.
- 대각선에는 A / 첫번째 Literal 이 들어간다.'
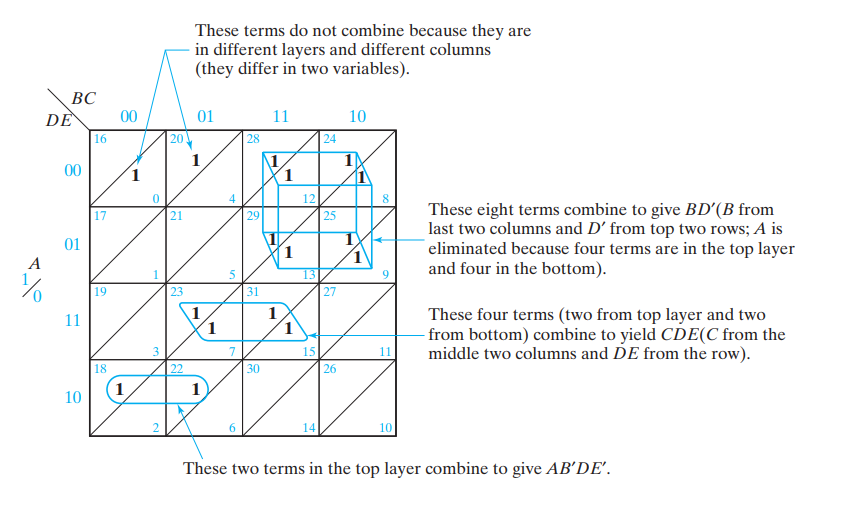
다른 카르노맵의 용도
와 같은 minterm expansion을 쉽게 줄여 표현할수 있다.


