논리회로 CH6. 카르노맵, More

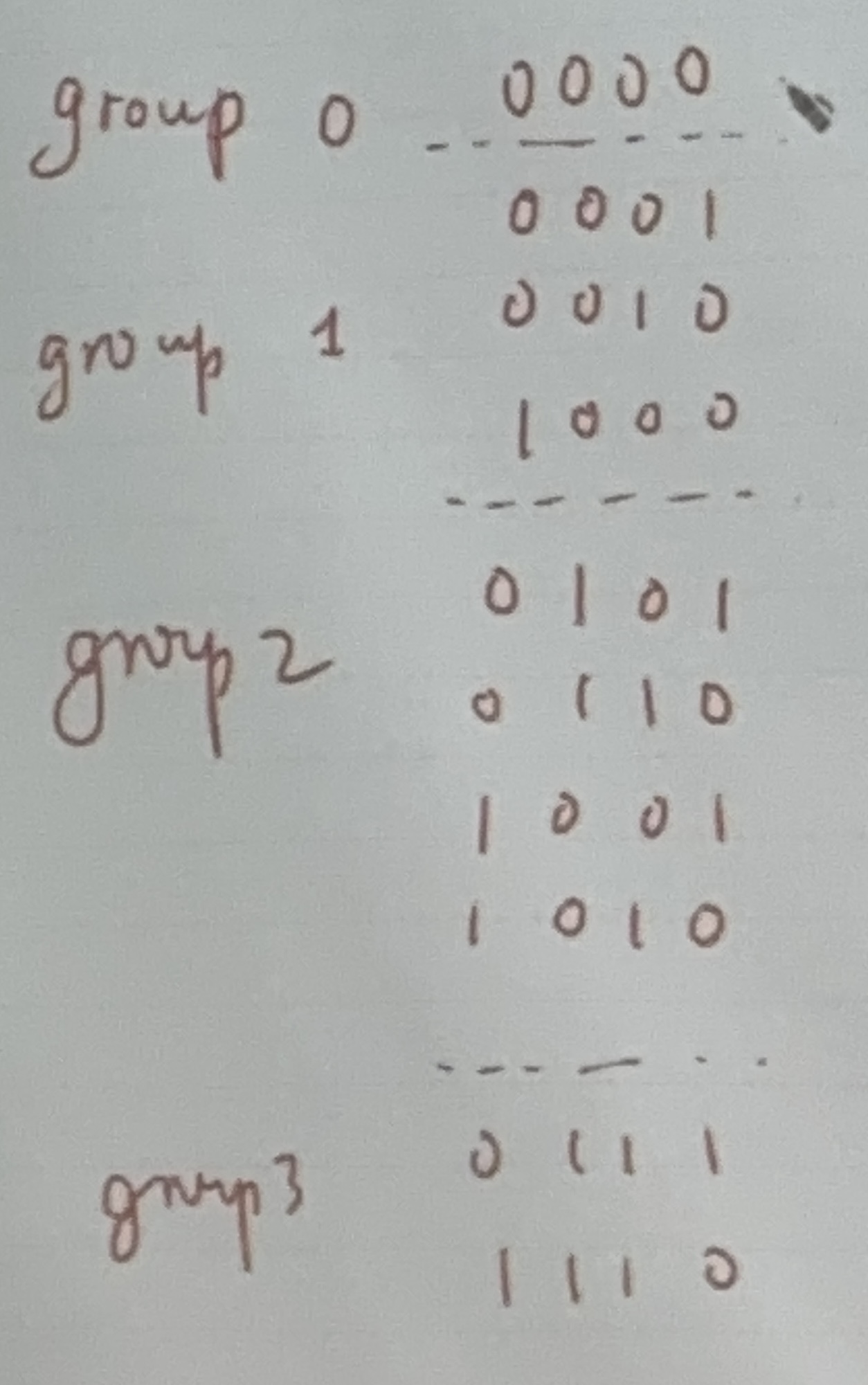
Quine McCluskey Method

Minimum sum of product expression을 찾아보자.

5변수 이상에서의 실용적 방식

예시

$f(a, b, c, d) = \Sigma m(0, 1, 2, 5, 6, 7, 8, 9, 10, 14)$ 의 Minimum SOP expression 을 찾아보자

• 모든 가능한 minterm들의 쌍이 비교되어야 하는데, 이를 쉽게 하기 위해 minterm number 내의 숫자들이 1을 가진 갯수로 그룹을 만든다.

1. 결과적으로 아래와 같은 minterm의 리스트가 만들어진다.

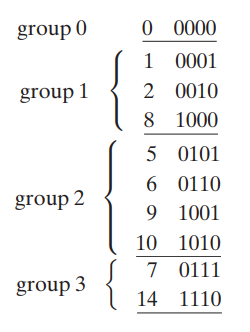
group n : n개의 1을 가지고 있는 minterm

2. 인접한 그룹끼리 비교하여 비트가 단 1개만 다른 경우 각 쌍에 옆에 체크해두고 따로 오른쪽에 가능한 쌍을 전부 적어둔다.
   • 적을때 비트가 다른 부분은 "-"로 표기하고 나머진 그대로 표기한다.

3. 이 과정을 더이상 비트가 1 차이나는 경우가 없을때까지 반복한다, 또한 minterm의 표기가 중복되는 경우는 제거한다.
   -00- 2개가 중복되어 하나를 삭제한것을 볼수 있다

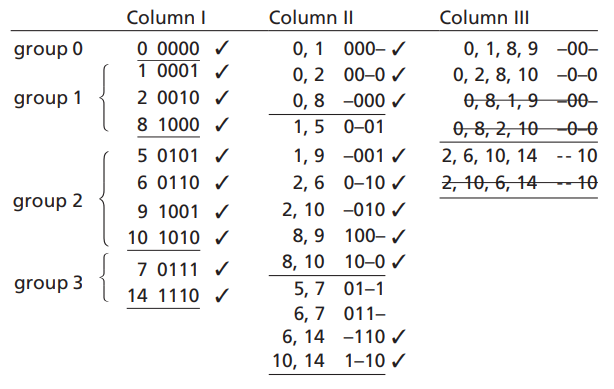
완성시 체크되어있지 않은 minterm들이 바로 SOP를 이루는 Prime Implicant이다!
체크되지 않은것 == 다른 minterm과 합쳐질수 없음 == Prime Implicant

• 하지만 아직 Minimum하진 않다.

---

Prime Implicant Chart

• 두번째 과정

1. 각 Prime Implicant에 대해 자신을 포함하는 minterm을 표기하는 차트를 그린다.

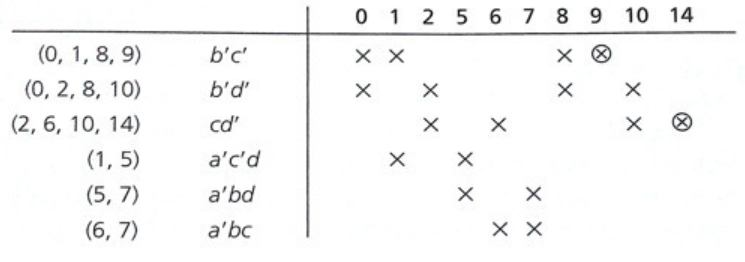
$b'c'$는 카르노맵에서 0, 1, 8, 9번 minterm이 포함된다.

2. 작성 후 Column을 살펴 보았을때 X가 하나밖에 없는 경우, 그 X가 포함된 minterm은 Essential Prime Implicant이다.
   • 즉, 절대 빠져선 안되는 minterm이다.
   • 9 / 14번 minterm을 커버 할수 있는 Prime Implicant는 각각 하나씩 밖에 없다는 뜻!
3. 이 Essential Prime Implicant인 minterm들에 대해 가로줄을 그어준 뒤, X를 만날때마다 세로줄을 그어준다.
   Essential Prime Implicant로 이미 Cover 되는 minterm들을 제거

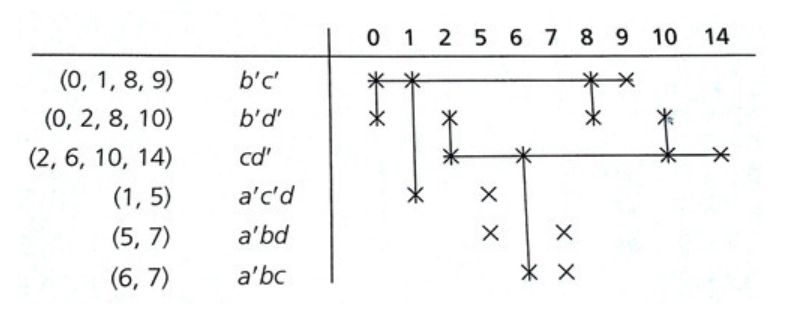
• 여기서 선택되지 않은 X를 가진 항을 잘 선택해 모든 X가 cover되도록 하는 쌍을 구한다.
  • 여기선 $a'c'b, a'bd, a'bc$ 이 세개중 하나를 선택하는데,
    $a'bd$를 선택시 남은 X가 전부 커버 된다.
• Essential Prime Implicant가 없는 경우, 최소한을 선택해 전부 Cover할수 있는 경우를 찾는다.

4. 골라진 minterm과 Essential Prime Implicant 들로 Minimum SOP를 구성한다.

• $a'bd + b'c' + cd'$ 가 완성된 Minimum SOP Expression

여러개의 Minimum SOP Expression이 있을수 있다!!!

---

Patrick's Method

• Essential Prime Implicant는 $P_i$에서 제외해야 한다!!!!!!!
• Prime Implicant Chart로부터 모든 가능한 Minimum SOP expression을 찾는다.

1. Prime Implicant Chart의 Row에 $P_1$부터 $P_6$까지의 이름을 매긴다.

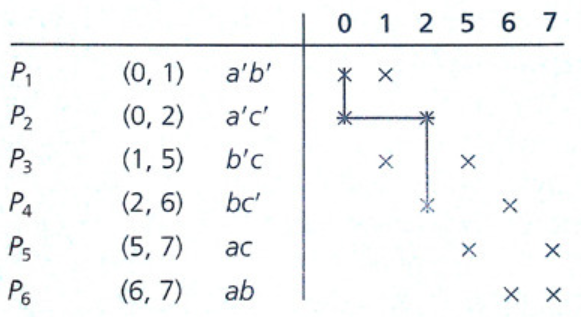
2. 모든 minterm이 cover되었을때 항상 1이 되는 논리함수 P를 만든다.
   $P_i$는 자신이 minimum solution에 포함시 1의 값을 가진다.

3. Column에서 X가 있는 minterm을 POS 형식으로 묶어준다.
   
   0 minterm은 1번 혹은 2번이 선택되어야 Cover가 된다.
   1 minterm은 1번 혹은 3번이 선택되어야 Cover가 된다.
   ...

4. 위 식을 정리하면 가장 변수의 갯수가 적은 항이 나오는데, 이들이 이루는 minterm과 Essential Prime Implicant들로 Minimum SOP expression이 구성된다.

1, 4, 5 혹은 2, 3, 6
$f(a, b, c) = \Sigma m(1, 4, 5)$
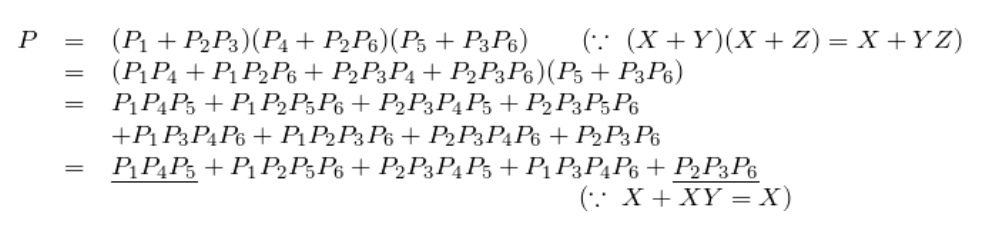
$f(a, b, c) = \Sigma m(2, 3, 6)$

---

Incompletely Specified Function의 경우

Dont care가 포함된 경우는

• 첫단계엔 포함되나 Prime Implicant Chart에서 제외된다.

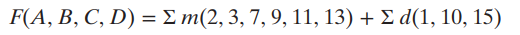
1, 10, 15 포함

1, 10, 15 미포함