논리회로 Ch4. Maxterm and Minterm

4.1 영문장을 Boolean Equation으로 변환하기

단일출력 조합스위칭 회로 디자인 하는법

1. 원하는 동작을 하는 Switching Function을 찾는다.
2. 그 Function에 맞는 단순화된 Algebric expression을 찾는다.
3. 단순화된 Function을 Logic element로 표현한다.

영문장을 Boolean equation으로

• 문장을 구문으로 나누고 이를 Boolean variable로 치환한다.
• True/False의 경우를 가지는 구문은 Boolean variable로 치환할수 있다.

EX : Marie watchces TV
     True  => Marie watches TV
     False => Marie doesn't watch TV

• 사용 예시

 Mary watches TV if it is Monday night and she has finished her homework. 
 Mary watches TV => Result
 it is Monday night and she has finished her homework. => Cause
 --------------------
 Mary watches TV = F
 It is Monday Night = A
 She has finished her homework = B
 --------------------

$F = A \cdot B$

---

4.2 Combinational Logic Design Using Truth Table

• 세개의 Input과 1개의 Output을 가지는 Switching circuit이 있다고 가정한다.

• Switching Circuit의 Logic gate에서의 모습과 Truth table이 다음과 같다고 한다.
  

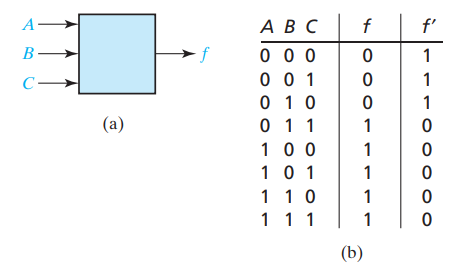
• f가 1이될때 ABC의 조합에 대해 살펴보면

A'BC는 A,B,C가 각각 0,1,1일때만 1이 된다.
ABC는 A,B,C가 각각 1,1,1일때만 1이 된다.
즉, Truth table에서의 한개의 Row의 경우만 Covert하는 Product Form이 되는 것이다.

• f가 1일때 세 변수의 곱이 1이되게 하는 보수 혹은 일반 변수의 곱의 쌍들을 전부 찾아 sum of product form으로 표현시 아래와 같게 된다.

$f = A'BC + AB'C' + AB'C + ABC' + ABC$

• 기타 A, B, C 혹은 그의 보수의 의 곱은 결과적으로 F가 0이되는 쌍밖에 없기 때문에 이 식에 없다.

• 위식은 간략화가 가능하다.

$f = A′BC + AB′ + AB = A′BC + A = A + BC$

• 결론적으로 구해지는 circuit은 다음과 같다.
  

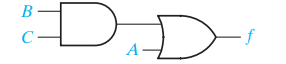
반대로

• 0이 되는 경우만 찾아서 식을 만들수도 있는데,

$A+B+C$의 경우 A, B, C가 전부 0이여야 결과가 0이된다.

• 같은식으로 전부 찾아 나온 합들을 곱해준다.

• 이로 인해 생긴 결과는 곱을 이루는 항이 하나라도 0이 되지 않는 이상 결과는 1이 된다.

• 즉 f가 0이 되는 쌍이 하나라도 들어왔을때만 결과가 0이 되게 된다.

$f = (A + B + C)(A + B + C')(A + B' + C)$

이 또한 $A + BC$로 줄일수 있다.

---

4.3 Minterm / Maxterm

Minterm

• minterm of n variable
  • product of n literals, each variable appears exactly once with complemented or true form
  • EX. $AB'C$
    $AB$ is not a minterm
• maxterm of n variable
  • sum of n literals, each variable appears exactly once with complemented or true form
  • EX. $A+B'+C$
    $A+B'$ is not a maxterm

• 각각의 minterm은 $m_0$, $m_1$과 같이 불리기도 한다.

• 아래는 불리는 방식에 대해 적은것이다.

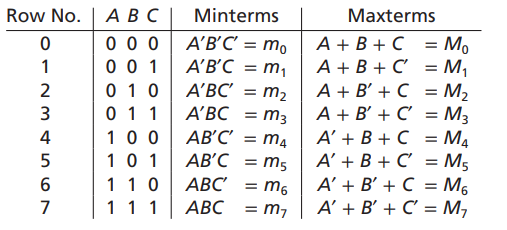
• minterm의 경우 계산식이 1이 되도록 하며, Maxterm의 경우 계산식이 0이 되도록 한다.
• 숫자 붙히는것은 0부터 시작한다.
• 변수의 개수 n에 때라 $0 \sim 2^n-1$개의

---

Minterm expansion

• minterm 의 합

$f = A'BC + AB'C'+ AB'C + ABC' + ABC$ 의 경우

$f(A, B, C) = m_3 + m_4 + m_5 + m_6 + m_7$ 로 표현될수 있다.

=> $f(A, B, C) = \Sigma m(3, 4, 5, 6, 7)$

• Summation m 3, 4, 5, 6, 7

---

Maxter expansion

• maxterm 의 곱

$f = (A + B + C)(A + B + C')(A + B' + C)$ 의 경우

$f(A, B, C) = M_0 \cdot M_1 \cdot M_2$ 로 표현될수 있다.

=> $f(A, B, C) = \Pi M(0, 1, 2)$

Multiplication M 0, 1, 2

예시

$f(a, b, c, d) = a'(b'+d') + acd'$ 를 minterm expansion으로

$= a'b + a'd + acd'$

가능한 모든 경우의 수를 적는다.

$= a'b'(c+c') + a'd(b+b') + acd'(b+b')$

첫항의 결과엔 d가 없으니까 (d+d')를 또 곱하고
두번째항은 c가 없으니(c+c')을 또 곱해주면 된다

---

4.4 General Minterm and Maxterm Expansion

General expansion of minterm

• 위 식에서 minterm을 Formal 하게 표현시

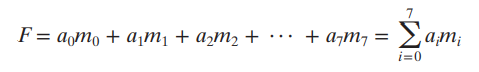
General expansion of maxterm

• 위 식에서 maxterm을 Formal 하게 표현시

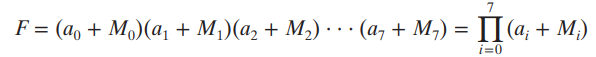
$a_i$가 1이되면 그 덧셈항의 결과는 무조건 1이 되기에,덧셈항 내부의 결과가 0이 되어야하는 Maxterm의 특성상 의미 없는 항이 된다.

결과

$F = minterm = maxterm$

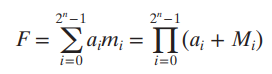
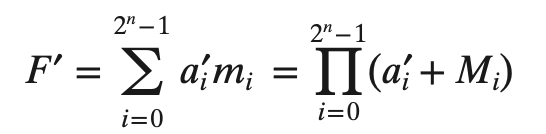
• F의 보수에 대해선 $a_i$를 보수로 주면 된다.

+

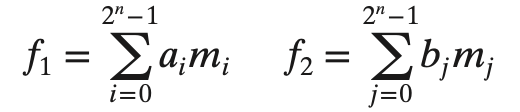
• 일때

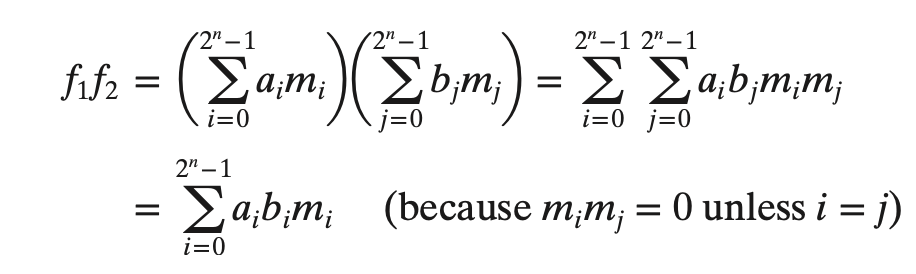
• 서로의 AND은 아래와 같이 되는데
• $a_i \times b_i$ 가 1이 되는것만 남는 셈이다.

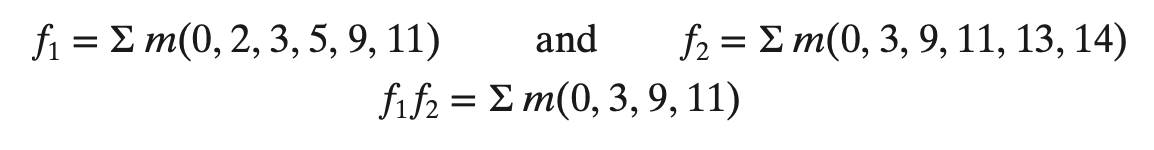
• 이로 인해 위 식이 성립한다.
• 두쪽에 겹치는것만 남게된다.

---

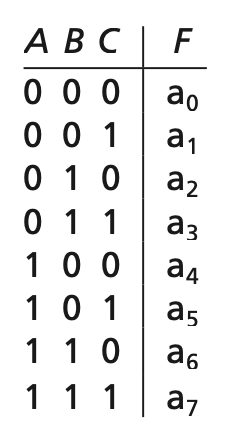
4.5 Incompletely Specified Function

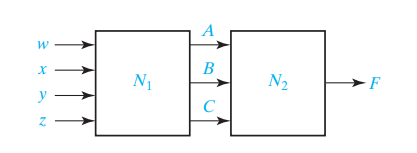
• 위와 같은 논리회로에서 $N_2$의 진리표가 다음과 같을때
• $N_1$의 결과인 $A, B, C$가 가능한 모든 경우의 수를 커버하지 않을수 있습니다.
• 예를 들어 A가 0이고 B가 0이고 C가 1인 Output은 발생하지 않는다.
• 즉 $N_2$에는 $A = 0, B = 1, C = 1$인 Input은 절대로 들어올수 없다.

• 그럴 경우 Output을 X로 표기하며
• 이를 Don't care term이라 부릅니다.

• Don't care term 이 1개 이상 있을시 Incompletely spedified function 이라 부릅니다.
• Don't care term이 위치하는 Input에 대해선 어떤 Output이 나올지 자유롭게 가정할수 있습니다.
• 또한 가정을 이용해 Logic expression을 간소화 하는데 도움을 줄수 있습니다.

Don't care 표기

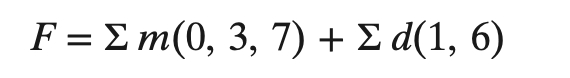
• minterm 소문자
  
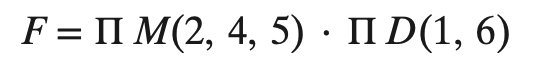
• maxterm 대문자

---

4.6 Examples of Truth table construction

• 2bit 숫자를 2개 더하는 Logic gate의 Truth table

• 이 경우 minterm으로 표시하려면 각각의 출력 변수에 대해 표시하면 된다.

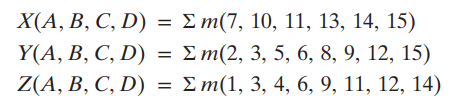
1 Bit adder / Half adder

• 1 Bit + 1 Bit를 계산한다.

a + b

a	b	carry	sum
0	0	0	0
0	1	0	1
1	0	0	1
1	1	1	0

• carry : $a \cdot b$
• sum : $a \oplus b$

n Bit adder

• n*2개의 입력을 받아 n+1개의 출력이 나온다.

---

4.7 Design of Binary Adder and Substractor

• 1개의 Full adder는 $A, B, Carry_{in}$를 받아 $Carry_{out}$와 $Sum$의 결과를 준다.

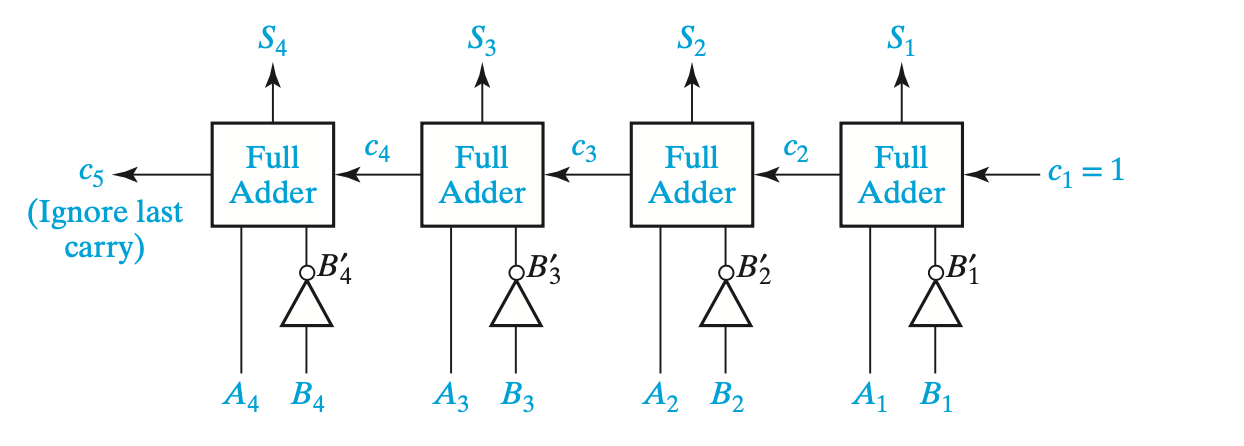
• 그것을 4개 붙힌 4-Bit 병렬 가산기의 경우 다음과 같다.

• 아래 가산기는 Riffle Carry Adder로도 불리며, 앞의 Full adder가 뒤의 Full adder의 Carry값이 계산 될 때 까지 기다려야 한다는 특징이 있다.

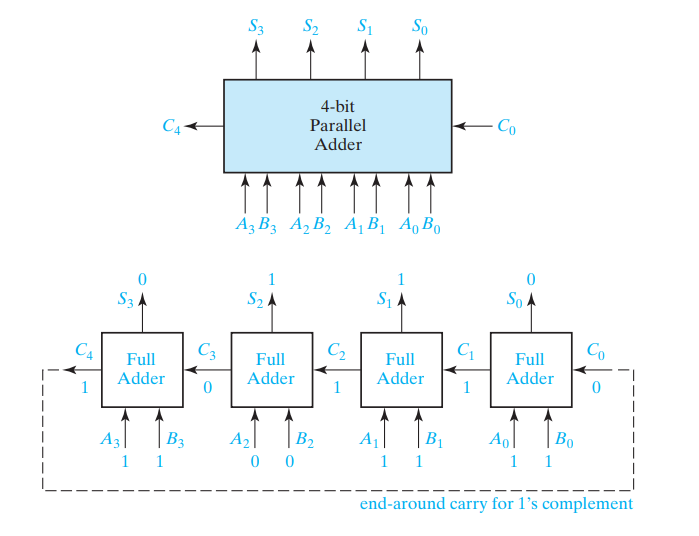
Carry가 Sum으로 가는것은 1의 보수 연산시 필요한 과정.

• Ripple carry adder - carry를 왼쪽으로 더하며 계산

• 결과는 $S_3S_2S_1S_0$ 이다.

• Full adder의 진리표는 다음과 같다.

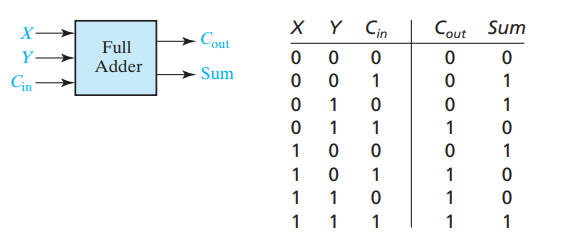
• 또한 각각 변수의 Boolean Expression은 다음과 같다.

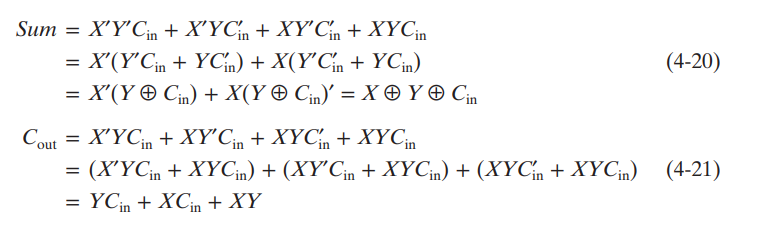
Sum의 경우 1의 갯수가 홀수면 1이기에 XOR을 쓴다고도 볼수 있다

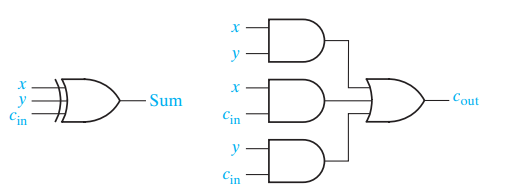
• 이를 Logic gate로 적으면 다음과 같다.

---

4-bit Subtractor

• 2의 보수 표기법을 통해 음수를 표현한다.
• A-B 는 A+(-B)로 표현할수 있다.
• 4-3 = 4+(-3) = 4 + (3의 2의 보수 표현)
• 즉 뺄셈을 덧셈을 위한 논리회로로 구현할수 있다!

여기 $C_0$ 자리에 2의 보수를 위한 1 더하기를 해줄수 있다

Subtractor

• x - y = d
• 최 우측 borrow는 0이여야 한다.
  
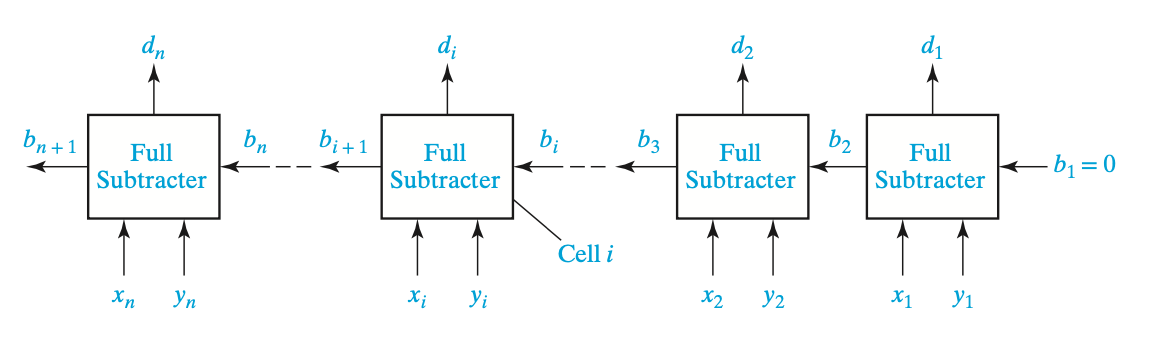
  생긴것 자체는 Parallel full adder와 동일

Full subtractor의 truth table

x - y - b

• minterm으로 표현 가능

Borrow

• 앞 자리 숫자에서 뺄셈을 했을때 빌림이 필요했다는것을 상위 자릿수에 알려주기 위함.

---

Gate delay

• 논리 Gate를 통과하는데 걸리는 시간
• 일종의 비용
• 줄일수 있으면 줄이는것이 좋다.

Full adder - 2 Gate delay

4 bit Parallel adder - 8 Gate delay

Carry Look-Ahead Adder

• Carry가 빨리 결정되어 Gate delay를 줄인다.

Carry

• $C_{i+1} = A_iB_i * A_iC_i + B_iC_i$
  = $A_iB_i + C_i(A_i+B_i)$
  = $A_iB_i + C_i(A_i \oplus B_i)$
  = $G_i + C_i(P_i)$
  G = Generator, P = Propagator

즉 아래 P, G를 통해

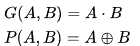
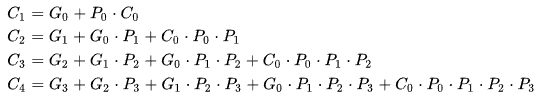
Carry를 바로 예측 가능하다!

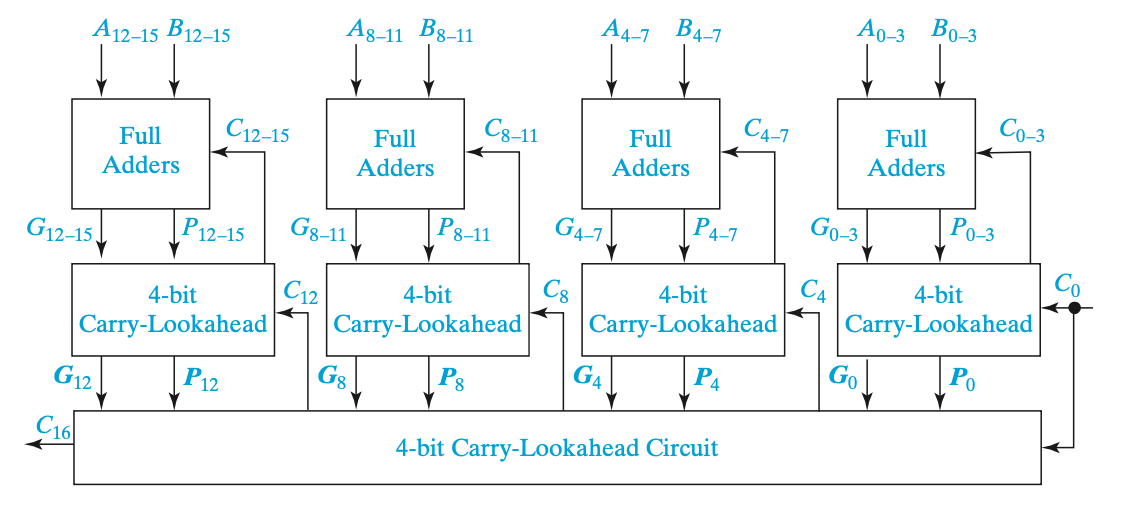
• 4개의 carry를 input의 조합으로 표현할수 있다.
• 게이트 수는 많지만 Gate delay를 줄일수 있다.