Terminology
- Gate Input : Gate에 들어가는 입력의 총 갯수, NOT은 포함하지 않는다,
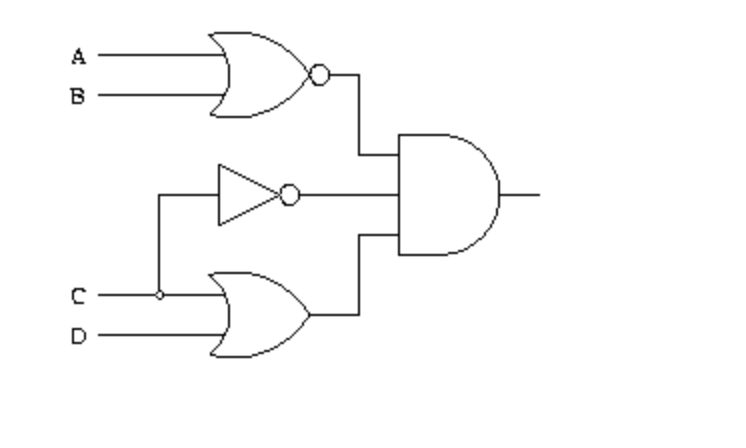
- 2 + 2 + 3 = 7 이다.
2 Level logic 을 3 Level logic 으로 변환
- Gate Input을 줄일수 있다.
- Distributive law / Elimination law 등을 이용해 변환 한다.
NAND / NOR
NAND = AND + NOT

NOR = OR + NOR
AND / OR 을 만드는데 필요한 트랜지스터의 수가 NAND / NOR을 구성하는것보다 많이 필요하다.
이들을 대신 사용하면 적은 비용이 든다는 것.
- Set of Operation이 Functionally complete >> 그것으로 모든 Boolean expression의 구현이 가능하다.
- {AND, OR, NOT} 은 Functionally complete 하다!
- 위 셋을 구현 가능한 Set은 모두 Functionally complete하게 된다.
- {NAND} 또한 Functionally Complete 하다.
NAND 이용하기 / Functionally complete의 증명
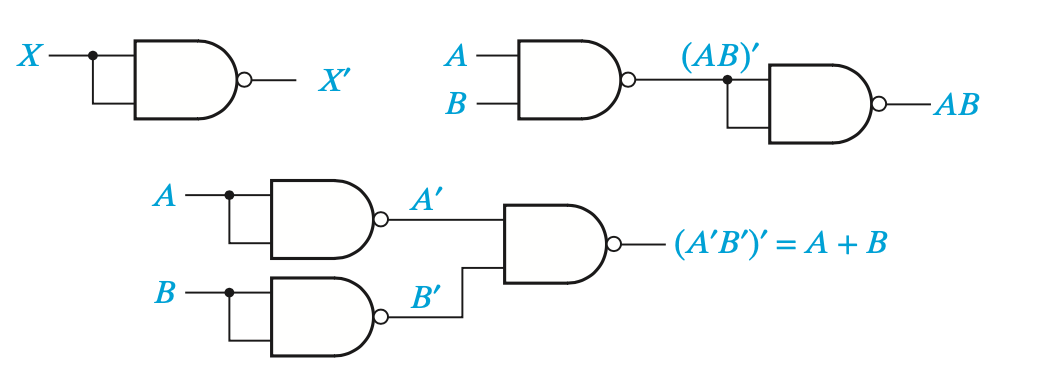
- 같은 입력 두개를 넣어 NOT으로 사용하기.
- NAND이후 NOT을 해서 AND로 사용하기.
- 각각 입력에 NOT을 해주고 NAND를 해서 사실상 OR과 같게 사용하기.
NOR 또한 가능하다!
NAND와 NOR 활용 2 레벨 회로
드 모르간 원리를 적극 활용한다!
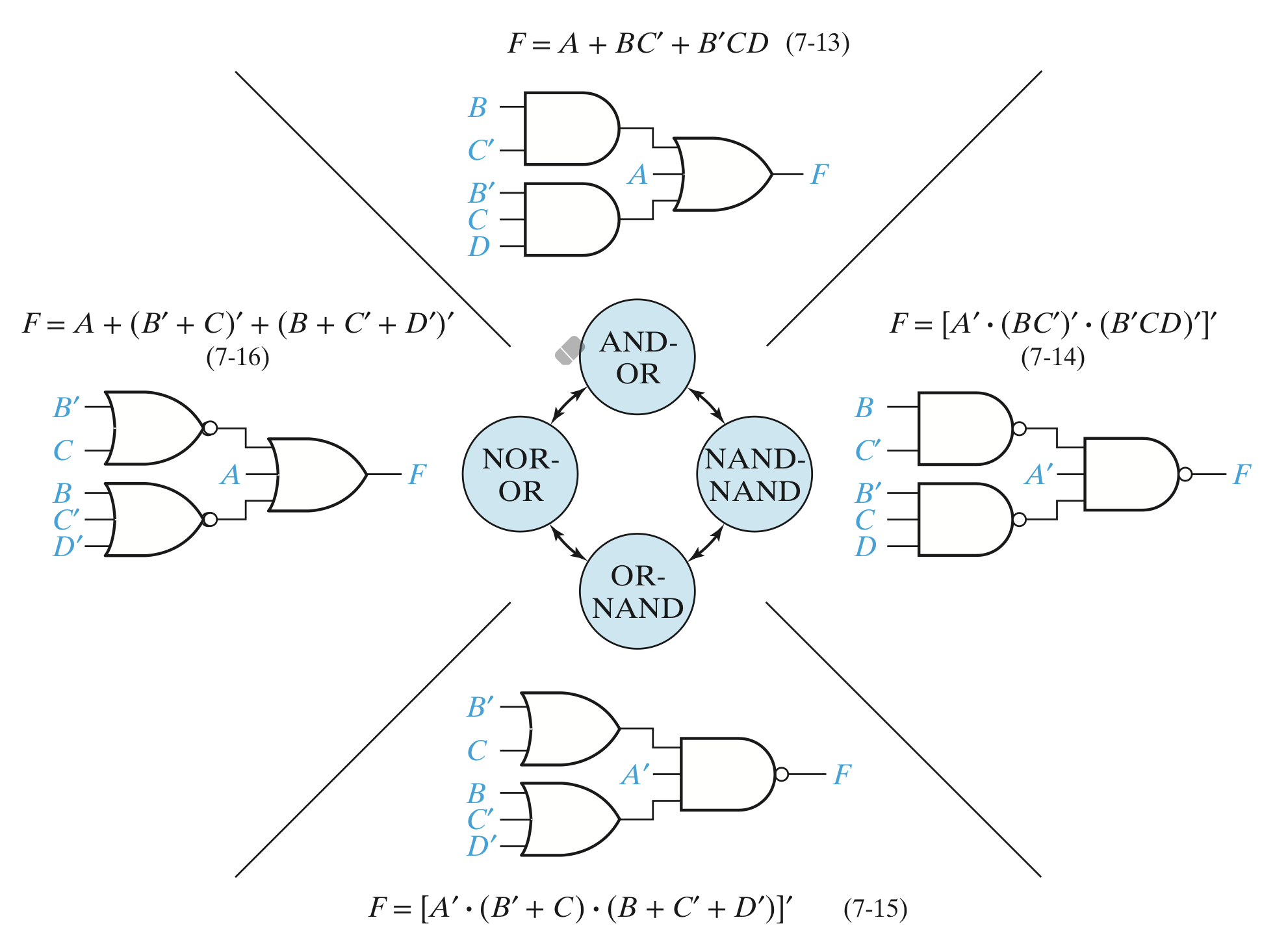
- 단일 OR / AND만 바꿀시 Input에 전부 NOT이 필요하다.
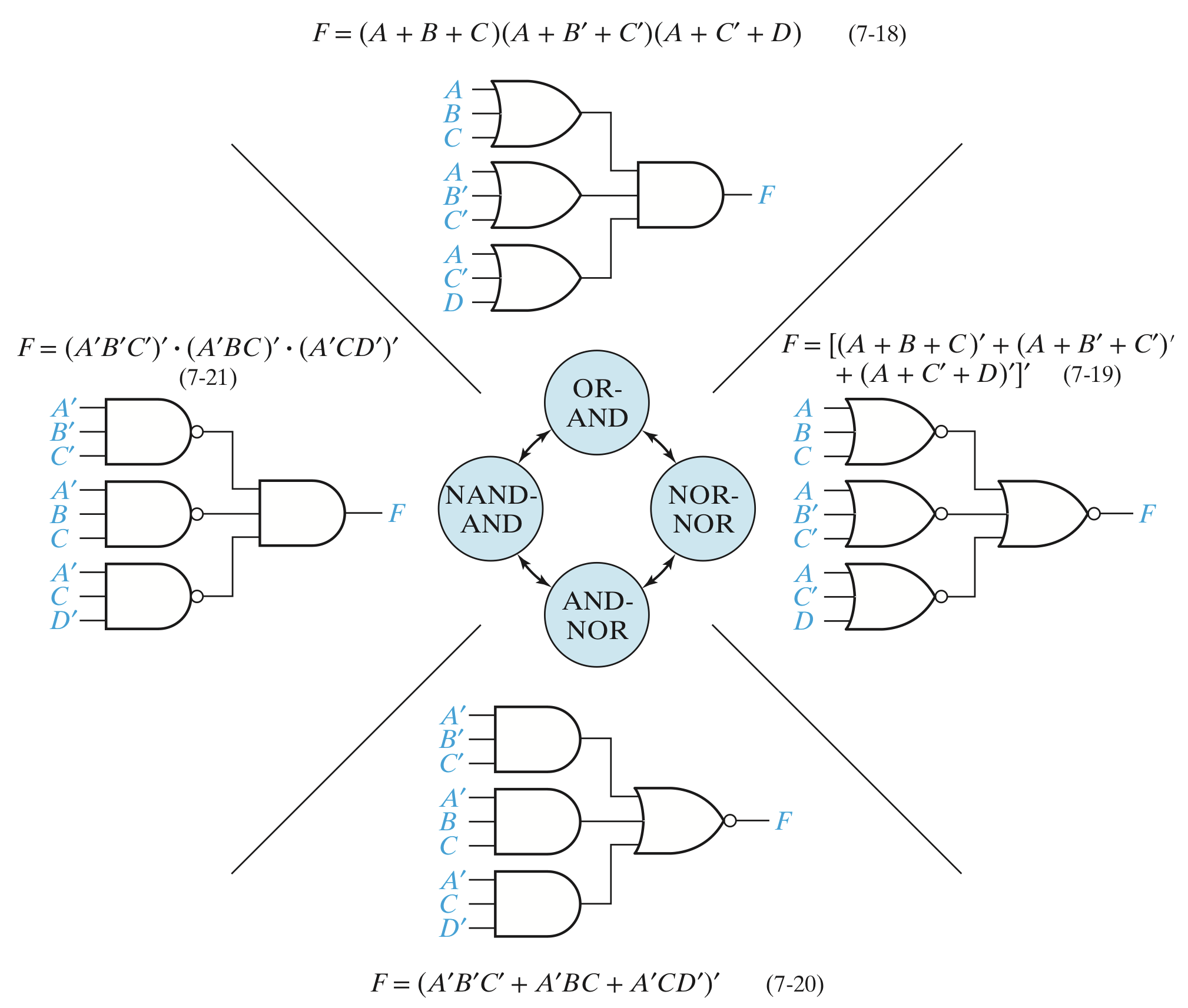
- AND 게이트는 Input에 모두 NOT이 붙은 NOR 게이트와 같다.
- OR 게이트는 Input에 모두 NOT이 붙은 NAND 게이트와 같다.
NAND와 NOR 활용 N 레벨 회로
- 동일한 방식을 이용한다.
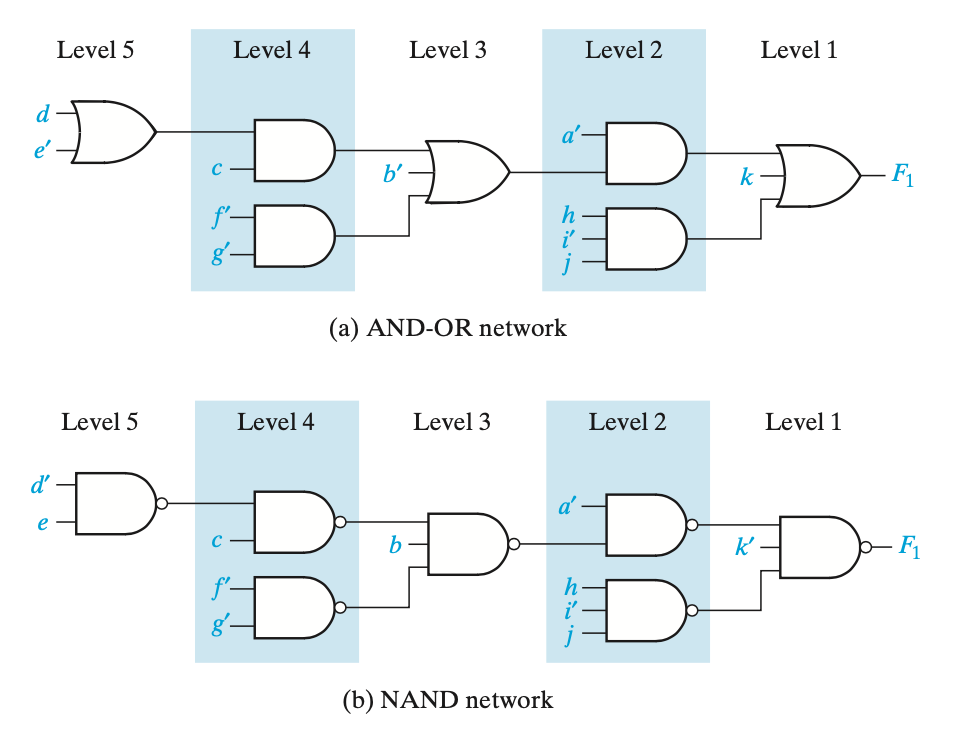
회로의 레벨 : 입력이 거치는 게이트 수의 최댓값
출력이 여러개인 회로의 구현
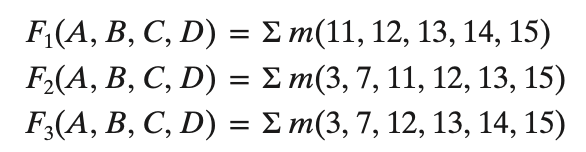
- 입력에 출력이 인 경우
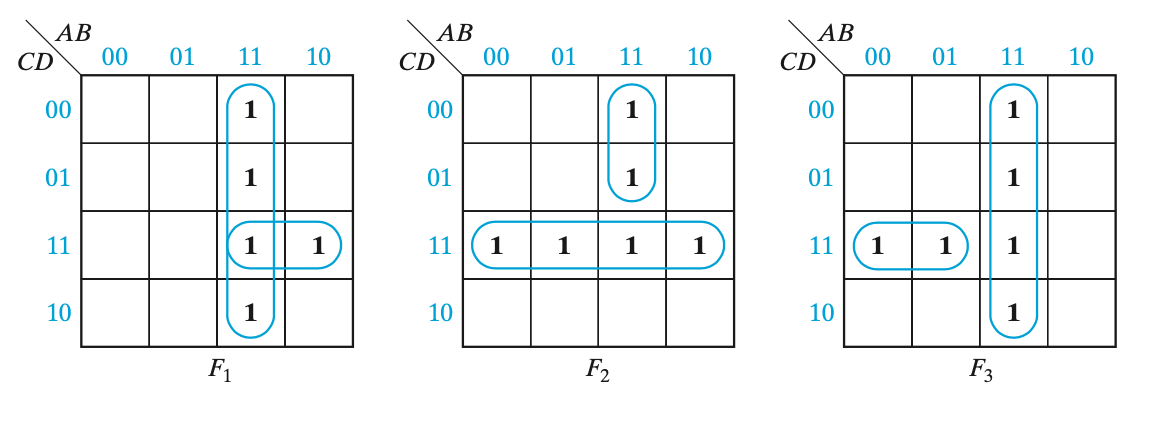
- 카르노 맵으로 표기한 결과
- 둘 다에 가 포함되기에, 둘에 대해 이를 같이 사용할수 있다.
- 에 있는 는 와 같으며, 각각 에 이미 있어 같이 사용할수 있다.
다른것들과 적절히 조합해 게이트의 수를 줄이는 것
공통항을 이용해 전체 회로를 축소한다고 표현
