논리회로 Ch3. Boolean Algebra More

3.1 Multiplying Out and Factoring Expressions

• 일단 이 두 식은 Distributive Law에 의해 성립한다.

$X(Y + Z) = XY + XZ$

$(X + Y)(X + Z) = X + YZ$

• 합의 곱의 각 첫 항이 서로의 보수일 경우 아래와 같은 공식이 성립한다.
  

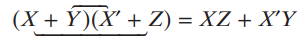
• 곱의 합에도 사용 가능하다.
  

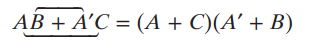
• 형태만 비슷하다면 전부 사용 가능하다. 물론 이 경우 우측항을 Commutative law로 서로 바꿀 경우 형태가 같아진다.
  

• 더 복잡한 예시
  

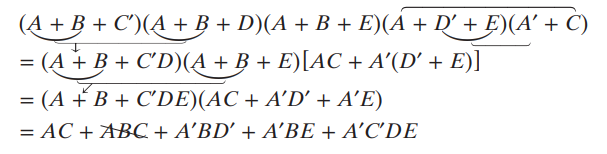
3.2 Exclusive-OR, Equivalence Operation

Exclusive OR / XOR

• XOR의 진리표는 다음과 같다.
  
• 두 변수가 다를 경우에만 1이 된다.

• 이를 Boolean Expression 으로 표현하는 방법
  
• XOR은 Logic gate에서는 다음과 같이 표기한다.
  
• XOR에 적용되는 법칙은 다음과 같다.
  
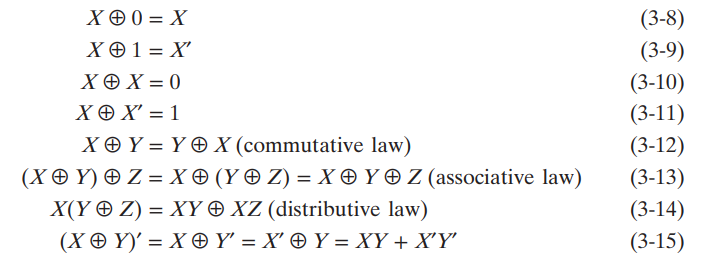
• 여러 변수를 XOR 연산 할 경우, 변수들의 1의 갯수가 홀수가 되어야 결과가 1이 된다.
  • $A \oplus B \oplus C$ 의 경우 A, B, C 중 1의 갯수가 홀수가 되어야 결과가 1이된다.
  • 이 법칙을 활용해 Parity bit를 계산할때 사용하기도 한다.

Equivalence opeerator ≡

책마다 표기법이 다른데 어떤책은 =으로 표기하기도 한다.

• Equivalence Operator의 진리표는 다음과 같다.
  
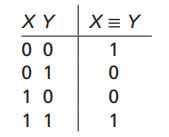
• 두 변수가 같은 경우에만 1이 된다.

• 이를 Boolean Expression으로 표기하기 위한 방법
  
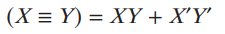
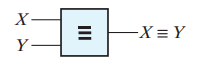
• Logic gate에서 Equivalence operator는 다음과 같이 표기한다.
  

둘 사이 관계

• $\oplus$와 $\equiv$ 는 서로 보수관계이다.

$(X \oplus Y)' = (X \equiv Y)$

• 이로인해 Equivalence operator는 종종 exclusive-NOR 으로도 불리며 아래와 같이 표기된다.
  

---

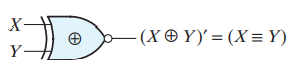
3.3 Consensus Theorem

• Boolean expression에서 Redundant한 표현을 제거하는데 사용된다.

• 만약 $ab + ac' + bc$와 같은 식이 있을시,
  ab에 대해 a와 b가 c와 c'으로 곱해진 항이 있기 때문에
  이는 소거 가능하다.

예시 : $XY + X'Z + YZ$에서 $YZ$를 소거해 $XY + X'Z$ 로 표현함.

또다른 예시
b'c 와 ab가 소거되었다.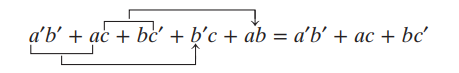

3.4 Algebric simplification of Switching Expression

• 여러 표현을 하나로 묶어 규칙을 사용해 간략화 할수 있다.

  $abc'd' + abcd' = abd'$
  $[X = abd', Y = c]$

  $(a + bc)(d + e') + a'(b'+ c')(d + e') = d + e'$
  $[X = d + e′,Y = a + bc,Y′ = a′(b′ + c′)]$

• $X + XY = X$를 이용하여 항을 제거한다.

  $a'b + a'bc = a'b$
  $[X = a'b]$

• X + X′Y = X + Y를 이용하여 항을 제거한다.
  

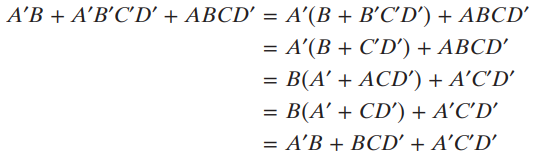
• 쓸모없는 항을 이용해 줄인다

---

3.5 Proving Validity of an Equation

1. 양쪽 Equation의 Truth table을 만들어 비교한다.
2. 여러가지 법칙을 적용해 한쪽이 다른쪽과 같아질때까지 바꿔나간다.
3. 양쪽에 여러가지 법칙을 적용해 서로 같아지게 한다.
4. 양쪽에 완전히 똑같은 법칙을 적용하는것은 불가능하다.

증명 방법

1. 양쪽 사이드를 곱의 합(Sum of product) 형식으로 줄인다.
2. 양쪽을 비교해 다른지 확인한다.
3. 다른쪽에 존재하는 항을 반대편에도 추가해본다.
4. 다른쪽에 없는 항을 제거해본다.