[Day 50] SVM

임종우·2022년 11월 22일

SVM

ai_school_TIL

목록 보기

32/34

11.22. 오후
KMOOC 강의 중 SVM 부분을 수강하고 공부하였다.

SVM

최적의 결정 경계(Decision Boundary), 즉 데이터를 분류하는 기준 선을 정의하는 모델
관측치들을 가장 잘 구분해주는 hyperplane 혹은 vector, 분류함수를 찾아내는 것
결정 경계와 Support Vector 사이의 거리 margin이 최대화되는 결정경계를 찾는 기법
Support Vector란, 결정경계와 가장 가까이 있는 데이터 포인트들을 의미한다.
SVM은 수리적 최적화 모형으로 모델링되며 해당 문제를 해결해서 최종 모델을 결정한다.

특징

선형이나 비선형 분류, 회귀, 이상치 탐색에도 사용할 수 있는 머신러닝 방법론이다.
딥러닝 이전 시대까지 널리 사용되었다.
고차원의 복잡한 분류 문제를 잘 해결할 수 있다.
상대적으로 작거나 중간 크기를 가진 데이터에 적합하다.
딥러닝보다 앙상블, SVM등이 더 좋은 성능을 보이는 분야들도 존재한다.
margin 을 최대화하면 이상치에 강건(robust)해지는 효과가 존재한다.
SVM은 스케일에 민감하기 때문에 변수들 간의 스케일을 잘 맞춰주는 것이 중요
(스케일링이 안된 상태에선 스케일이 큰 특정 변수의 변동성에 굉장히 민감할 수 있음)
Sklearn의 standard scaler를 사용하면 스케일을 잘 맞출 수 있다 꼭 필요!

margin

margin은 support vector와 decision boundary 사이의 길이였다.

SVM에서는 Hard margin 과 Soft margin을 사용할 수 있다.

Hard margin
두 클래스가 하나의 선으로 완벽하게 나누어진다.
결정경계를 넘어서서 존재할 수 없다.
Soft margin
일부 데이터들이 분류 경계선의 분류 결과에 반하는 것을 일정 수준 허용한다.
몇몇 데이터가 결정 경계를 넘어서서 존재할 수 있다.
C 페널티 파라미터를 통해 얼마나 허용해줄지를 조정할 수 있다.
C가 작으면 페널티가 작으니까 더 많이 넘어갈 수 있고, margin이 커진다.
Margin은 더 넓지만 train set 의 오차는 더 커지는 trade-off가 발생한다.

수식

출처 위키백과에 잘 정리되어 있다. 그래도 이해하기 위해 따라써보자!

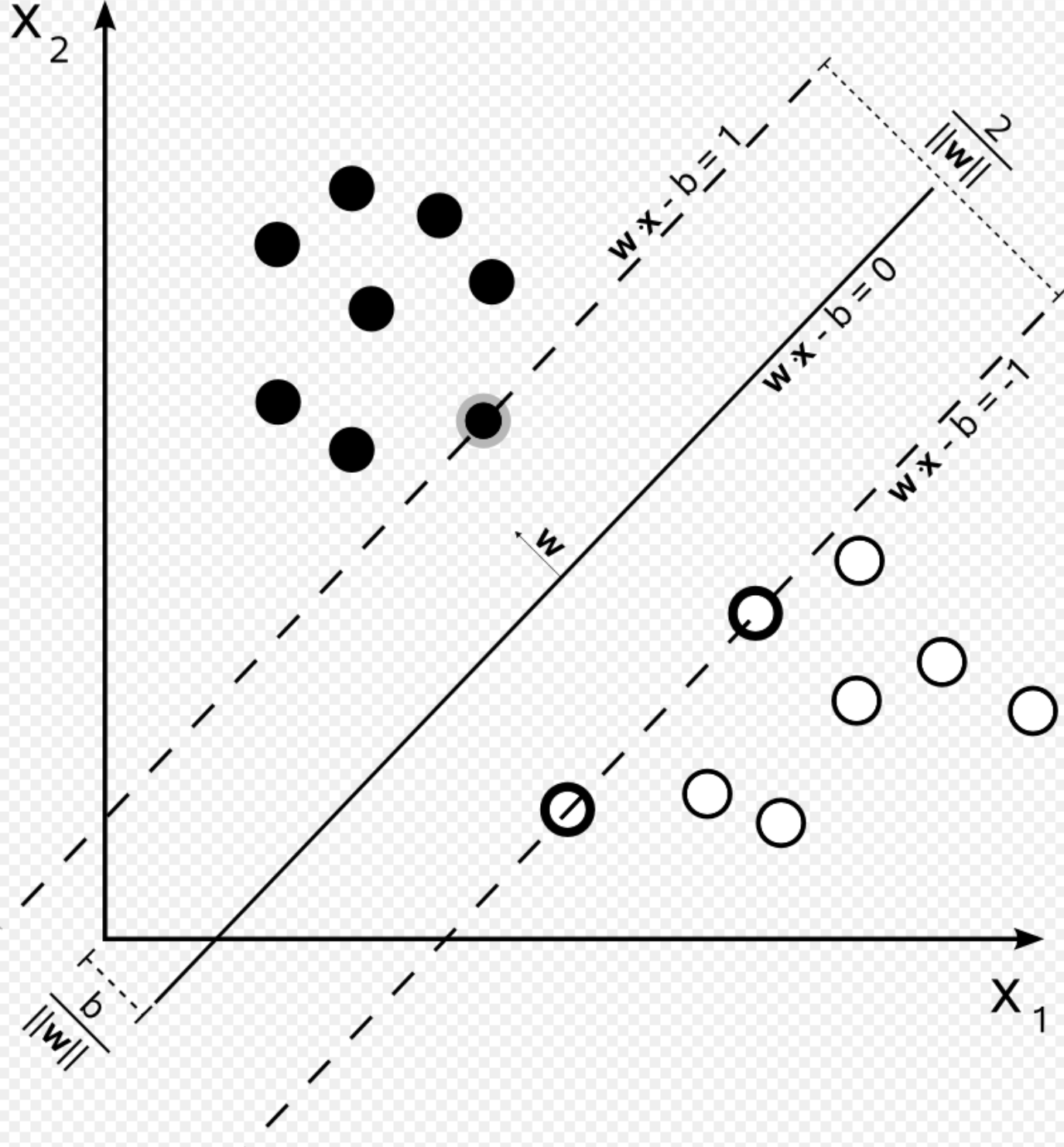
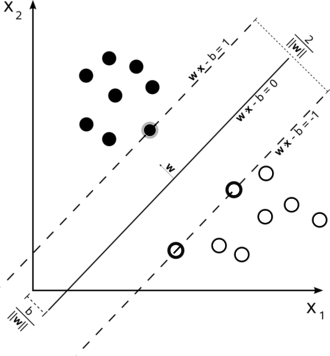
위와 같은 데이터 집합에 대해서, yi는 데이터가 어느 집합에 포함되는지를 나타내는 값으로 1과 -1이다.
사진과 같이 나누어지는 데이터와 결정경계, margin이 존재할 때,
결정경계는 다음과 같이 나타낼 수 있다.

또한, 서포트 벡터가 존재하는 벡터 역시 역시 우변이 +1, -1인 식으로 표현할 수 있다.
그렇다면, 두 벡터(hyperplane) 사이의 거리를 수식으로 구해보았을때, 이는 마진을 의미하는 값이며,
이다.

그렇다면, 결정경계와 마진 사이엔 데이터가 존재하지 않아야 하므로, 이를 조건식으로 나타낼 수 있고, 결국 마진을 최대화 해야하는 서포트 벡터 머신 문제는 아래와 같은 수식을 통해 표현할 수 있다고 한다.

하지만 이때, ||w||가 루트를 포함하고 있으므로 풀기 어렵다. 따라서 이를 제곱으로 치환해도 해는 변하지 않으므로 다음과 같이 문제가 정의된다고 한다.

soft margin의 경우, 결정경계를 넘어가서 존재하는 데이터 샘플들의 결정경계까지의 거리를 프사이라고 하였을때, 다음과 같은 식을 통해 문제가 정의된다.

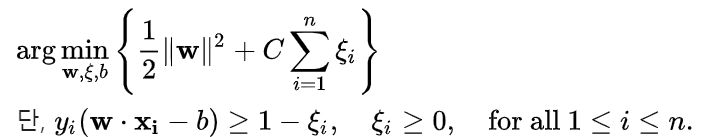
nonlinear SVM

일반적인 SVM의 경우, 선형적으로 평면을 그려주어 데이터들을 분류한다.
그러나, 선형적으로 분류할 수 없는 데이터들이 존재하는 비선형 문제에 대해서도 SVM을 사용할 수 있다. 비선형적인 평면을 그려줄 수 있다는 뜻이다!
바로 kernel을 이용하면 된다.

커널이란, 데이터의 차원을 높여줄 수 있는 변환 함수이다.
여기를 참고해야겠다!

예를 들어 한 가운데 원의 형태를 이루며 존재하는 데이터 클래스 A들과 그 밖에 존재하는 클래스 B 데이터들이 있다면, z = x^2 + y^2라는 식을 세운 후 xz평면에 데이터들을 표시한다. 그렇다면 해당 차원에서는 데이터들이 선형 평면을 통해 나눠지게 된다.
-> 고차원에서 linear 한 구분선이 저차원에서는 non-linear하게 표시된다는 것이다!

따라서 저차원 공간을 고차원 공간으로 변환해주어 선형 구분선을 그린다면 저차원공간에 비선형적인 구분선을 그려 SVM을 사용할 수 있다.

kernel에는 다양한 종류의 함수가 존재한다고 한다. 이건 차차.. 필요하면 알게 되겠ㅈ!
강의에서는 polynomial kernel과 Gaussian RBF(Radial Basis Function) kernel이라는 것이 존재한다 까지 다루셨다. Gaussian을 많이 사용한다고 한다!

scikit-learn에서는 kernel 이라는 하이퍼파라미터를 통해 설정할 수 있고, gamma라는 하이퍼파라미터를 통해 고차항 차수에 대한 정도, 즉 복잡도를 조절할 수 있다. C를 통해 앞에서 알아본 C 페널티도 조절할 수 있다.

SVM Regression

SVM을 통해 회귀 역시 진행할 수 있다.

분류와 마찬가지로 회귀 식(결정경계의 역할)에 대해 이와 평행한 오차 경계선을 두고, 회귀식과 관측치 사이 어느 정도의 오차까지는 허용하되, 오차가 그 이상으로 넘어가는 것은 허용하지 않는 방식으로 SVM을 사용해 회귀식을 예측한다.
오차 한계선과 회귀식 사이의 너비가 최대가 되도록 하고, 그 한계선을 넘어가는 관측치들에 대해서는 입실론을 통해 패널티를 부여한다.

비선형적인 회귀 선을 가지는 데이터들에 대해서도 유연하게 SVM을 이용해 회귀 예측을 진행할 수 있다. kernel을 이요한 비선형적 SVM을 사용한다. 입력변수들이 고차원의 공간에서 선형적인 회귀식을 구성하고, 이것들이 본 차원의 공간에서는 비선형적으로 구성되는 것과 같은 효과를 내는 테크닉을 이용한다!

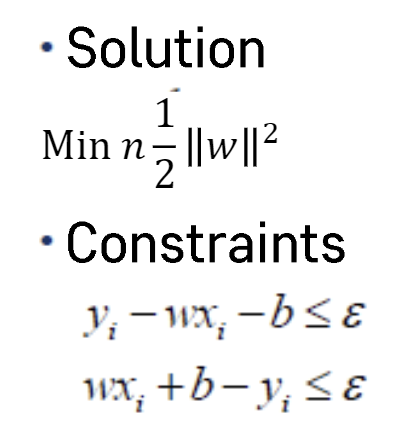
위와 같이 수식으로 나타낼 수 있다.

soft margin을 사용할 경우에는 프사이를 추가로 도입하여 사용하면 되겠다.

scikit-learn 에서

from sklearn.svm import SVC

clf = make_pipeline(StandardScaler(), SVC(gamma='auto'))
clf.fit(X, y)

print(clf.predict([[-0.8, -1]]))

공식문서

C, kernel, degree, gamma 등의 하이퍼파라미터를 조정할 수 있다.

from sklearn.svm import LinearSVR, SVR

regr = make_pipeline(StandardScaler(), SVR(C=1.0, epsilon=0.2))
regr.fit(X, y)

# 또는
regr = make_pipeline(StandardScaler(),
                     LinearSVR(random_state=0, tol=1e-5))
regr.fit(X, y)