👨‍🏫 본 글은 칸 아카데미의 수업을 듣고 정리한 글 입니다.

• Transpose of a matrix
• Determinant of transpose
• Transpose of a matrix product
• Transpos of sums and inverse
• Transpos of a vector
• Rowspace and left nullspace
• Visualizations of left nullspace and rowspace

---

Transpose of a matrix

🎈 이번 강의에서는 Transpose matrix(전치행렬)에 대해 학습합니다.

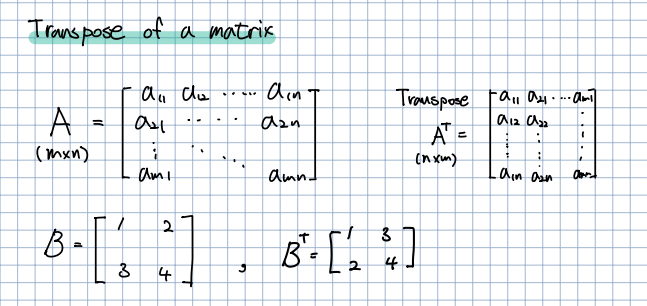
🎈 임의의 행렬 $A$($m \times n$)이 존재할 때 $A$를 Transpose하면 $A^T$라고 표기하며 ($n \times m$) 크기의 행렬로 바뀌게됩니다. 위의 예시를 보면 대각행렬을 기준으로 서로 바뀌는 것을 알 수 있습니다.

Determinant of transpose

🎈 이번 강의에서는 transpose의 행렬식에 대해 학습합니다.

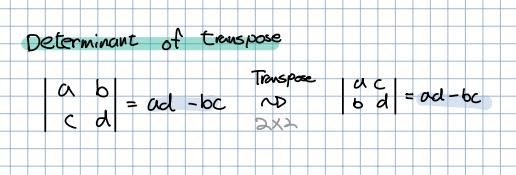
🎈 먼저 $2 \times 2$ 크기의 행렬에서는 위와 같이 동일한 det(행렬식)을 가지는 것을 확인할 수 있습니다.

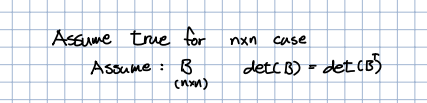
🎈 위와 같이 $n \times n$의 행렬식이 전치행렬가 같다고 가정하면, $n+1 \times n+1$의 행렬 또한 행렬식이 같은지 확인해보겠습니다.

🎈 먼저 n+1=m 이라고 생각하고, 임의의 행렬 $A$($m \times m$)에 대한 행렬식을 구해보겠습니다.
$det(A)$에 대해 구해보면 위와 같은 식이 나옵니다. $A^T$($m \times m$)에 대한 행렬식을 구하면 det안의 부분행렬이 전치되는 것을 확인할 수 있습니다.

🎈 $A$과 $A^T$의 det의 차이는 부분행렬이 전치되었다는 것인데, 각각의 부분행렬은 $n \times n$ 행렬임을 알 수 있습니다. 앞서 $n \times n$ 행렬$A$와 전치된 행렬$A^T$의 행렬식이 같다는 것을 가정했기 때문에, 결과적으로 $n+1 \times n+1$의 행렬 또한 행렬식 또한 같다는 것을 확인할 수 있습니다.

Transpose of a matrix product

🎈 오늘은 행렬의 Transpose(전치)에 대해 학습합니다.

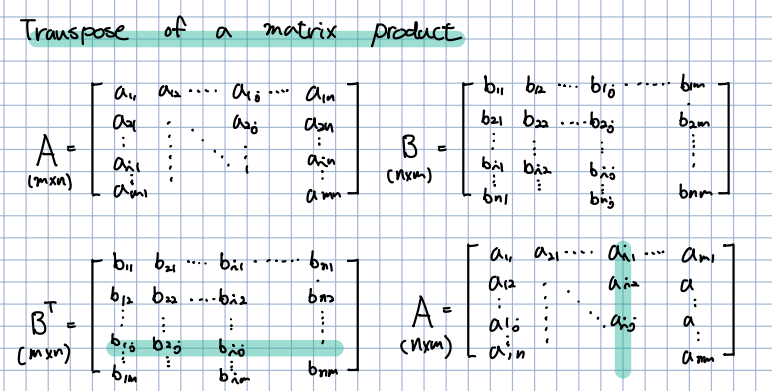
🎈 먼저 행렬 $A, B$가 존재하며 각각 $m \times n$ $n \times m$ 크기를 가지는 행렬이며, 이들의 전치행렬은 반대의 크기를 가질겁니다.

🎈 행렬 $C$를 $A \cdot B$라고 하며, $D$는 $A^T \cdot B^T$라고 할 때(위 필기의 -1표시는 오기입니다) 각각의 행렬 $C,D$의 $i,j$ 지점의 값을 위의 식처럼 구할 수 있습니다. 위 식에서 하나 확인할 수 있는 것은 $C_{i,j}$ = $D_{i,j}$ 라는 것이며, 이는 다시 이야기하면 $C^T$ = D와 같다고 이야기할 수 있습니다.

🎈 결과적으로 임의의 행렬 $(AB)^T$=$B^TA^T$ 라고 말할 수 있습니다.

Transpose of sums and inverse

🎈 이번 강의에서는 전치행렬의 합과 역에 대해 학습합니다.

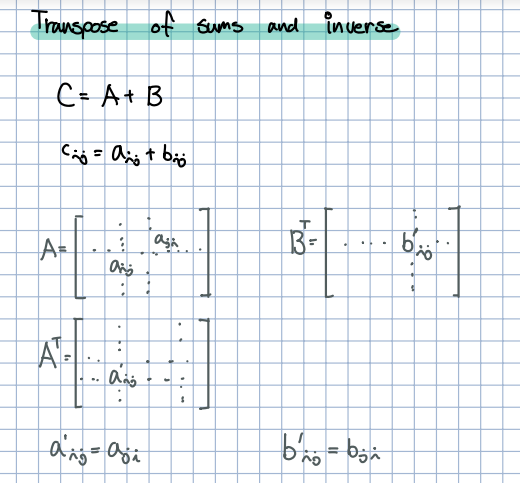
🎈 행렬 $C$= $A + B$라고하면, $c_{ij}$ = $a_{ij}$ + $b_{ij}$ 라고 말할 수 있습니다. $A^T$의 $a^\prime_{ij}$ = $a_{ji}$, $B^T$의 $b^\prime_{ij}$ = $b_{ji}$라고 말할 수 있습니다.

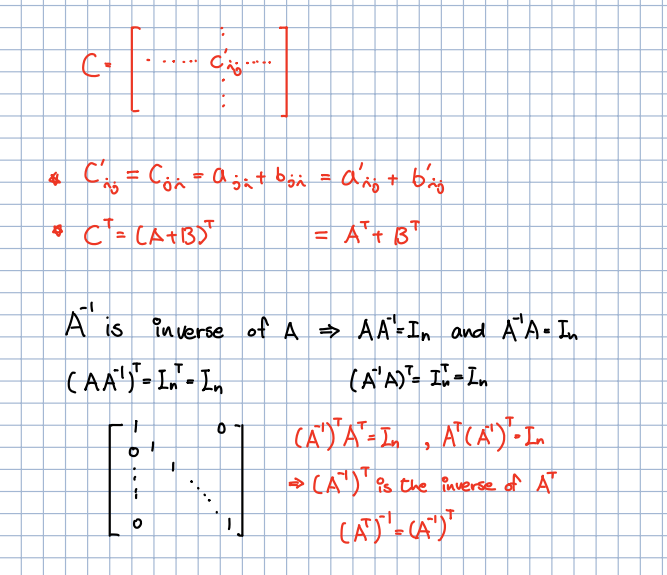
🎈 그렇다면 $C^\prime_{ij}$ = $C_{ji}$ = $a_{ji} + b_{ji}$ = $a^\prime_{ji} + b^\prime_{ji}$ 라고 말할 수 있습니다. 결과적으로 $C^T = (A+B)^T$ = $A^T + B^T$ 라고 말할 수 있습니다.

🎈 행렬 $A^{-1}$와 Transpose와의 관계는 위의 식을 따라가다보면 어렵지 않게 이해하실 수 있습니다. 결과적으로 $(A^{-1})^T$ = $(A^{T})^-1$ 입니다.

Transpose of a vector

🎈 오늘은 벡터의 전치에 대해 학습합니다.

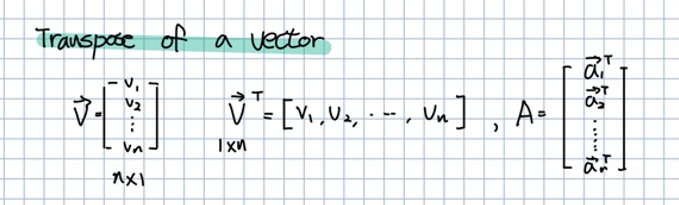
🎈 n x 1 벡터인 $\vec{v}$을 전치하면 1 x n 벡터인 $\vec{v}^T$ 벡터가 됩니다.

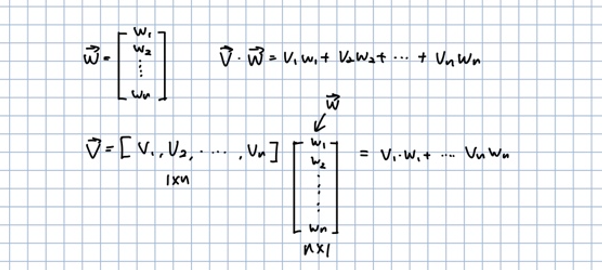
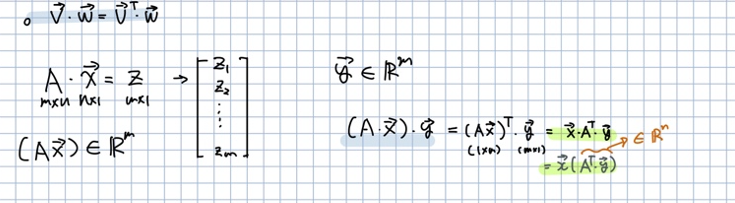
Rowspace and left nullspace

🎈 이번 강의에서는 Rowspace(행공간)과 left nullspace에 대해 학습합니다.

🎈 임의의 행렬 $A$에 대한 영공간을 계산합니다. 이전에 rref(기약행사다리꼴)을 통해 영공간을 계산할 수 있다는 것을 배웠습니다. rref(기약행사다리꼴)을 계산을 하면 pivot table과 free value를 통해 영공간을 찾을 수 있습니다.

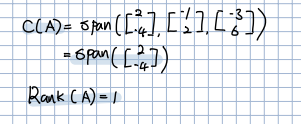
🎈 열공간 $C(A)$의 경우 역시 rref(기약행사다리꼴)을 통해 pivot table을 사용해 쉽게 계산할 수 있습니다. Rank 또한 rref을 통해 구할 수 있습니다.

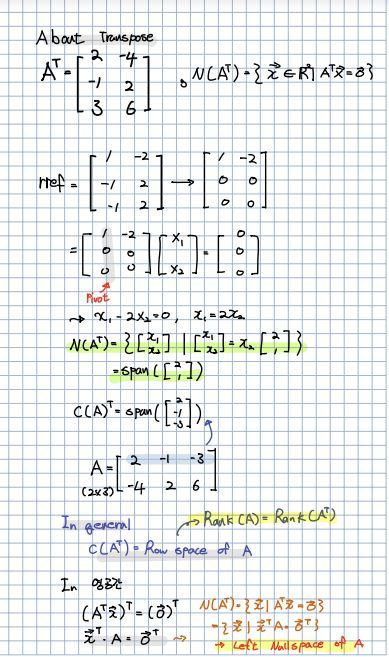
🎈 위의 과정은 지금까지 배웠던 열공간과 영공간에 대해 계산했습니다. 이번에는 임의의 행렬 $A^T$에 대한 행공간과 left nullspace에 대해 계산합니다. 계산하는 방법은 위의 방법와 동일합니다. rref(기약행사다리꼴)을 통해 계산할 수 있습니다. 다른 점이라고 하면 행렬 $A$ 기준으로 봤을 때 pivot값과 free value값이 기존의 열공간이 아닌 행공간과 기존의 영공간과 다른 점을 확인할 수 있습니다.

🎈 결과적으로 행공간은 임의의 전치행렬의 열공간이라고 말할 수 있으며, 항상 같은 rank를 가지며, 영공간의 경우에는 같지는 않으면 left nullspace라고 부릅니다.

Visualizations of left nullspace and rowspace

🎈 이번 강의에서는 이전 학습 했던 행공간, 열공간 등등에 대한 관계에 대해 학습합니다.

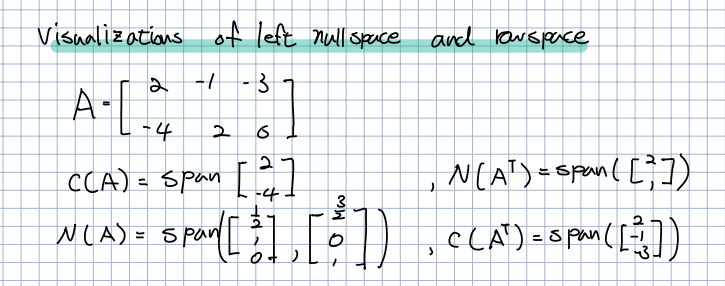
🎈 앞서 배웠던 값들을 그대로 사용합니다.

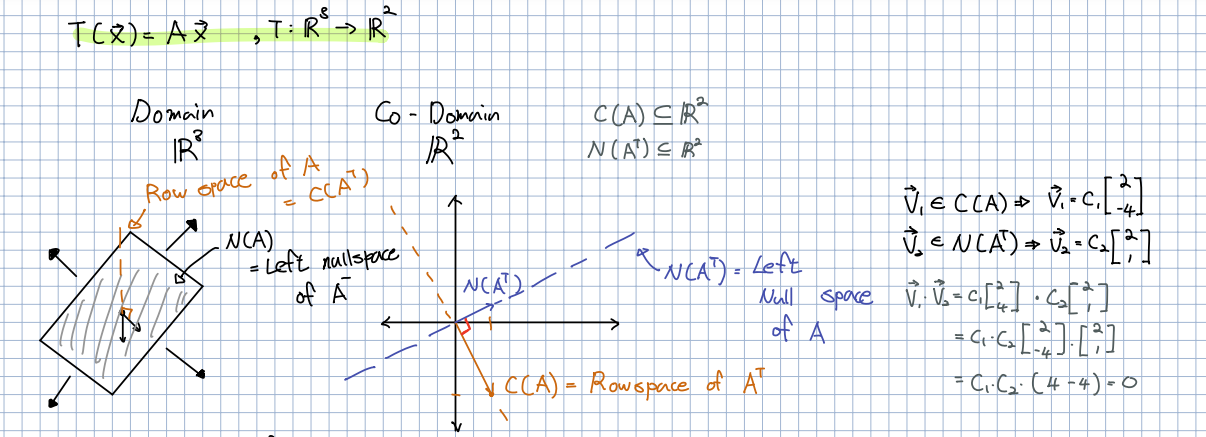
🎈 위의 Co-Domain 영역에서의 $C(A)$와 $N(A^T)$ 시각화 하면 위와 같이 표현할 수 있습니다. 위의 그래프에서 확인할 수 있듯이, $C(A)$와 $N(A^T)$이 직교하는 것을 알 수 있습니다. 이는 수식적으로도 내적을 통해 확인 할 수 있습니다.

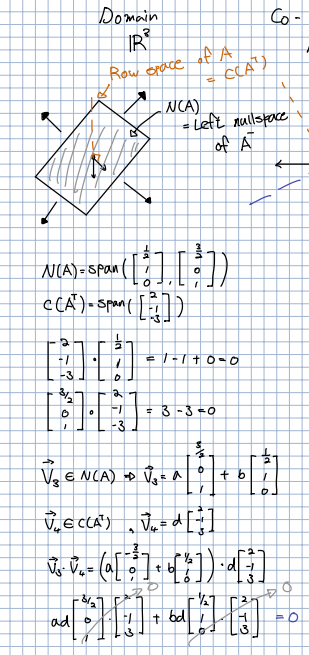
🎈 $R^3$ 공간인 Domain 영역에서의 $N(A)$과 $C(A^T)$ 시각화 하면 위와 같이 표현할 수 있으며, 이 역시 서로 직교하면 내적이 0인것을 확인할 수 있습니다.

🎈 이에 대한 증명 과정은 다음 강의에서 학습한다고 이야기합니다.