👨‍🏫 본 글은 칸 아카데미의 수업을 듣고 정리한 글 입니다.

• Visualizing a column space as a plane in $R_3$
• Proof: Any subspace basis has some number of elements
• Dimension of the null space or nullity
• Dimension of the column space or rank]
• Showing relataion between basis cols and pivot cols
• Showing that the candidate basis does span C(A)

---

Visualizing a column space as a plane in $R_3$

🎈 오늘은 Null space and column space 1에서 이어지는 내용들입니다. 이번 강의에서는 두 열벡터가 이루는 평면에 대해 학습하며, 그 평면을 구하는 방법들에 대해 학습합니다.

🎈 위의 basis인 $C(A)$는 앞서 구한 열공간의 기저 입니다. 먼저 두 열벡터를 위와 같이 3차원 공간의 그래프로 표현할 수 있는데, 앞서 배운 법선벡터와 평면 위의 벡터의 관계를 통해 법선 벡터와 평면을 구할 수 있습니다.

🎈 평면 위의 $\vec{x}$의 값을 사용해 $5x - y - z = 0$라는 평면을 구할 수 있습니다. 위의 방법은 외적과 법선벡터를 사용해 구한 방법입니다.

🎈 다른 방법은 기존의 행렬 $A$의 rref(기약행사다리꼴)을 구해 찾는 방법입니다. 행렬 $A$와 $\vec{b}$를 사용해 위와같은 rref를 구할 수 있었습니다. 마지막 행을 보면 $5x-y-z = 0$이어야만 해를 찾을 수 있습니다.

Proof: Any subspace basis has some number of elements

🎈 이번 강의에서는 Any subspace basis has some number of elements대해 학습합니다. 즉, 부분공간 기저의 요소들의 수는 항상 같아야 한다 이야기 할 수 있을 것 같습니다.

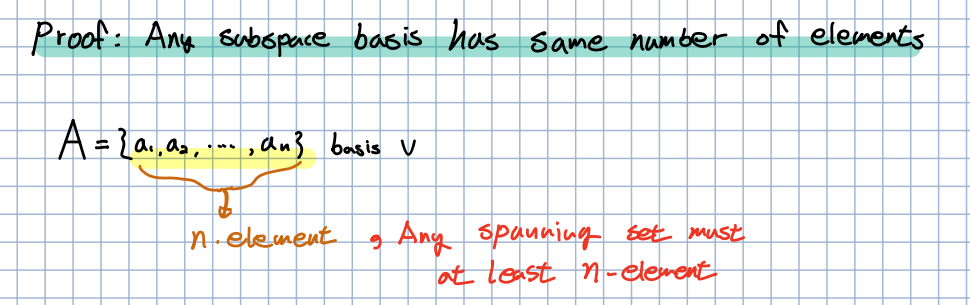
🎈 V의 기저인 집합 $A$가 n개의 elements를 가진다면, 어떤 spanning set이든 적어도 n개의 요소를 가져야 합니다.

🎈 이에 대한 증명을 잘못된 예시를 통해 진행합니다. 집합 $B$을 통해 증명을 하는데, 이 과정이 궁금하다면 강의를 들으시는 것을 추천드립니다. 결과적으로 이 과정은 왜 적어도 n개의 요소를 가져야하는 증명합니다.

🎈 위의 과정을 통해 집합 $B$를 집합 $A$의 일부만 사용해 표현할 수 있습니다. 앞에서
집합 $B$를 V의 spans라고 표현하는데, 집합 $B$를 집합 $A$의 일부만 사용해 표현할 수 있다면 이는 성립하지 않습니다. 결론적으로 위의 가정이 성립할려면 적어도 n개의 요소 이상이여야만 한다는 것을 알 수 있습니다.

🎈 결론적으로 V의 차원의 수는 basis의 요소들의 수로 결정됩니다.

Dimension of the null space or nullity

🎈 이번 시간에는 영공간의 차원에 대해 학습합니다.

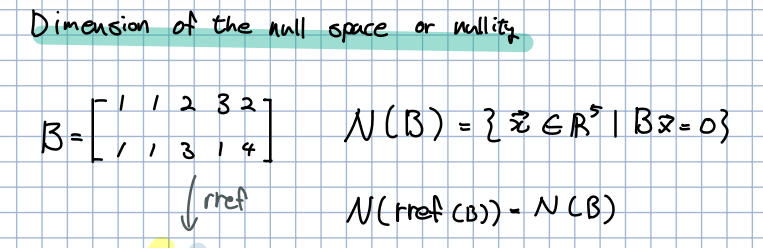
🎈 영공간에 대한 정의는 위와 같이 표현할 수 있습니다. 이는 지금까지 배웠던 것이므로 설명은 생략하겠습니다.

🎈 행렬 $B$의 영공간을 찾기 위해 먼저 rref(기약행사다리꼴)을 구합니다. rref 구하는 것 역시 설명은 생략하겠습니다. rref를 사용해 $\vec{x}$를 각각의 free value들로 표현할 수 있습니다. 각각의 free value들로 표현한 벡터들($\vec{v_1}, \vec{v_2}, \vec{v_3})$은 행렬 $B$의 영공간이면서 span이라고 말할 수 있습니다. 또한 각각의 선형 독립이기에 영공간의 basis라고 말할 수 있습니다.

🎈 또한 앞서 부분공간의 차원에 대해 학습했었습니다. 방금 우리가 정의 $N(B)$의 차원은 3이라고 말할 수 있습니다. 이는 또 nullity(행렬)이라고도 부르는데, 결과적으로 nullity(행렬)은 rref(행렬)의 자유변수의 수라고 말할 수 있습니다.

Dimension of the column space or rank

🎈 이번시간에는 열공간의 차원에 대해 학습합니다.

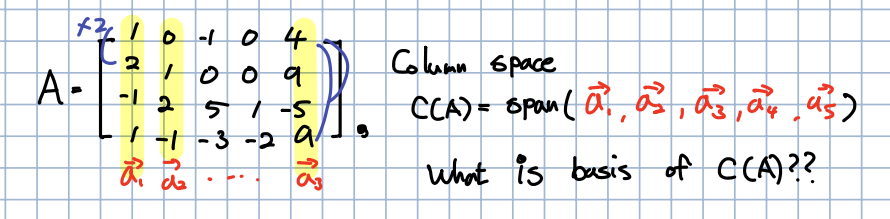
🎈 행렬 $A$가 위와 같이 존재하며, $C(A)$ 즉, 열공간이 $(\vec{a_1}, \vec{a_2}, \vec{a_3}, \vec{a_4}, \vec{a_5})$ 라고 정의합니다. 그렇다면 $C(A)$의 기저는 무엇일까요? 기저의 정의, span이어야 하며, 선형 독립이어야 합니다.

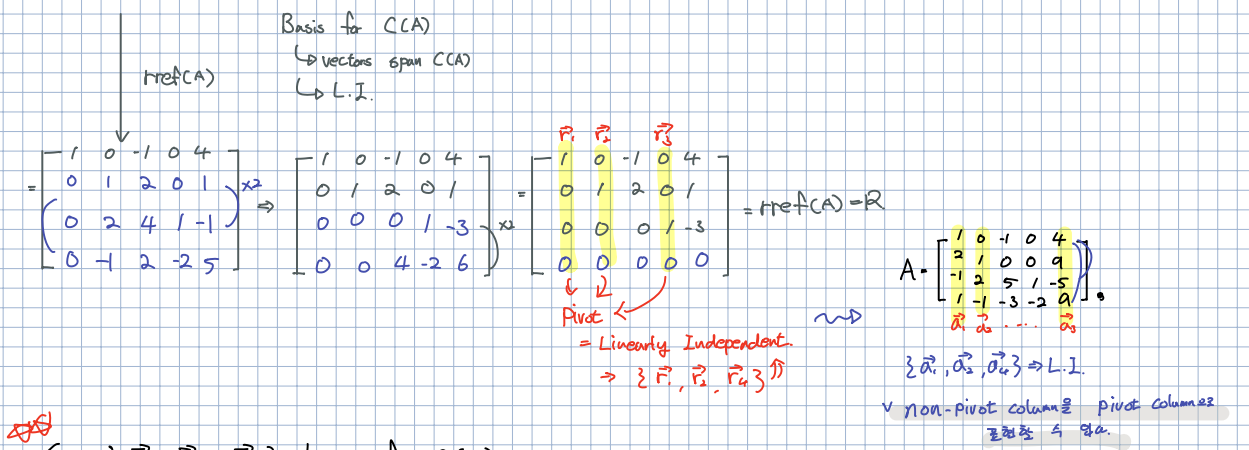
🎈 행렬 $A$의 rref를 구합니다. rref를 구해 각각의 pivot, free value들을 찾을 수 있습니다. 각각의 pivot value들은 선형 독립함을 알 수 있으며, 이는 행렬 $A$의 $\vec{a_1}, \vec{a_2}, \vec{a_4}$ 열벡터들이 선형 독립함을 의미한다고 합니다. 또한 나머지 열벡터들을 $\vec{a_1}, \vec{a_2}, \vec{a_4}$로 표현 할 수 있다고 합니다.

🎈 결과적으로 {$\vec{a_1}, \vec{a_2}, \vec{a_4}$}는 $C(A)$의 기저라고 말할 수 있으며, $C(A)$의 차원은 3이며 이는 rank(A)라고도 부릅니다.

Showing relataion between basis cols and pivot cols

🎈 이번 시간에는 rref의 pivot 값들의 관계가 기존 행렬의 열벡터들의 관계에서도 성립하는지 학습합니다.

🎈 기존에 사용했던 행렬 $A$와 $rref(A) = R$을 그래도 사용합니다. 행렬 $R$의 pivot 벡터들이 각각 선형 독립하는 것을 알고 있습니다. 이는 어떤 rref 행렬이든 pivot 벡터들끼리는 선형 독립임을 알 수 있습니다. 또한 선형 독립이라는 의미는 $C_1\vec{r_1} + C_2\vec{r_2} + C_4\vec{r_4} = 0$ 에서 오직 $C_1, C_2, C_4 = 0$일때만 식이 성립한다는 것을 의미합니다.

🎈 rref의 특징 중 하나는 영공간이 같다는 것입니다. 즉 $R$, $A$의 영공간이 같다는 것을 의미합니다. 영공간 또한 rref로 해를 찾기 때문에, 이는 $R$, $A$가 동일한 해를 가진 다는 의미이며, $A$의 ${\vec{a_1}, \vec{a_2}, \vec{a_4}}$ 선형 독립임을 알 수 있습니다.

Showing that the candidate basis does span C(A)

🎈 이어서 ${\vec{a_3},\vec{a_5}}$의 열벡터들을 ${\vec{a_1}, \vec{a_2}, \vec{a_4}}$의 열벡터들의 선형결합으로 만들 수 있는지 학습합니다.

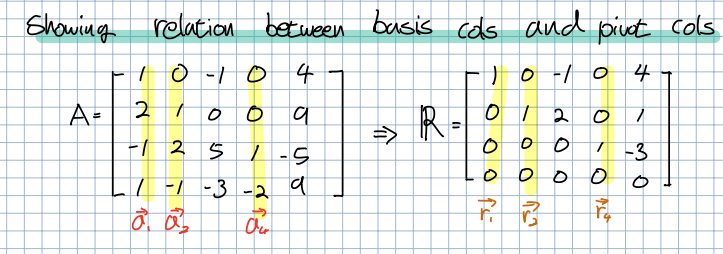
🎈 이번 강의 역시 기존에 사용한 행렬들을 사용합니다.

🎈 위의 그림에서 $\vec{A} \cdot \vec{x} = 0, \vec{B} \cdot \vec{x} = 0$를 $x_1\vec{a_1} + x_2\vec{a_2} + x_3\vec{a_3} + x_4\vec{a_4} + x_5\vec{a_5} = 0$, $x_1\vec{r_1} + x_2\vec{r_2} + x_3\vec{r_3} + x_4\vec{r_4} + x_5\vec{r_5} = 0$ 로 각각 표현할 수 있습니다. 또한 각각의 pivot과 free 값들을 알 수 있습니다. Free value는 말 그래도 어떤 실수 값이든 집어 넣을 수 있습니다. 그렇기에 $x_3 = -1, x_5 = 0$으로 넣고 $\vec{a_3}$에 대한 식을 정의 할 수 있는데, 이는 곧 ${\vec{a_1}, \vec{a_2}, \vec{a_4}}$ 벡터들의 선형결합임을 알 수 있습니다.

🎈 결론적으로 ${\vec{a_3},\vec{a_5}}$의 열벡터들을 ${\vec{a_1}, \vec{a_2}, \vec{a_4}}$의 열벡터들의 선형결합으로 만들 수 있으며, 이 말은 즉 ${\vec{a_3},\vec{a_5}}$ span에서 필요없는 벡터 입니다.