👨‍🏫 본 글은 칸 아카데미의 수업을 듣고 정리한 글 입니다.

• Linear combinations and span

Linear combinations and span

🎈 선형 결합이란 위에서 볼 수 있듯이, 상수배를 한 벡터들의 합으로 나타낼 수 있습니다. 수업에서 위의 회색 박스가 전부라고 이야기 합니다. (실제로 그런거 같습니다..ㅎ)

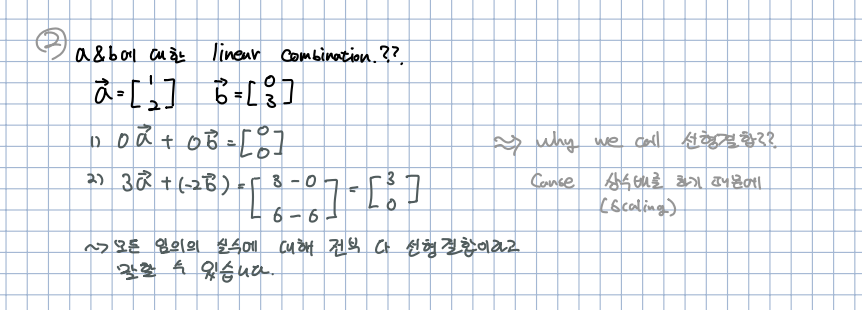
🎈 $\vec{a} = \begin{bmatrix} 1 \\ 2 \end{bmatrix}$, $\vec{b} = \begin{bmatrix} 0 \\ 3 \end{bmatrix}$ 에 대한 선형결합을 위에서 제시합니다. 위에서 볼 수 있듯이 단순히 각각의 벡터의 상수배를 한 값들의 합을 나타냅니다. 여기서 상수배는 실수 전체 범위를 의미합니다.

🎈 그렇다면 왜 선형 결합이라고 호칭할까요? 이유는 바로 상수배를 곱하기 때문입니다. 벡터끼리 곱하거나 하지 않습니다. 오직 상수배를 곱한 값들의 합을 의미합니다.

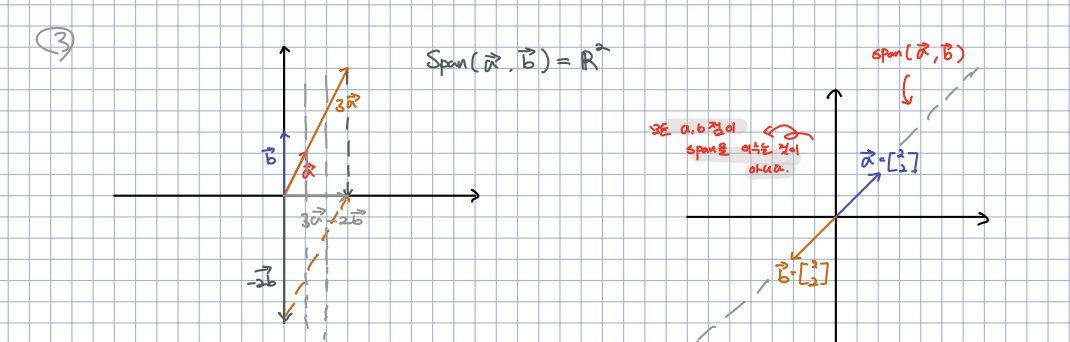
🎈 조금 더 시각적으로 확인해보겠습니다. 첫번째 그래프에서 즉, 위에서 언급한 $\vec{a}$, $\vec{b}$의 벡터들로는 $\mathbb{R}^2$의 모든 값들을 표현할 수 있습니다. 이를 $span(\vec{a}, \vec{b})$라고 표현하며, $span(\vec{a}, \vec{b}) = \mathbb{R}^2$ 라고 표현할 수 있습니다.

🎈 반대로 $\vec{a} = \begin{bmatrix} 2 \\ 2 \end{bmatrix}$, $\vec{b} = \begin{bmatrix} -2 \\ -2 \end{bmatrix}$를 보여주는 두번째 그래프의 span은 무었일까요? 이 두선으로 표현할 수 있는 부분은 직선뿐이 보이지 않습니다. 결국 span은 하나의 직선이라고만 말할 수 있습니다.

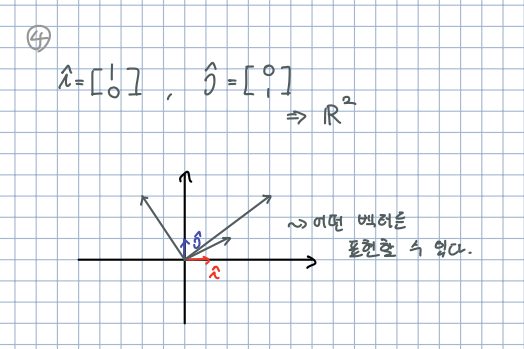
🎈 전에 학습했던 Unit Vector의 span 또한 $\mathbb{R}^2$이라고 표현할 수 있습니다. 조금 생각 해보면 당연하다고 생각할 수 있습니다.

🎈 span에 대해 정의한다면 특정 벡터들이 표현할 수 있는 공간이라고 설명할 수 있을것 같습니다.

👨‍🏫 Linear combination과 span에 대해 학습했습니다. 단순히 식을 보면 간단해 보이지만, 이해하는데는 쉽지 않다고 생각합니다.