[Shorts 선형대수학] Vectors-2

👨‍🏫 본 글은 칸 아카데미의 수업을 듣고 정리한 글 입니다.

• Vector examples
• Unit vectors intro
• Parametric representations of lines

Unit Vector

🎈 Unit Vector는 단위 벡터라고 부릅니다. 쉽게 길이가 1인 벡터들이라고 정의할 수 있습니다. 또한 단위 벡터는 각 차원의 수 만큼 존재합니다.

🎈 $\mathbb{R}^2$, 2 차원 실수공간에서는 $\vec{i} = \begin{bmatrix} 1 \\ o \end{bmatrix}$ , $\vec{j} = \begin{bmatrix} 0 \\ 1 \end{bmatrix}$ 가 존재합니다. 단위 벡터의 특징은 각 단위 벡터들의 연산으로 모든 2차원의 벡터를 표현 할 수 있습니다.

Parametric representations of lines

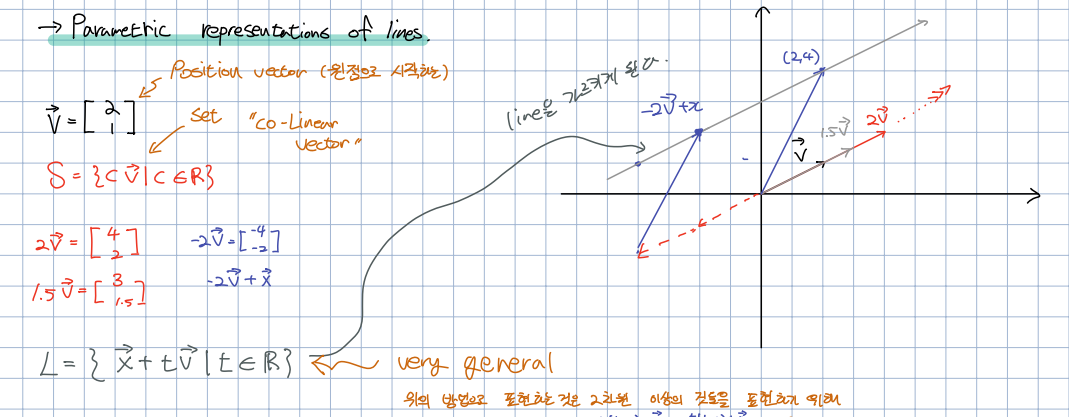
🎈 Parametric representations of lines를 간단하게 설명하면 그 동안 일반적으로 표현했던 $y=ax+b$와 같은 직선의 방정식을 벡터로 표현하는 것입니다. "왜 어렵게 벡터로 표현하냐"라고 하면, 위와 같은 방법으로는 3차원에서의 직선의 방정식은 표현할 수 없습니다.

🎈 $\vec{V} = \begin{bmatrix} 1 \\ o \end{bmatrix}$ 를 원점에서 시작하는 Position vector라고 한고, 위의 집합 S는 $C \vec{V}$ 라고 표현하며, $C$는 실수 전체의 집합입니다. $\vec{V}$벡터에 어떤 스칼라를 곱해도 방향은 달라지지 않습니다.

🎈 $\vec{X} = \begin{bmatrix} 2 \\ 4 \end{bmatrix}$ 일 때 $\vec{X} + -2\vec{V} = \begin{bmatrix} -2 \\ 2 \end{bmatrix}$ 의 좌표를 가르킵니다. 저희는 벡터를 사용해 이 두 지점에 지나는 직선의 방정식을 표현할 수 있습니다. 위의 집합 $L$이 바로 두 지점을 지나는 직선의 방정식 입니다.

🎈 다른 예시로 위의 $\vec{b} - \vec{a}$의 방향을 지나는 직선의 방정식을 세울려고 합니다. 위와 같은 방법으로 집합 $L$의 식을 세울 수 있습니다. 각각의 첫번째 행의 값을 x, 두번째 행의 값을 y로 생각하면 $x= -2t$, $y= 2t + 3$과 같은 직선의 방정식을 세울 수 있습니다.

🎈 또한 3차원에서의 직선의 방정식을 벡터를 사용해 위와 같이 계산할 수 있습니다.

👨‍🏫 단위 벡터와, Parametric representations of lines에 대해 학습했습니다.