👨‍🏫 본 글은 칸 아카데미의 수업을 듣고 정리한 글 입니다.

• Solving a system of 3 equations and 4 variables using matrix row-echelon form
• Solving linear systems with matrices
• Using matrix row-echelon form in order to show a linear system has no solutions

Solving a system of 3 equations and 4 variables using matrix row-echelon form

🎈 오늘은 Reduce Row echelon form에 대해 학습합니다.

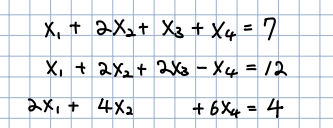
🎈 위에는 미지수가 4개인 3개의 방정식이 존재합니다. 미지수가 방정식보다 많으면 무한한 해를 가질 수 있습니다. 위의 식이 4차원 공간이면 평면으로 제한될 수 있습니다. 만약 3차원이면 선으로 제한할 수 있습니다. 위의 방정식의 해를 찾기 위해 Reduce Row echelon form(rref)의 형태로 만들어 해를 찾을 수 있습니다.

🎈 각각의 연립방정식을 행렬 $A$의 형태로 만들 수 있습니다. 각각의 행의 연산을 통해 결과적으로 rref(A)의 형태를 만들 수 있습니다. 위 형태에서 $1$은 pivot entry라고 부르며, 나머지는 free variables 라고 부릅니다.

✔ Reduce Row echelon form의 조건으로는 위의 형태를 만족해야합니다.

🎈 결과적으로 rref(A)를 사용해 위와 같은 식을 만들 수 있습니다. 위의 각각의 열 백터를 사용해 아래와 같은 (2,0,5,0)을 포함하는 평면이 해임을 알 수 있습니다. 아래 벡터 그림은 4차원 공간이라고 가정합니다.

Solving linear systems with matrices

🎈 계속해서 Reduce Row echelon form의 다른 예제를 풀어보겠습니다.

🎈 위의 예제 또한 위와 동일 방법을 사용합니다. 여러운점은 딱 정확한 공식이 존재하지 않는 것 같습니다. 결국은 Reduce Row echelon form 형태로 만들기 위해 많은 예제를 확인해야하는 것인지가 의문입니다.

Using matrix row-echelon form in order to show a linear system has no solutions

🎈 계속해서 다른 형태의 예제를 학습합니다. 여기선 정답이 없는 예제에 대해 학습하며, 최종적으로 Reduce Row echelon form로 무수한 해가 혹은 해가 존재하는지 안하는지를 확인할 수 있습니다.

🎈 위의 예제의 결과 값을 보면 마지막 행에서 이상한 부분을 확인할 수 있습니다. $0 = -4$ 라는 건 불가능하기 때문입니다. 이는 즉 해를 찾을 수 없다고 해석할 수 있으며, 기하학적으로는 4차원의 공간에서 세 평면은 교차하지 않는 것을 알 수 있습니다. 또한 교차하지 않는다는 것은 평행하다고 이야기할 수 있습니다.

🎈 결과적으로 Reduce Row echelon form의 형태로 해의 존재하는지, 무수히 많은 해가 존재하는지를 알 수 있습니다. 오직 pivot entry로 구성되어있다면 하나의 해가 존재하며, free value가 존재하면 무수히 많은 해가 존재한다는 것을 알 수 있습니다.