[Shorts 선형대수학] Vector dot and cross products 8 (Distance between plane)

👨‍🏫 본 글은 칸 아카데미의 수업을 듣고 정리한 글 입니다.

• Distance between plane

🎈 오늘 평면사이의 두 거리를 구하는 방법을 학습합니다. 본 쳅터는 "Vecotr dot and cross products" 단원에서 배운 내용들을 대부분 사용하는 쳅터입니다. 즉, 기본적으로 앞선 내용을 학습해야 이해가 가능합니다.

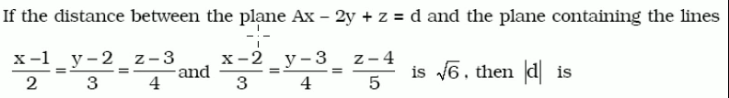
🎈 오늘은 위의 문제를 풀어보면서 두 평면 사이의 거리를 사용해 문제를 해결합니다. $Ax - 2y + z = d$라는 평면과, ${x-1 \over 2} = {y-3 \over 3} = {z-4 \over 4}$과 ${x-2 \over 3} = {y-3 \over 4} = {z-4 \over 5}$ 두 선으로 이루어진 평면을 찾아 거리가 $\sqrt6$ 일때 d 를 찾는 것입니다.

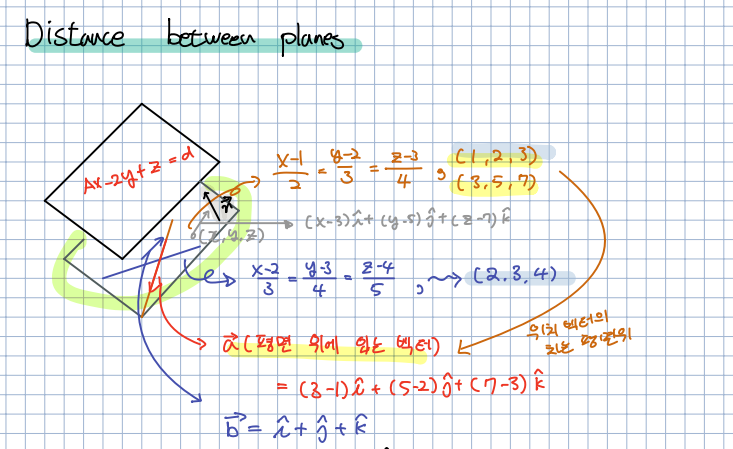
🎈 먼저 두 평면의 거리를 존재하기 위해선, 두 평면이 평행해야만 합니다. 두 평면이 평행한다는 것은 두 평면의 $x, y, z$의 계수 비율이 같아야 합니다.

🎈 또한 두 평면의 거리를 계산하기 위해선, 두 선을 사용해 평면을 구해야합니다. 두 선의 한 점을 찾아서 외적을 구하면 찾을 수 있습니다. 각각의 점을 찾아서 $\vec{a} , \vec{b}$(평면 위에 있는 벡터)를 구할 수 있습니다(위 그림에서 확인할 수 있습니다).

🎈 전에 배웠던 외적의 공식을 사용해 $\vec{a} \times \vec{b}$ 를 구할 수 있습니다. 또한 우리는 이를 평면의 $\vec{n}$(법선 벡터)라는 것은 알 수 있습니다. 이를 사용해 우리는 평면을 구할 수 있습니다. 임의의 $(x, y, z)$점과 $(3, 5, 7)$점의 위치 벡터를 사용해 $\vec{n} \cdot (x-3)i + (y-5)j + (z-7)k = 0$ 임을 알 수 있습니다.

🎈 이를 사용해 $-x + 2y - z = 0$ 라는 평면의 방정식을 찾을 수 있습니다. 또한 두 평면은 평행하기 때문에 $Ax - 2y + z = d$ 에서 $A = 1 $이라는 것을 찾을 수 있습니다.

🎈 결과적으로 한 점과 평면의 방정식을 사용해 거리를 찾을 수 있고, 이 거리가 $\sqrt{6}$ 것을 알고 있기에 $d$를 찾을 수 있습니다.