👨‍🏫 본 글은 칸 아카데미의 수업을 듣고 정리한 글 입니다.

• Matrix vector product
• Introductiono of null space of a matrix
• Null space 2: Calculatin the Null space of matrix
• Null space 3: Relation to linear independence
• Column space of matrix
• Null space and column space basis

---

Matrix vector product

🎈 오늘 행렬연산에 대해 먼저 학습합니다.

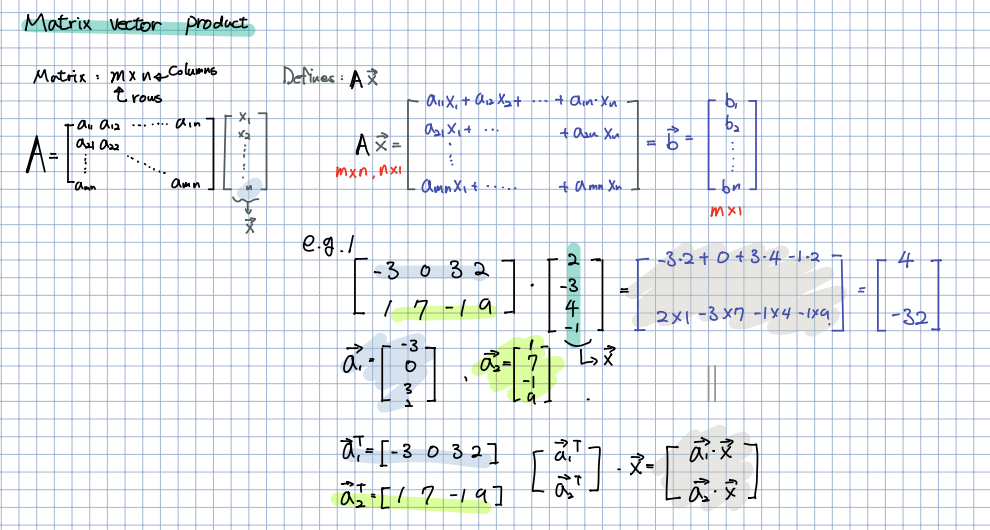
🎈 행렬 연산은 고등학교때 배운 내용과 동일함으로, 크게 설명이 필요하지 않을 것 같습니다.

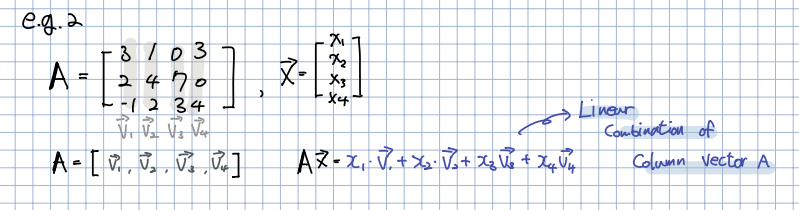
🎈 단, 위의 예제 2번은 한 번쯤은 집고 넘어가야 할 듯합니다. 행렬 $A$와, 벡터 $\vec{x}$의 행렬곱 연산은 A의 열벡터들의 선형결합으로 표현할 수 있었습니다.

Introductiono of null space of a matrix

🎈 이번엔 영공간에 대해 학습합니다.

🎈 이전의 학습한 부분 집합의 정의를 다시 살펴보면, 위와 같이 3가지 조건이 만족해야합니다.

🎈 부분 집합의 정의를 기반으로, 집합 $N$이 과연 부분집합인지 확인하는 작업입니다. 집합 $N$은 $A \cdot \vec{x} = \vec{0}$을 의미합니다.

🎈 결과적으로 위의 전개과정을 차례로 수행하면 부분집합임을 알 수 있습니다. 우리는 집합 $N$을 A의 Null space(영공간) 이라고 부르며, $N(A)$라고 표기합니다.

Null space 2: Calculatin the Null space of matrix

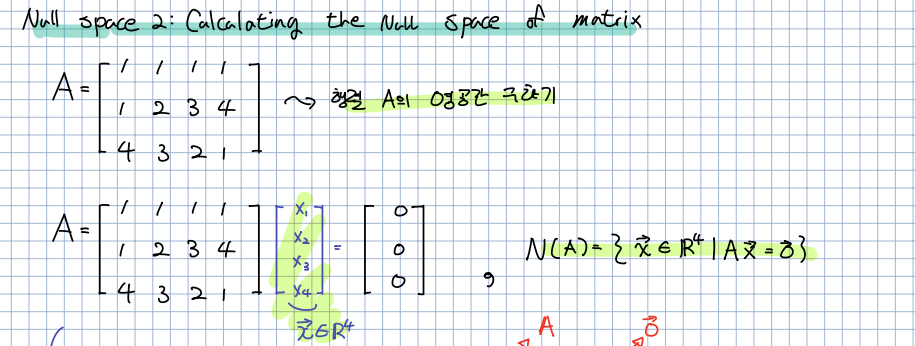
🎈 그렇다면 행렬 $A$가 존재할 때, 위의 집합 $N$을 만족하는 $\vec{x}$를 어떻게 찾을 수 있을까요?

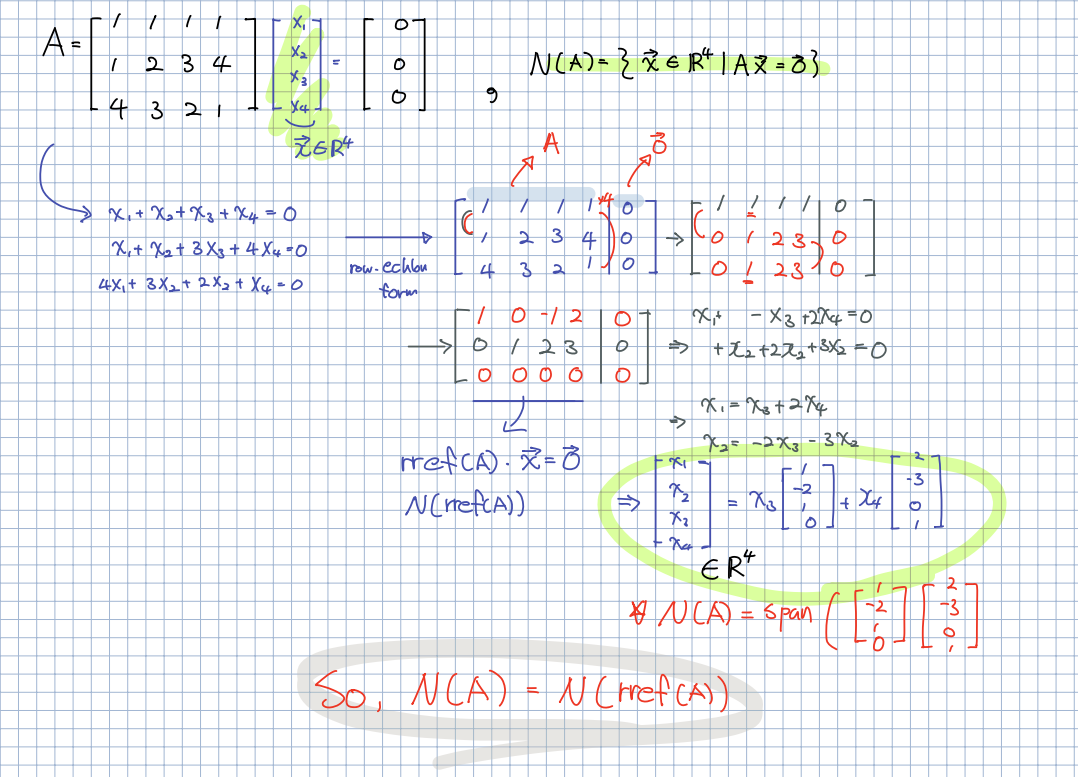
🎈 $\vec{x}$를 찾기 위해 전에 학습한 rref(기약행사다리꼴)를 찾으면 알 수 있습니다. 행렬 A의 rref를 찾으면 항상 영벡터가되는 벡터 $\vec{x}$를 찾을 수 있습니다. 위의 수식을 따라가면 충분히 이해할 수 있을 것이라고 생각됩니다.

🎈 결과적으로 $N(A) = N(rref(A))$임을 위의 수식을 통해 알 수 있습니다.

Null space 3: Relation to linear independence

🎈 선형 독립 그리고 종속과 영공간(Null space)에 관해 학습합니다.

🎈 $m \times n$의 행렬 $A$가 존재하면, 이를 n개의 열이 있고, 각각 m차원 구성하는 열벡터라고 말할 수 있습니다. 행렬 $A$는 $\vec{v}_1$ ~ $\vec{v}_n$로 구성되어 있습니다.

🎈 앞서 배웠던 A의 영공간을 정의하면 위와 같습니다. 그렇다면 행렬 $A$와 $\vec{x}$벡터의 곱은 $\vec{0}$이어야하며, 이는 $x_1 \vec{v}_1 + x_2 \vec{v}_2$ ... $x_n\vec{v}_n = \vec{0}$이며, 이는 선형독립이라고 말할 수 있으며, 오직 $\vec{x}$가 전부 0일 때 해가 성립합니다.

Column space of matrix

🎈 행렬의 열공간에 대해 학습합니다.

🎈 $m \times n$의 행렬 $A$는 $\vec{v}_1$ ~ $\vec{v}_n$로 이루어져있습니다. 각각의 벡터들은 m차원의 실수공간으로 가정합니다. 행렬 $A$의 열공간은 $C(A)$라고 표현할 수 있으며, 이는 $span(\vec{v}_1$ ~ $\vec{v}_n)$이라고 말할 수 있으며, 이는 앞에서 배운 span의 정의를 만족합니다.

🎈 $\{A\vec{x}|\vec{x} \in R^m\}$은 $\{x_1 \vec{v}_1 + x_2 \vec{v}_2$ ... $+ x_n\vec{v}_n|\vec{x}_1, \vec{x}_2, ...\vec{x}_n \in R\}$라고 표현할 수 있으며, 이는 $span(\vec{v}_1$ ~ $\vec{v}_n)$와 같고, $C(A)$라고도 말할 수 있습니다. 이는 새로운 개념이라기 보다는 앞서 배운 내용들을 활용한 것들입니다.

🎈 이를 바탕으로 $A\vec{x} = \vec{b}_1$, $\vec{b}_1$ not $\in C(A)$ 라면 해가 존재하지 않습니다. 적어도 하나의 해가 존재하기 위해선 $\vec{b}_1 \in C(A)$여야 성립합니다. 종합하면 열공간의 열벡터의 모든 선형결합이며, $A\vec{x}$가 가질 수 있는 모든 값입니다.

Null space and Column space basis

🎈 지금까지 rref, 영공간 등 다양한 공식(?)들을 배웠습니다. 하지만 이를 정확히 언제, 왜 사용하는지에 대해선 배우지 않았습니다. 이번 강의를 통해 위의 공식들을 언제, 왜 사용하는지에 대해 학습합니다.

🎈 행렬 $A$의 열공간 $C(A)$의 span이 각각 선형 독립인지 어떻게 알 수 있을까요? 그리고 만약 이 벡터들이 선형 독립성을 가진다면 이는 열공간 $A$의 basis이 됩니다. 우리는 열공간 $A$의 basis를 찾기 위해 먼저 선형 독립인지 여부를 알아야 하며 이는 $N(A) = rref(A)$를 구해 판별할 수 있다고 합니다. "행렬 $A$의 영공간이 0벡터를 가지니다면 행렬 A는 선형 독립성을 가진다"라고 합니다.

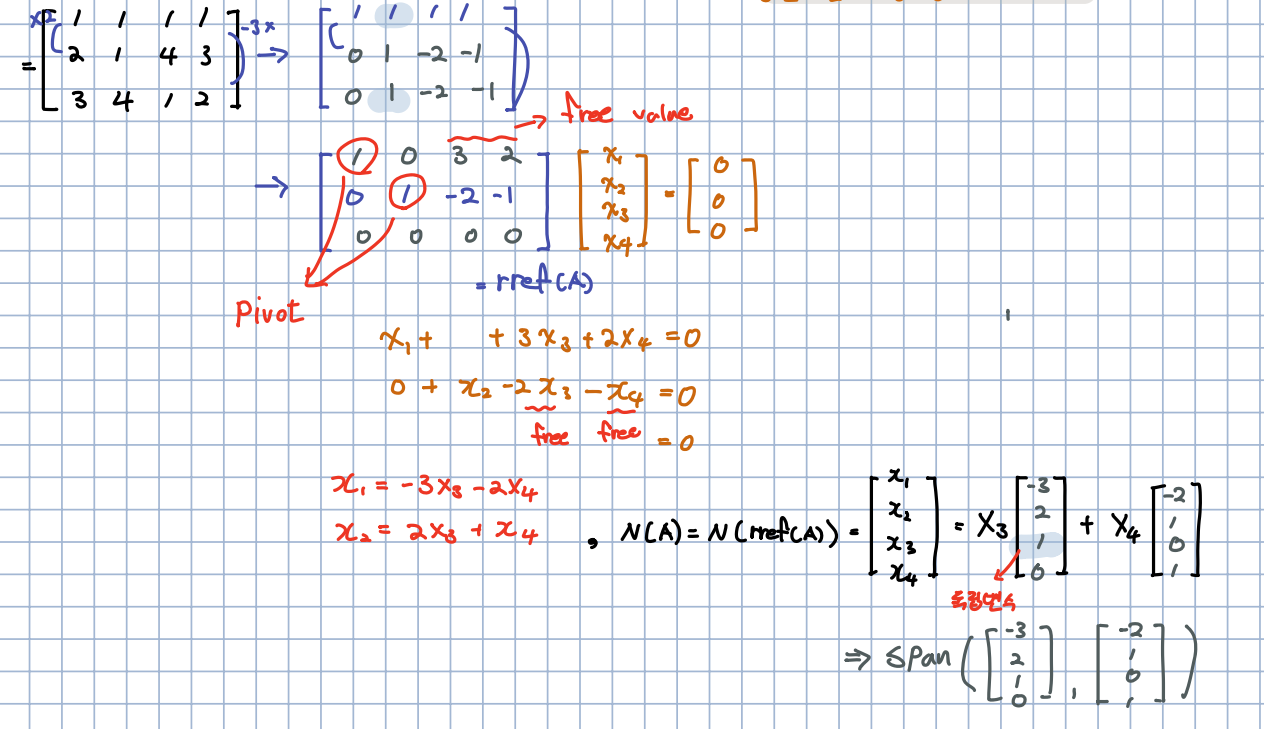
🎈 행렬 $A$가 선형 독립을 판단하기 위해 우리는 $N(A) = rref(A)$ 즉, 행렬 $A$의 영공간이 $\vec{0}$을 나타내는지 증명해야합니다. 행렬 A를 지금까지 배웠던 rref(기약행사다리꼴)의 형태로 나타냄으로써, 각각 pivot, free 값들을 찾을 수 있으며, 이는 $N(A)$를 오른쪽 아래와 같이 $X_3, X_4$로 표현할 수 있습니다.

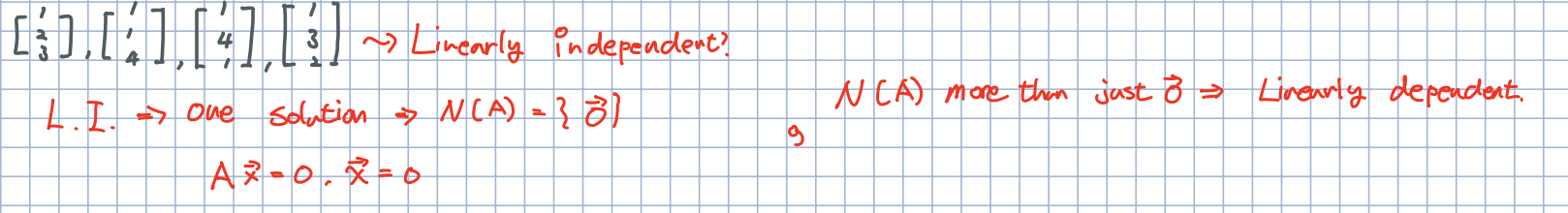
🎈 다시 행렬 $A$의 열벡터들이 선형 독립한다고 이야기 할 수 있을까요? 정답은 아니오 입니다. 이들의 N(A)는 $\vec{0}$를 만족하지 못하기에, 선형 종속 한다는 것을 알 수 있습니다.

🎈 행렬 $A$의 열공간은 선형 독립이 아니기에, basis이지 않습니다. 그렇다면 $C(A)$의 basis는 무엇일까요? 위에서 구한 rref(A)를 사용해 찾을 수 있습니다. free 값에 임의의 값을 지정함으로써 위의 식처럼 각각의 free 값들의 벡터들이 어떻게 첫번째, 두번째 벡터로 표현할 수 있는지 증명할 수 있습니다.

🎈 결과적으로 $C(A) = span(\vec{v}_1, \vec{v}_2)$는 $C(A)$의 basis임을 알 수 있습니다.