👨‍🏫 본 글은 칸 아카데미의 수업을 듣고 정리한 글 입니다.

• Vector dot product properties
• Proving vector dot product properties

Vector dot product properties

🎈 오늘은 벡터의 내적(dot product)에 대해 학습합니다. 내적은 $\vec{a} \cdot \vec{b}$ 같이 표기합니다. 내적의 연산은 $a_1b_1 + a_2b_2 + \cdots + a_nb_n$와 같이 진행되며 결과 값은 스칼라 값입니다.

🎈 우리는 벡터의 길이에 대해 생각해봐야합니다. 고차원이 될수록 길이를 측정하기 어렵기 때문에 길이에 대해 정의할 필요성이 있습니다. $\vec{a}$에 대한 길이를 $\|\vec{a}\|$ 같이 표기합니다. 연산은 위의 사진과 같이 진행되며 결과 역시 스칼라 값입니다.

🎈 $\vec{a} \cdot \vec{a}$를 $\|\vec{a}\|^2$ 이라고 표기할 수 있음을 알 수 있습니다.

Proving vector dot product properties

🎈 다음으로 내적의 성질에 대해 알아보겠습니다. 결론적으로 내적은 곱셈법칙과 교환법칙이 성립합니다. 사실 조금만 생각해보면 당연한 것은데 내적의 결과는 스칼라이기 때문입니다.

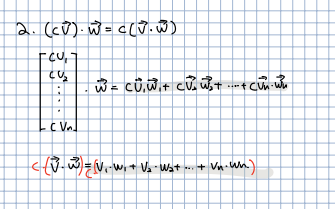
🎈 위의 연산들을 하나씩 따라가면 당연하게 성립하는 것을 볼 수 있습니다.