Gradient Descent - 경사하강법

Gradient Descent - 경사하강법

경사하강법이란?

• 함수의 최솟값을 찾는 최적화 이론(optimization) 기법
• 주로 함수의 파라미터 (베타 값, w 가중치 등) 을 결정할 때 활용
• 파라미터 w이 무엇일 때, Loss function 변화가 가장 작은 지 판단하기 위해
• gradient(기울기) = $g=\frac{\partial L}{\partial w}$ = 가중치 w를 조금 변경했을 때 손실 L이 얼마나 증가하는지 를 나타냄

🔑 경사하강법의 기본 idea: 파라미터를 업데이트 할 때, 손실함수가 가장 빠르게 감소하는 방향으로 파라미터를 업데이트 하는 것 (최소화되어야 하므로)

: 따라서 gradient, 즉 기울기가 0이 되는 곳을 찾는 것이 고전적인 방법이지만, 우리가 사용하는 비선형함수에서는
1. 미분값을 구하고 직접 0을 구하는 과정이 매우 복잡함 (계산과정 복잡)
2. 여러 개의 국소 최저점을 가질 수 있기 때문에 최적값을 찾기 힘들 수 있음
의 문제로, 기울기가 0이 되는 곳을 직접적으로 구하는 것이 아닌
기울기의 “반대 방향”으로 움직임 (증가하는 방향 반대로)

다시 정리하자면.....

1. 기울기의 반대 방향으로 이동

• 기울기(Gradient)는 손실 함수가 증가하는 방향 예를 들어, $g=\frac{\partial L}{\partial w}$ 는 파라미터 $w$를 조금 늘리면 손실 $L$ 이 얼마나 증가하는지 알려줌.
  
• 하지만 우리의 목표는 손실을 줄이는 것 그래서 기울기의 반대 방향으로 이동, 반대 방향으로 가면 손실이 줄어든다!
  

2. 업데이트 식의 의미

경사하강법의 업데이트 식:

각 항목의 의미:

1. $w_{old}$: 이전 파라미터 값 (현재 위치).

   현재 모델이 손실 함수의 어떤 위치에 있는지 나타냄.

2. $g$: 현재 위치에서 손실 함수의 기울기(미분값).

   손실 함수가 이 방향으로 증가하니까, 우리는 반대 방향으로 움직임.

3. $η$ (학습률):

   얼마나 큰 폭으로 이동할 지를 결정하는 값.

   • $η$가 크면 큰 폭으로 이동 (빠른 학습).
   • $η$가 작으면 작은 폭으로 이동 (더 안정적).

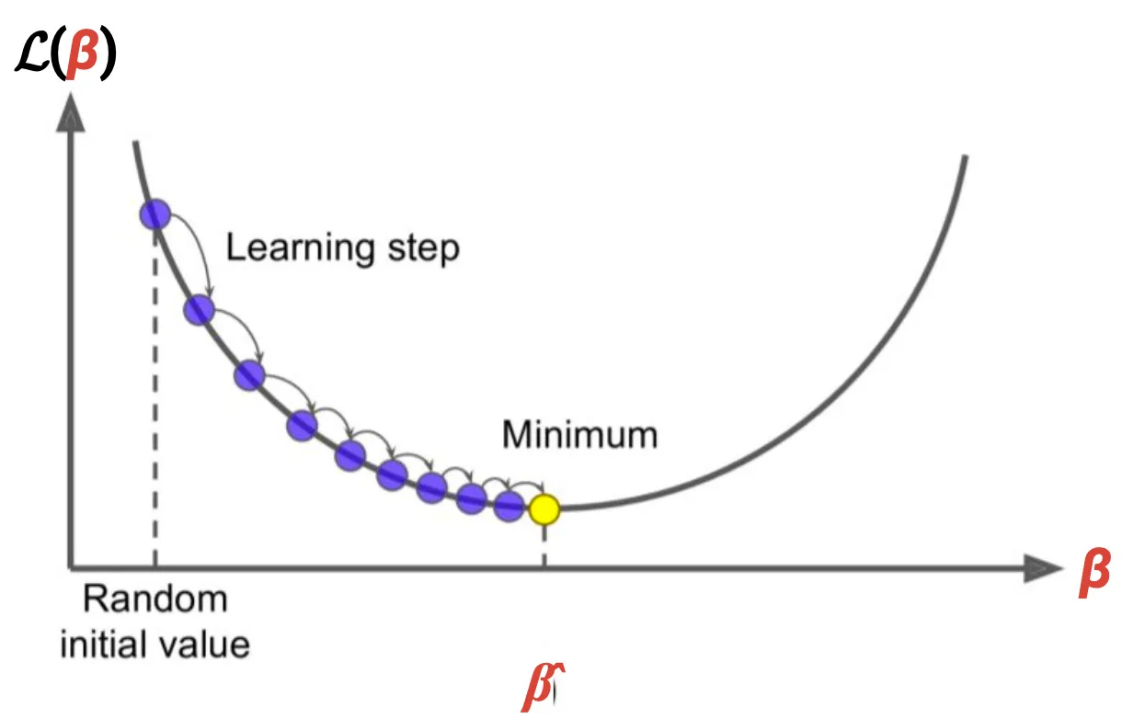
($w$를 $β$ 로 생각하고 보삼)

3. 언제까지 반복?

• 손실 함수의 변화량이 충분히 작아질 때. (수렴 값 미리 설정)
• 기울기가 0에 가까워질 때.
• 최대 반복 횟수에 도달할 때. (epoch, iteration값 채우면)