11/7~11/9 머신러닝 3주차

11/7

⭐0504 실습

✅GridSearchCV

=> 지정된 조합만 보기 때문에 해당 그리드를 벗어나는 곳에 좋은 성능을 내는 하이퍼파라미터가 있다면 찾지 못하는 단점이 있습니다.

✅RandomizedSearchCV

=> 랜덤한 값을 넣고 하이퍼파라미터를 찾습니다.
처음에는 범위를 넓게 지정하고 그 중에 좋은 성능을 내는 범위를 점점 좁혀가면서 찾습니다.

param_distributions = {"max_depth": np.random.randint(3, 100, 10), 
                       "max_features": np.random.uniform(0, 1, 10)}
clf = RandomizedSearchCV(estimator=model, 
                         param_distributions=param_distributions,
                         n_iter=5,
                         n_jobs=-1,
                         random_state=42
                        )
clf.fit(X_train, y_train)

• n_iter: 반복횟수값

• Fitting 5 folds for each of 5 candidates, totalling 25 fits => 5 fold 는 cv 조각 5개를 의미하며 5 candidates 는 n_iter를 의미

• 랜덤포레스트 안에 트리의 개수가 100개가 기본값이라면 그 내부에서도 트리를 100개를 만들기 때문에 디시전트리를 사용할 때보다 속도가 더 오래 걸린다

• CV 기본값 = 5

• cv는 cross validation의 약자로 어떤 조각이 어떤 성능을 냈는지를 알려줍니다.

• cvresults
  pd.DataFrame(clf.cvresults).sort_values(by="rank_test_score")

🎈Q&A

• 7:3 이나 8:2 로 나누는 과정은 hold-out-validation

• hold-out-validation 은 중요한 데이터가 train:valid 가 7:3이라면 중요한 데이터가 3에만 있어서 제대로 학습되지 못하거나 모든 데이터가 학습에 사용되지도 않음. 그래서 모든 데이터가 학습과 검증에 사용하기 위해 cross validation을 진행

• cross validation은 속도가 오래걸린다는 단점이 있기도 하지만 validation의 결과에 대한 신뢰가 중요할 때 사용.
  ex) 사람의 생명을 다루는 암여부를 예측하는 모델을 만든다거나 하면 좀 더 신뢰가 있게 검증이 유리

• hold-out-validation 은 한번만 나눠서 학습하고 검증하기 때문에 빠르지만 신뢰가 떨어지는 단점이 있음. hold-out-validation 은 당장 비즈니스에 적용해야 하는 문제에 빠르게 검증해보고 적용해 보기에 좋음

-> cross validation 이 너무 오래 걸린다면 조각의 수를 줄이면 좀 더 빠르게 결과를 볼 수 있고 신뢰가 중요하다면 조각의 수를 좀 더 여러 개 만들어 보면 된다

🔷점수를 올리고 내리는데 너무 집중하기 보다는 일단은 다양한 방법을 시도해 보는 것을 추천합니다!!

⭐0601 실습 - 캐글 Bike Sharing Demand

• 점수 평가 기준: RMSLE
  -> RMSE와 비슷, 중간에 log L이 있음

• 회귀문제: 공유 자전거 수요예측(매시간 빌려진 자전거 수)

• 데이터 설명(도메인 지식 이해하기)

datetime - hourly date + timestamp
season -  1 = spring, 2 = summer, 3 = fall, 4 = winter 
-> 계절로 1,2,3,4로 ordinal encoding(순서가 있는 값)으로 인코딩 됨
holiday - whether the day is considered a holiday
workingday - whether the day is neither a weekend nor holiday
weather - 1: Clear, Few clouds, Partly cloudy, Partly cloudy
2: Mist + Cloudy, Mist + Broken clouds, Mist + Few clouds, Mist
3: Light Snow, Light Rain + Thunderstorm + Scattered clouds, Light Rain + Scattered clouds
4: Heavy Rain + Ice Pallets + Thunderstorm + Mist, Snow + Fog 
-> weather 는 1이면 맑은 날, 2는 흐린날, 3은 눈,비 오는 날, 4는 폭우, 폭설, 우박 내리는 날
temp - temperature in Celsius
atemp - "feels like" temperature in Celsius
-> 체감온도
humidity - relative humidity
windspeed - wind speed
casual - number of non-registered user rentals initiated
registered - number of registered user rentals initiated
count - number of total rentals

🔷답을 바로 찾기보다는 호기심을 갖자!!

🎈데이터 해석
-> 결측치가 없다, object도 없다
-> casual, registered, count의 평균값에 비해 max 값이 크다
-> 습도와 풍속이 0인 날이 있다
1. 풍속
: 결측치가 없는 줄 알았는데 windspeed에서 1313개나 0값을 가진다
2. 습도
:습도와 대여량에 연관성이 적어 습도에 결측치가 있는 것 같지만 굳이 전처리를 안 해줘도 됨(상관이 커 보인다면 결측치를 전처리 해주면 좋다)
3. 온도&체감온도
: 큰 상관관계를 가짐. 작은 예외가 존재하지만 온도가 높아지면 높아질수록 체감온도도 높아진다
-> 이상치보다는 오류 데이터가 존재한다고 볼 수 있음

✅ RandomForestRegressor

    n_estimators=100,
    *,
    criterion='squared_error',
    max_depth=None,
    min_samples_split=2,
    min_samples_leaf=1,
    min_weight_fraction_leaf=0.0,
    max_features='auto',
    max_leaf_nodes=None,
    min_impurity_decrease=0.0,
    bootstrap=True,
    oob_score=False,
    n_jobs=None,
    random_state=None,
    verbose=0,
    warm_start=False,
    ccp_alpha=0.0,
    max_samples=None,
)

-> 분류 or 회귀일 때 criterion 값을 제외하고 나머지는 같다
-> criterion: {"squared_roor", "absolute_error", "poisson"}

• cross_val_predict는 예측한 predict 값을 반환하여 직접 계산 가능
• 다른 cross_val_score, cross_validate는 스코어를 조각마다 직접 계산해서 스코어만 반환해준다.

✅MAE

• 모델의 예측값과 실제 값 차이의 절대값 평균
• 절대값을 취하기 때문에 가장 직관적임

✅MSE

• 모델의 예측값과 실제값 차이의 면적의(제곱)합
• 제곱을 하기 때문에 특이치에 민갑하다.

✅RMSE

• MSE에 루트를 씌운 값
• RMSE를 사용하면 지표를 실제 값과 유사한 단위로 다시 변환하는 것이기 때문에 MSE보다 해석이 더 쉽다.
• MAE보다 특이치에 Robust(강하다=덜 민감하다)

✅RMSLE(Root Mean Squared Logarithmic Error)

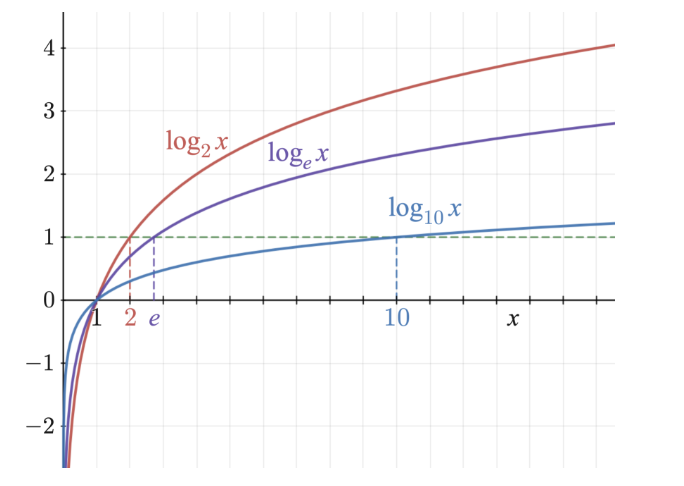
🔷로그 그래프의 기울기를 보면 작은 값에 기울기가 더 가파르고 값이 커질수록 기울기가 완만해 짐

-> 1을 더한후 로그값을 취한 이유: x 가 1보다 작으면 음수가 나오기 때문에 1을 더해서 1이하의 값이 나오지 않게 하기위해
(train은 나올 수 없지만 test는 0이 나올 수 있음)
=> 로그 값 씌우면 sacle값이 줄어듦,
skewed 값이 덜 skewed하게 됨(덜 찌그러지게 된다),
정규분포에 좀 더 가까워짐
np.log의 밑 = e

✒️Q. 로그를 취하기 전에 모든 값에 1을 더해서 가장 작은 값이 될 수 있는 0이 1이 되도록 더해주는 이유는 마이너스 값이 나왔는데 MSE를 계산한다면 어떻게 될까?
✒️A. 의도치 않은 큰 오차가 나올 수 있기 때문에 가장 작은 값이 될 수 있는 0에 1을 더해서 마이너스 값이 나오지 않게 해야 함
==> RMSLE는 RMSE 와 거의 비슷하지만 오차를 구하기 전에 예측값과 실제값에 로그를 취해주는 것만 다름

from sklearn.metrics import mean_squared_log_error

rmsle = np.sqrt(mean_squared_log_error(y_train, y_valid_pred))

ex) 부동산 가격
1) 2억원짜리 집을 4억으로 예측
2) 100억원짜리 집을 110억원으로 예측
Absolute Error 절대값의 차이로 보면
1) 2억 차이 2) 10억 차이
Squared Error 제곱의 차이로 보면
1) 4억차이 2) 100억차이
Squared Error 에 root 를 취하면 absolute error 하고 비슷해짐
-> 비율 오류로 봤을 때 1)은 2배 잘못 예측, 2)10% 잘못 예측

💥RMSE: 오차가 클수록 가중치를 주게 됨(오차 제곱의 효과)
💥RMSLE: 오차가 작을수록 가중치를 주게 됨(로그의 효과)
💥MAE: 가중치 없음(제곱, 로그 둘 다 없음)

---

11/8

• 피처 중요도가 높다고 높은 점수가 나오는 것은 아님
  (피처 중요도란 어느 데이터 요소가 확률값 계산에 중요하게 작용을 했느냐 하는 정도를 나타내는 것)

• 점수가 높아야 좋은 측정 지표의 예시는 정확도를 기반으로 하는 분류의 측정지표인 Accuracy와 회귀 모델에서 독립변수가 종속변수를 얼마나 잘 설명했는지 보여주는 결정계수 (r2 score)등

• 점수가 낮아야 좋은 측정 지표는 에러 기반의 측정 지표인 MAE, MSE, RMSE 등
  => R square score 는 1에 가까울수록 더 좋은 성능을 의미. 예측값과 실제값이 같으면 1. 최대값이 1인데 클수록 좋고. 나머지 회귀의 측정공식은 오차를 측정하기 때문에 낮아야 좋다.

✅상대경로 VS 절대경로

• 상대경로는 현재 경로를 기준으로 하는 경로
  ex) ./ 현재 경로 의미

• 절대경로는 전체 경로를 다 지정하는 경우
  ex) 윈도우 C:부터 시작하는 경로

• 현재 경로에서 ./ 쓰는 것과 아무것도 안 쓰는것과 같은 위치를 나타냄
  -> 절대경로를 사용하면 다른 사람의 컴퓨터에서 동작하지 않기 때문에 되도록이면 상대경로를 사용하는 것을 권장
  🔷가장 추천하는 방법: .ipynb파일과 data 폴더를 같은 위치에 두는 것

• log를 count 값에 적용하게 되면 한쪽에 너무 뾰족하게 있던 분포가 좀더 완만한 분포가 된다

• 데이터에 따라 치우치고(skewed) 뾰족한 분포가 정규분포에 가까워지기도 함

• log를 취한 값을 사용하게 되면 이상치에도 덜 민감하게 됨

# count - kdeplot fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(12,3)) sns.kdeplot(train["count"], ax=axes[0])
# count log1p - kdeplot sns.kdeplot(np.log1p(train['count']), ax=axes[1])

✒️ 왜 정규분포가 되면 머신러닝이나 딥러닝에서 좋은 성능을 낼까?
-> 값을 볼 때 한쪽에 너무 치우쳐져 있고 뾰족하다면 특성을 제대로 학습하기가 어렵기 때문에 정규분포로 되어 있다면 특성을 고르게 학습할 수 있음

• log1p와 같은 표현. 1을 더해주는 이유는 1보다 작은 값에서 음수를 갖기 때문에 가장 작은 값인 1을 더해서 음수가 나오지 않게 하기 위함
  'np.log(train["count"]+1)'

✅np.ex

지수함수

train['count_expm1'] = np.exp(train['count_log1p'])-1
train[['count', 'count_log1p', 'count_expm1']]```
-> expm1을 했더니 로그 계산이 제거되고 원래 값으로 되돌려줌
-> log를 취할 때는 1을 더하고 로그를 취했는데 지수함수를 적용할 때는 반대의 순서대로 복원해야 순서가 맞음
-> np.exp로 지수함수를 적용하고 -1을 해주어야 로그를 취했던 순서를 복원해줌
-> np.exmp1은 지수함수를 적용하고 -1을 해주는 순서로 되어있음

* count == np.expm1(np.log1p()) 같은 값

```fig, axes = plt.subplots(nrows=1, ncols=3, figsize=(12,3))
# count - kdeplot
sns.kdeplot(train["count"], ax=axes[0])
# count log1p - kdeplot
sns.kdeplot(train["count_log1p"], ax=axes[1])
# count, log1p, expm1
sns.kdeplot(train["count_expm1"], ax=axes[2])

• count 값에 대한 기술통계 값과 로그를 취하고 복원한 count_expm1값을 비교했을 때 같은지 확인바람~
  train[['count', 'count_log1p', 'count_expm1']].describe()

❓왜 count에 log를 취하고 다시 지수함수로 복원했을까❓
❗log값으로 예측하고 예측값을 복원하기 위해❗

✒️실무에서는 보통 비즈니스 평가지표를 더 많이 사용. 경진대회나 실습에서 사용하는 평가지표는 모델의 성능을 측정해서 객관화 해보기 위해 사용. 모델을 만드는 목적은 비즈니스 문제 해결을 위해서 이다. 그 모델의 목적이 DAU를 올리는 것이라면 DAU를 측정하고 매출을 늘리고 싶다면 매출액이 늘어났는지, 구매자수가 늘어났는지 등을 평가.

✅RandomizedSearchCV 코드

from sklearn.model_selection import RandomizedSearchCV

param_distributions= {'max_depth':np.random.randint(3,100,10),
                     'max_features':np.random.uniform(0,1,10)}

reg = RandomizedSearchCV(model, 
                         param_distributions= param_distributions, 
                         scoring="neg_root_mean_squared_error",
                         n_iter=10, cv=5, n_jobs=-1,
                         verbose=2, random_state=42)
reg.fit(X_train, y_train)

✅neg_root_mean_squared_error

• neg_root_mean_squared_error 로 되어 있어서 스코어가 음수로 나옴
  rmsle = abs(reg.best_score)

• 추측 : neg_root_mean_squared_error 아마도 정렬을 위해 앞에 음수를 붙여준 것이 아닐까
  ex) Accuracy, R square score 는 큰 값일 수록 좋은 값
• neg_root_mean_squared_error 는 절대값을 적용하였을 때 작은 값이 오차가 작은 값

-> score : neg_root_mean_squared_error 설정
-> score가 음수로 나옴
(음수이기 때문에 절댓값이 작을수록 좋은 성능을 내는 모델)

🔷RMSE와 RMSLE 값이 동일
-> label인 count값에 로그를 취해주었기 때문
-> BUT best_modle로 다시 cross_val_predict를 하면서 cv를 다시 나눠 학습하고 예측해서 점수가 다르게 나올 수 있음

💥 모델 학습과정에서 log1p를 적용해줬기 때문에 답안을 제출할 때에는 expm1을 적용시키고 제출해야 함
df_submit['count']=np.expm1(y_predict)

⭐ 0701 house prices predict 실습

✒️ 캐글 내 권장 튜토리얼을 따라해 보면 예습과 복습에 도움이 된다~!!!!

• 데이터 셋
  : 변수로는 내외관 품질, 화장실의 수, 방의 개수, 수영장 여부, 지붕, 언제 건축이 되었는지 등의 데이터가 있음

✅feature engineering

: 데이터에 대한 지식을 바탕으로 특성(feature)을 생성, 변경 삭제하는 등 조작하여 사용하기 더 유용한 형태로 바꾸는 것을 의미

• feature engineering 분류
  1. 특성 선택
  : 도메인(해당분야) 전문가의 지식이나 특성의 중요도에 따라 일부 특성을 버리거나 선택
  2. 특성 추출
  : 특성을 버리거나 선택하는 것이 아니라 특성들의 조합으로 새로운 특성 생성
  3. 범위 변환
  : 변수의 분포가 편향되어 이상치가 많이 존재하는 등의 변수의 특성이 잘 드러나지 않아 활용하기 어려울 경우 변수의 범위 바꿔주기
  -> 분포 편향: 왜도가 높거나 정규분포와 거리가 멀다, 데이터가 한 쪽으로 치우쳐 있다 를 의미
  4. 변형
  : 기존에 존재하는 변수의 성질을 이용해 새로운 변수 생성
  5. 범주화
  : 연속형 변수 -> 범주형 변수 변환
  6. 숫자화
  : 범주형 변수 -> 연속형 변수 변환

• 데이터 해석
  -> 2000년대에 지어진 집이 많다
  -> MiscVal 데이터가 0에 쏠려있다
  -> 수치가 0인 항목이 많다

✅결측치 구하기

: Feature가 적절한 값을 가지지 못하고 무의미한 값을 갖는 경우
: 데이터 수집 과정에서 누락되거나 원래 존재할 수 없는 데이턴데 구조상 생겼을 수 있음

train_null = train.isnull().sum() train_null[train_null!=0]
train.isnull().sum().sort_values(ascending=False)[:20]
test_null = test.isnull().sum() test_null[test_null>0].sort_values(ascending=False)

train_na_mean = train.isnull().mean()

pd.concat([train_null, train_na_mean], axis=1).loc[train_sum.index]

✅이상치 탐색

: feature에서 일반적인 값 분포에서 벗어나는 경우
: 데이터 수집과정이나 조작 과정에서 잘못 생겼을 수도 있고 예회적으로 수치가 뛰어오를수도 있고
-> 데이터의 해석이나 학습을 방해함
(이상치로 인한 과대적합)

🔷이상치 찾는 방법
1. 값의 범위를 지정하여 범위에서 벗어나는 값을 찾기
2. 데이터를 시각화하여 그래프에서 눈에 띄는 값을 찾기
-> 대상 데이터의 "saleprice"(정답값)값을 산점도로 그려서 이상치 범위를 정할 수 있음

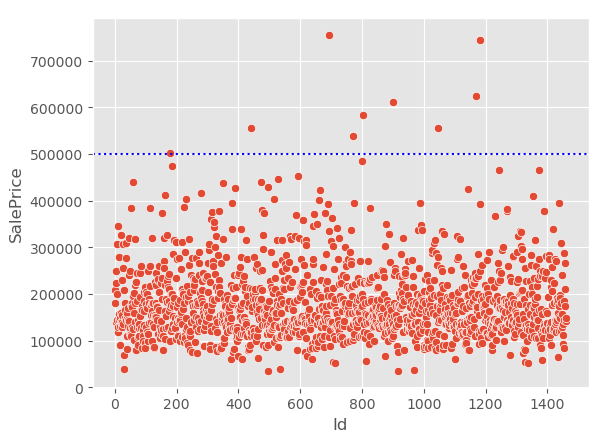
• train의 정답에 이상치가 있다면 어떻게 처리하는게 좋을가???
  -> 정답값이기 때문에 스케일링을 하는게 맞다!
  스케일링을 하면 log를 취했던 것처럼 다시 복원 가능
  ✒️label==target==정답

✅희소값

: numercie feature에서 대부분 값이 갖는 범위에서 벗어난 값 = 이상치
: categorical feature에서 빈도가 낮은 값 = 희소값
-> 데이터를 수집하다보면 자연스럽게 비율이 높고 낮은 값이 생김
-> 희소한 feature가 데이터 해석을 어렵게 하고 머신 러닝 성능을 낮출 수 있음

# object type nunique train.select_dtypes(include="object").nunique().nlargest(10)
# Neighborhood - value_counts train["Neighborhood"].value_counts()
# countplot plt.figure(figsize=(20,5)) sns.countplot(data=train, x="Neighborhood", order=train["Neighborhood"].value_counts().index)
ncount = train["Neighborhood"].value_counts() ncount sns.countplot(data=train, y="Neighborhood", order=ncount.index)

• 희소값에 대해 one-hot-encoding 을 하게 되면 오버피팅이 발생할 수도 있고 너무 희소한 행렬이 생성되기 때문에 계산에 많은 자원이 필요
• 희소한 값을 사용하고자 한다면
  1) 아예 희소값을 결측치 처리하면 one-hot-encoding 하지 않는다.
  2) 희소한 값을 "기타" 등으로 묶어줄 수 있다.

---

11/9

✅피쳐 스케일링

• 트리기반 모델은 정보 균일도를 기반으로 되어 있어서 피처 스케일링은 필요 없음
  -> 트리기반 모델은 데이터의 절대적인 크기보다 상대적인 크기에 영향을 받기 때문에 스케일링을 해도 상대적 크기 관계는 같다

🔷변수 스케일링(=feature scaling)
1. feature의 범위를 조정하여 정규화하는 것
2. 일반적으로 feature의 분산과 표준표차를 조정하여 정규분포 형태를 띄게 하는 것이 목표

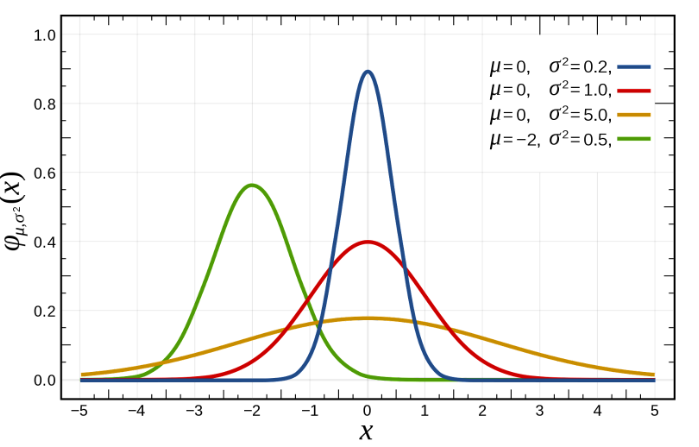
-> 붉은 선이 정규분포 형태

🔷feature scaling이 중요한 이유
1. feature의 범위가 다르면 feature끼리 비교하기 어렵고 일부 머신러닝 모델에서는 제대로 작동하지 않음
2. 스케일링이 잘 되어있으면 서로 다른 변수까지 비교하는 것이 편리
3. 더 빨리 작동
4. 성능 상승
5. 일부 feature scaling은 이상치에 대한 강점이 있음
ex) robust scaling

✒️IQR: interquartile Range로, 상위 75%와 하위 25% 사이의 범위 의미

자주 쓰는 스케일링 기법

✅normalization-standardization(Z-score scaling)

: 평균을 제거하고 데이터를 단위 분산에 맞게 조정
-> 표준 편차가 1이고 0을 중심으로 하는 표준 정규 분포를 갖도록 조정
-> 변수가 왜곡되거나 이상치가 있으면 좁은 범위의 관측치를 압축하여 예측력을 손상시킴
🔷 공식: z=(X-X.mean)/std

✅Min-Max scaling

: feature를 지정된 범위로 확장하여 기능을 변환.
: 기본값은 [0,1]
-> 변수가 왜곡되거나 이상치가 있으면 좁은 범위의 관측치를 압축하여 예측력을 손상시킴
🔷 공식: X_scaled = (X-X.min)/(X.max-X.min)

✅Robust scaling

: 중앙값을 제거하고 분위수 범위(기본값은 IQR)에 따라 데이터 크기 조정
-> 편향된 변수에 대한 변환 후 변수의 분산을 더 잘 보존
-> 이상치 제거에 효과적
🔷 공식: x_scaled = (X-X.median)/IQR

🔷 스케일링 방법 중에서 이상치에 가장 덜 민감한 스케일링 방법: Robust scaling

💥 1. StandardScaler

• 평균 0, 표준편차 1의 특징을 가지고 있음
• 평균을 이용하여 계산해주기 때문에 이상치에 영향을 받는다. (평균: 이상치의 값에 크게 영향을 받기 때문)
  : 평균을 빼주고 표준편차로 나눠줍니다.

💥 2. MinMaxScaler

• 변수 범위를 0과 1사이로 압축해주는 개념
• 이상치를 포함하고 있으면 범위설정에 영향이 가기 때문에 이상치에 의해 영향을 많이 받는다.
  : 0~1 사이값으로 만듭니다.

💥 3. RobustScaler

• 중앙값과 사분위 수를 이용한 스케일링 기법
• StandardScaler와 다르게 중앙값(median)을 이용하기 때문에 StandardScaler, MinMaxScaler에 비해서 이상치의 영향을 덜 받는다.
  : 중간값을 빼주고 IQR값으로 나눠줍니다. 이상치에 덜 민감

✒️ 변수 스케일링은 라이브러리에 저장되어있어 불러오기만 하면 됨!

💥 스케일링을 했을 때 분포가 변하지 않는다. x 축 값을 보면 min-max x값이 0~1 사이에 있고, std => 평균을 빼주고 표준편차로 나눠주고, roubust => 중간값으로 빼고 IQR로 나눠준 결과

💥 트리 알고리즘에서는 절대적인 값보다 상대적인 값에 영향을 받기 때문에 스케일링에 영향을 크게 받지 않지만 다른 알고리즘에서는 스케일링 값을 조정해 주면 모델의 성능이 좋아짐

⭐0701 실습

ss.fit(train["SalePrice"])
-> 오류가 남
ss.fit(train[["SalePrice"]])
->데이터 프레임 형태로 수정해야함

• standardscaler로 스케일링
  (train[["SalePrice_ss"]]) = ss.fit(train[["SalePrice"]]).transform(train[["SalePrice"]]) (train[["SalePrice_ss"]])
  -> StandardScaler의 fit에는 matrix를 넣어주어야 하기 때문에 Series가 아닌 DataFrame으로 넣어줘아함
  -> 그래서 대괄호 2번 감싸기
  🔷 반환값도 matrix 형태이기 때문에 새로운 파생변수를 만들고자 한다면 데이터프레임 형태로 파생변수 만들어줌
  🔷 사이킷런의 다른 기능에서는 fit => predict를 했었지만 전처리에서는 fit=> transform을 사용

✅scaling 코드

1. standardscaling
   ss = StandardScaler() (train[["SalePrice_ss"]]) = ss.fit(train[["SalePrice"]]).transform(train[["SalePrice"]]) (train[["SalePrice_ss"]]) (train[["SalePrice", "SalePrice_ss"]]).head(2)

2. minmaxscaler
   mm = MinMaxScaler() (train[["SalePrice_mm"]]) = mm.fit(train[["SalePrice"]]).transform(train[["SalePrice"]]) (train[["SalePrice","SalePrice_mm"]]).head(2)

3. robustscaler
   rs = RobustScaler() (train[["SalePrice_rs"]]) = rs.fit(train[["SalePrice"]]).transform(train[["SalePrice"]]) (train[["SalePrice", "SalePrice_rs"]]).head(2)

✅transform

• 스케일링을 예시로 fit 은 계산하기 위한 평균, 중앙값, 표준편차가 필요하다면 해당 데이터를 기준으로 기술통계값을 구하고 그 값을 기준으로 transform 에서 계산을 적용해서 값을 변환
  fit 은 train 에만 사용하고 transform 은 train, test 에 사용
• fit 은 test 에 사용하지 않음: 기준을 train으로 정하기 위해서
• 학습을 할 때도 fit은 train 에만 해주는 것과 동일
  ❗ 피처에 fit_trainsform은 train에만 사용!!!
  ❗ test에는 transform만!!
  ❗ test에도 fit을 하게 되면 train.test의 기준이 달라짐!!!
• feature scaling이 잘 됐지만 아직 표준 정규분포 형태는 아님
• 표준정규분포 형태로 만들기 위해 log transformation이 필요
  (log함수가 x값에 대해 상대적으로 작은 스케일에서는 키워주고 큰 스케일에서는 줄여주는 효과가 있음)

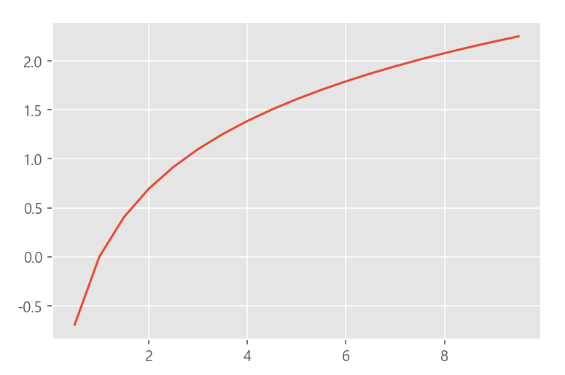
1. log함수는 x값이 커질수록 기울기 완만
2. x값이 작을수록 y의 변화량이 크고, x값이 클수록 y의 변화량은 작다
3. 작은 숫자들 사이의 차이는 벌어지고, 큰 숫자들 사이의 차이는 줄어듬
-> 이미 잘 분포되어 있는 feature의 경우에는 transformation이 불필요할 수 있지만 편향된 feature의 경우 log가 적용된 값은 원래 값에 비해서 더 고르게 분포되어있고
고르게 분포되어있다는 것은 y 값을 예측하는데 더 유용하다는 것을 의미
💥 그래서 정규분포로 만드는게 중요

🔷 같은 컬럼을 fit하고 변환을 시켜준다면 fit과 transfrom을 한 번에 fit_transform으로 쓸 수 있음

train['SalePrice_ss'] = ss.fit(train[['SalePrice']]).transform(train[['SalePrice']])

==

train['SalePrice_ss'] = ss.fit_transform(train[['SalePrice']])

✅기술통계값으로 보는 scaling의 특징

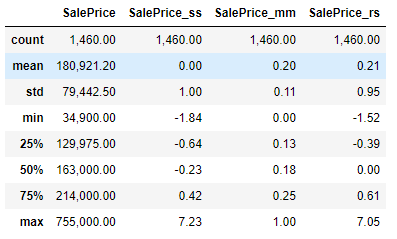
1. standardScaling 특징
: 평균=0, std(표준편차)=1
✒️ Z-score라고도 불림

2. Min-max 특징
: 최솟값 0, 최댓값 1

3. robust 특징
: 중간값(중앙값, 50%, 2사분위수)가 0
: 이상치의 영향을 덜 받음
✒️ robust = 강건하다

✅정규분포

❓ 왜 정규분포로 되어있으면 모델이 더 좋은 성능을 내는걸까?
1. 1.4구간보다 2.3구간이 상대적으로 더 중요
-> 예측하려는 값이 비교적 매우 작거나 매우 큰 값보단 중간값에 가까운 값일 확률이 높다
-> 중간값을 잘 예측하는 모델이 일반적인 예측 성능이 높은 모델
2. 정규분포로 고르게 분포된 값이 예측에 더 유리
-> 예측하려는 값의 분포는 모르지만 정규분포로 고르게 분포시키는 것이 다양한 예측값에 대해 대응 가능케 함

❗ if label(예측하려는 feature)이 편향되어있다면?

• label을 transformation해서 예측 후 반대로 계산하여 출려
  -> log transformation의 경우 log 함수를 이용한 transforamtion
  -> log 함수는 지수함수와 역함수 관계이기 때문에 np.exp()를 이용하면 둘 사이의 변환 가능
  💥 log transformation된 상태로 학습하고 예측 후 예측한 값에 np.exp() 적용하여 출력

✒️ 간격으로 나누기 => 절대평가, 개수로 나누기=> 상대평가 예. 학점

• 표준 정규분포를 이루는지 확인해보기 위해 실습
  train["SalePrice_log1p"] = np.log1p(train["SalePrice"]) train["SalePrice_ss_log1p"] = np.log1p(train["SalePrice_ss"]) train["SalePrice_log1p_ss"] = ss.fit_transform(train[["SalePrice_log1p"]])

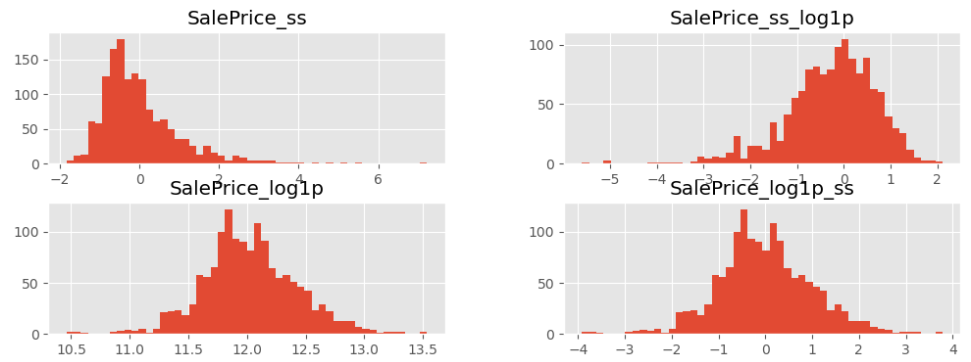
train[["SalePrice_ss", "SalePrice_ss_log1p", "SalePrice_log1p", "SalePrice_log1p_ss"]].hist(bins=50, figsize=(12,4));
  -> log1p ss가 가장 표준 정규분포에 가깝다

🔷 트리계열 모델을 사용한다면 일반 정규분포를 사용해도 무관
그런데 스케일값이 영향을 미치는 모델에서는 표준정규분포로 만들어 주면 더 나은 성능을 낼 수도 있음.
표준정규분포로 만들 때 값이 왜곡될 수도 있기 때문에 주의가 필요
꼭 이런 변환작업을 많이 해준다고 해서 모델의 성능이 좋아진다고 보장할 수 없음
❗상황에 맞는 변환방법을 사용하는 것을 추천❗

✅이산화

: numerical feature를 일정 기준으로 나누어 그룹화 하는 것

🔷 왜 필요할까?
1. 더 직관적임
-> 나이를 개인별로 분석하기 어려울 때 20대 30대 40대로 분석하면 경향이 뚜렷해지고 이해하기 쉬워짐
2. 데이터 분석과 머신러닝 모델에 유리
-> 유사한 예측 강도를 가진 유사한 속성을 그룹화하여 모델 성능을 개선하는데 도움
-> 과대적합 방지

🔷 종류

1. Equal width binning: 범위를 기준으로 나누는 것

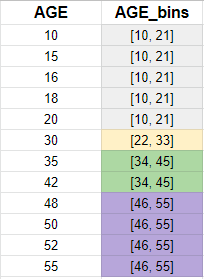
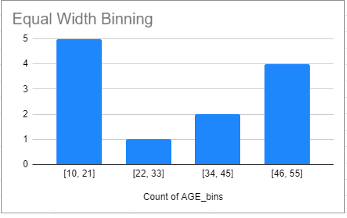
: 가능한 값의 범위를 동일한 너비의 N개의 bins로 나눠줌
-> 편향된 분포에 민감
ex) 절대평가, 히스토그램, pd.cut()

2. Equal frequency binnig: 빈도를 기준으로 나누는 것

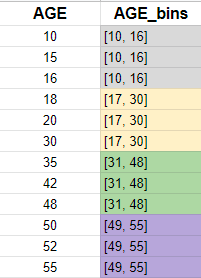
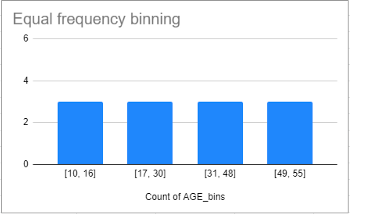
: 변수의 가능한 값 범위를 N개의 bins로 나눠줌. 각 bins는 동일한 양의 관측값을 전달
-> 알고리즘의 성능을 높이는데 도움
-> 임의의 binning은 대상과의 관계를 방해할 수 있음
ex) 상대평가, pd.qcut()

💥 한 분할 안에 몇 개가 들어가는지와 무관하게 전체 수치 범위에 대해 n 분할하는 것이 Equal width binning, 개수를 기준으로 n 분할하는 것이 Equal frequency binning

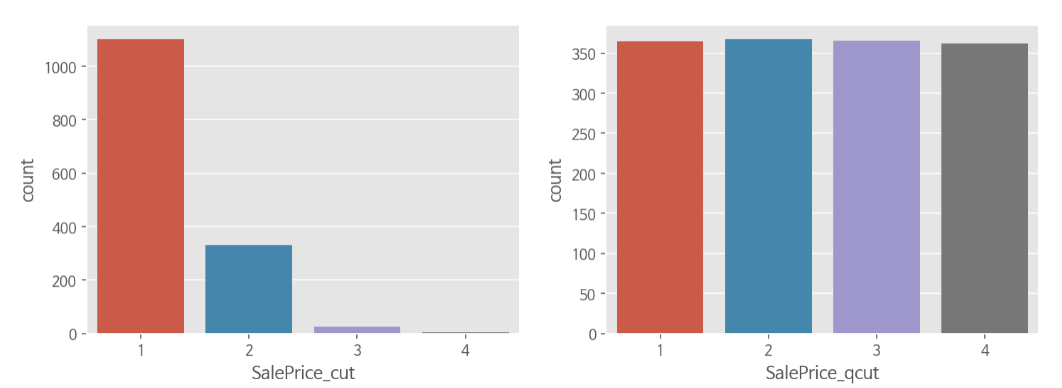
🔷 qcut과 cut

• 코드
  pd.cut(train["SalePrice"], bins=4, labels=[1,2,3,4]) pd.qcut(train["SalePrice"], q=4, labels=[1,2,3,4])

-> pd.qcut은 상대평가와 유사한 개념이기 때문에 pd.qcut으로 데이터를 분할하게 되면 비슷한 비율로 나눠줌(딱 떨어지진 않음)

💥 머신러닝에서 데이터를 분할해서 연속된 수치데이터 -> 이산화 해주는 이유는 머신러닝 알고리즘에 힌트를 줄 수 있고, 너무 세분화된 조건으로 오버피팅(과대적합)되지 않도록 도움을 줄 수 있음

✅인코딩

: categorical feature을 numerical feature로 변환하는 과정

• 데이터 시각화에 유리
• 메신러닝 모델에 유리

✒️ 최근 부스팅3대장 알고리즘 중에는 범주형 데이터를 알아서 처리해 주는 알고리즘도 있지만 사이킷런에서는 범주형 데이터를 피처로 사용하기 위해서는 별도의 변환작업이 필요
-> 부스팅3대장 => Xgboost, LightGBM, catBoost

🔷ordinal-encoding

: categorical feature의 고유값들을 임의의 숫자로 바꿔줌

• 특징

1. 임의의 숫자를 지정할 수 있지만 지정하지 않으면 0부터 1씩 증가하는 정수로 지정
2. 직관적
3. 복잡하지 않고 간단함
4. 단점: 데이터에 추가적인 가치를 더해주지 않음
   -> 순서가 없는 데이터에 적용해주게 되면 잘못된 해석을 할 수 잇음

🔷one-hot-encoding

: categorical feature를 다른 bool변수(0또는 1)로 대체하여 해당 관찰에 대해 특정 레이블이 참인지 여부를 나타냄

• 장단점
  장점: 해당 feature의 모든 정보를 유지
  단점: 해당 feature에 너무 많은 고유값이 있는 경우 feature을 지나치게 많이 사용 (시간 오래 소요)

🔷인코딩 코드 비교

1. MSZoning - .cat.codes => ordinal encoding, 결과가 벡터(1차원형태)
   -> 순서가 있는 명목형 데이터에 사용
   ex) 기간의 1분기,2분기,3분기,4분기
   train['MSZoning'].astype("category").cat.codes

2. get_dummies => one-hot-encoding, 결과가 matrix(2차원 행렬) 형태
   : 순서가 없는 명목형 데이터에 사용
   : 순서가 없거나 크기를 비교할 수 없는 데이터-범주형 데이터에도 사용
   ex) 좋아하는 음료, 주택의 종류, 수업의 종류 등으로
   pd.get_dummies(train['MSZoning'])

🔷sklearn을 이용한 인코딩

from sklearn.preprocessing import OrdinalEncoder

oe = OrdinalEncoder()
onc = OneHotEncoder()

MSZoning_oe = oe.fit_transform(train[["MSZoning"]])

MSZoning_enc = enc.fit_transform(train[['MSZoning']]).toarray()

🔷pandas 인코딩

• pandas 의 get_dummies 를 사용해서 인코딩 하면 train, test 따로 인코딩

• train 학습한 것을 기반으로 test 와 동일하게 피처를 생성해 주어야 하는데 이게 조금 다를 수 있음

• 판다스로 train, test 각각 인코딩 했다면 피처의 수, 종류가 다를 수 있음

• 그런데 학습, 예측을 할 때는 동일한 피처와 개수를 입력해 주어야 함

• pandas 로 인코딩 한다면 set(train.columns) - (test.columns) 이런식으로 비교해서 맞춰주어야 함

• train 에만 등장하는 피처가 있다면 test 에도 동일하게 만들어 줘야함

• 가장 간단한 것은 concat 을 사용하는 방법입니다. 없는 값은 nan 으로 들어가게 되고 다시 train, test 를 나눠주면 됨
  => 처음부터 concat 을 사용하고 나중에 나눠주면 이런 문제를 해결할 수 있음
  => 그런데 test 에만 등장하는 데이터를 피처로 사용하지 말라는 정책이 있을 때 이 방법은 규칙위반일수 있음

• pandas로 인코딩 했을 때 단점: 사이킷런의 원핫인코딩은 train 데이터로만 학습해서 진행하기에 test에만 존재하는 데이터를 인코딩하지 않지만 판다스는 이 기능이 없어서 test셋과 train셋의 고유값을 비교해줘야 하는데, 현실에서 test 데이터는 존재하지 않기 때문에 권장하지 않음

🔷 사이킷런을 사용했을 때 train을 기준으로 fit 을 해주기 때문에 test 는 transform 만 해주면 된다
🔷 train 에는 없지만 test 에만 있는 값은 ohe 되지 않는다
🔷 fit 하는 기준은 꼭 train
-> test 는 미래의 데이터이기 때문에 어떤 데이터가 들어올지 모르기 때문
🔷 경진대회 데이터는 test 가 무엇인지 알고 있지만 일부 경진대회는 test 값을 반영해서 인코딩 하는 것을 금지

✅파생변수

: 이미 존재하는 변수로부터 여러가지 방법을 이용해 새로운 변수를 만들어 내는 것
1. 사칙연산, 최대값, 최소값, 비율 등을 통해서 변수 생성
2. 시간, 지역별 구분, 비율 등으로 생성

• 파생변수 왜 만드는 걸까?

1. 적절히 생성된 파생변수는 데이터의 특성을 더 잘 설명
2. 연관관계를 설명해주는 feature가 없다면 직접 만들어서 사용
3. 더 밀접한 관계를 맺는 feature 생성 가능
   -> feature들 간의 연관관계를 위해

❗ 파생변수 생성으로 데이터 해석이 더 편리해지고 머신러닝 성능이 올라갈 수는 있지만 역효과가 생길수도 있음(마구잡이로 만들면 속도도 느려지고 성능도 낮아짐)

• uniform이란?: 히스토그램을 그렸을 때 어딘가는 많고 적고인 데이터가 있다면 그것도 특징이 될 수 있는데 특징이 잘 구분되지 않는다면 power transform 등을 통해 값을 제곱해주거나 하면 특징이 좀 더 구분되어 보이게 해줌