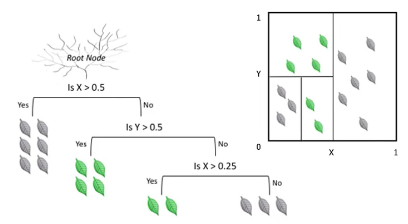
⭐시작 전 복습
- 머신러닝 모형: Loss 함수를 정의하고 그 loss 함수를 최적화 하는 것
- Loss: 실제값과 측정값이 차이를 어떻게 정의하는가 ex)MSE
-> KNN & decision tree는 수학적인 loss 함수는 없지만 majority voting 등을 통해 loss를 최소화해줄 수 있다는 가정을 하고 진행함
-> logistic regression, linear regression 등은 수학적으로 loss function 사용
⭐최적화
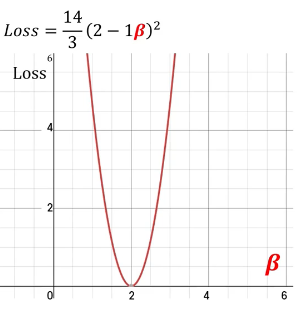
-> loss 함수를 미분해서 구하면 loss 값을 최소화할 수 있는 값이 나옴
-> y=2x : 2일때 최솟값을 가짐
- 우리는 y=2x를 보면 두대일때 최솟값을 가지는 것을 알 수 있지만 컴퓨터는 알 수 없기에 러닝하는 방식을 알려줘야 함
🔷 러닝하는 방식의 핵심은 실제와 예측된 값의 차이를 구해놓고 그 차이가 최소가 되게끔 해주는 '일련의 규칙'을 적용해주면 가장 좋은 모형을 구할 수 있음
=> '일련의 규칙' : Optimization == 최적화
💥 머신러닝에서 러닝은 최적화이다!!!
🔷 사진과 같이 일반화되고 복잡함 함수들이 있는 상황에서 어떻게 optimization을 할 수 있는가?
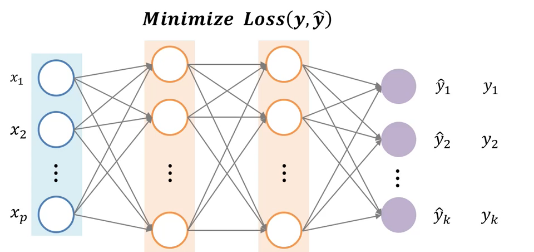
-> 복잡한 neural network
-> 선 하나의 weight or parameter (각각마다 모형의 parameter들이 다 할당되어있는 모습)
💥 Loss 함수는 굉장히 복잡하고 고차원에 있다 -> 암튼 복잡하다
⭐Iterative algorithm-based Optimization
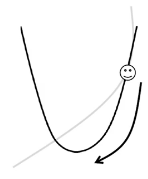
-> 복잡한 능선 위에서 어떻게 하면 효율적으로 내가 가진 함수를 minimize할지 고민하는 과정이 중요
: 산 정상에서 눈을 가리고 산의 가장 낮은 부분까지 잘 내려가는 과정
-> 함수값, 미분결과(기울기=Gradient)는 알 수 있음
✒️ 경사도가 가파르게 낮아지는 방향이 잇으면 한번 가보고, 또 내려가는 부분이 있으면 가보고 (반복적으로)
- 대표적인 종류: Gradeint Descent
⭐경사하강법(Gradient Descent) - 강의용
-> 가파르게 기울기를 해서 함숫값이 굉장히 작아지는 방향을 찾고 그 방향으로 내려가는 방법
💥 경사를 구하고 함숫값을 가장 빠르게 줄일 수 잇는 방향으로 계속 내려간다
-
ex) y=Wx 함수 정의
-W는 보통 랜덤하게 Initialization함
-랜덤하게 Initialize된 상황에서 출발해서 함수를 최소화하는 과정 -
테일러 급수 전개: 모든 일반적인 함수들의 경우에는 무한대에 수렴하는 다항식으로 근사가 가능하다는 것을 이론적으로 연구
-> 이차 다항식을 이용해서 알지 못하는 함수를 근사적으로 표현할 수 있지 않을까??
-> 근사된 이차함수는 미분해서 0 되는 지점을 찾기 쉬움
💥 위의 과정에서 사용하는 수식 표현: Quadratic approximation
🔷 L(w) : loss 함수 - 변수
🔷 L(Wc) : 현재 위치에서의 W값 - 고정된 값
🔷 ▽L(W-Wc) : 기울기
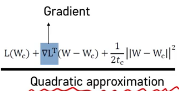
- 미분후
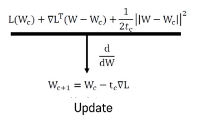
⭐경사하강법(Gradient Descent) - 찾아본것
: 함수의 기울기(경사)를 구하고 경사의 반대 방향으로 계속 이동시켜 극값에 이를 때까지 반복시키는 것
: 딥러닝 알고리즘 학습 시 사용되는 최적화 방법 중 하나
: 예측값과 정답값 간의 차이인 손실 함수의 크기를 최소화시키는 파라미터를 찾는 것
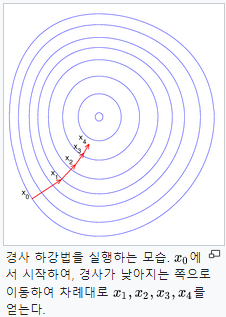
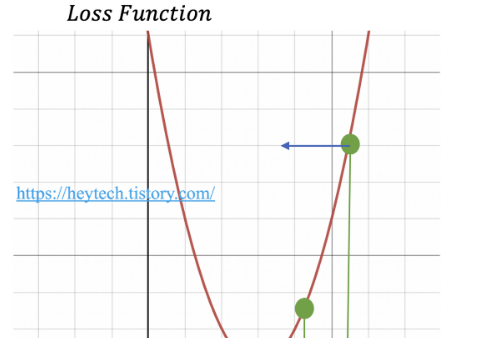
🎈-> 무한 차원상에서도 쓰일 수 있고 무든 차원과 모든 공간에서 적용이 가능
🎈-> 정확성을 위해 극값으로 이동하기 때문에 매우 많은 단계를 거쳐야 함
🎈-> 주어진 함수에서의 곡률에 따라 거의 같은 위치에 시작해도 완전히 다른 결과를 가져올 수 있음
- 수식
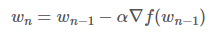
Wn-1을 임의의 가중치로 선정했다고 가정. 최적의 가중치를 찾기 위해서 목표 함수인 손실 함수를 비용 함수 W에 대해 편미분하고, 이를 학습률(Learning rate)과 곱한 값을 앞서 선정한 Wn-1에서 빼줌
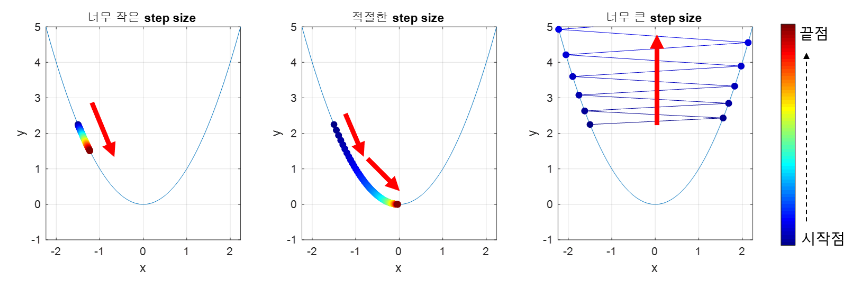
- step size
: step size가 큰 경우 한 번 이동하는 거리가 커져 빠르게 수렴할 수 있음 / 최소값을 계산하도록 수렴하지 못하고 함수값이 계속 커지는 방향으로 최적화 될 수 있음
: step size가 작은 경우 발산하지 않을 수 있음 / 최적의 x를 구하는데 소용되는 시간이 오래 걸림
* 문제점 2개
🎈1. Local Minimum 문제
: 경사 하강법은 비볼록 함수의 경우, 파라미터의 초기 시작 위치에 따라 최적의 값이 달라진다는 한계
🎈2. Saddle Point(안장점) 문제
: 안장점은 기울기가 이지만 극값이 아닌 지점을 의미
: 경사 하강법은 미분이 0일 경우 더이상 파라미터를 업데이트하지 않기 때문에, 이러한 안장점을 벗어나지 못하는 한계
❤️출처: https://heytech.tistory.com/380
❤️출처: K-MOOC 실습으로 배우는 머신러닝
