Overview

Extending WAP

대회에서 나온 WAP 공식은

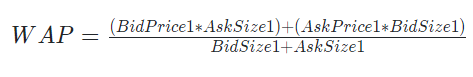
def wap(x) :
    bid_size = 12
    bid_price = 120
    ask_size = 13
    ask_price = 124
    f = -bid_size*np.log(x-bid_price) - ask_size*np.log(ask_price-x)
    
    return f

해당 함수의 최소값을 나타내는 x 값을 공식화 한 것.

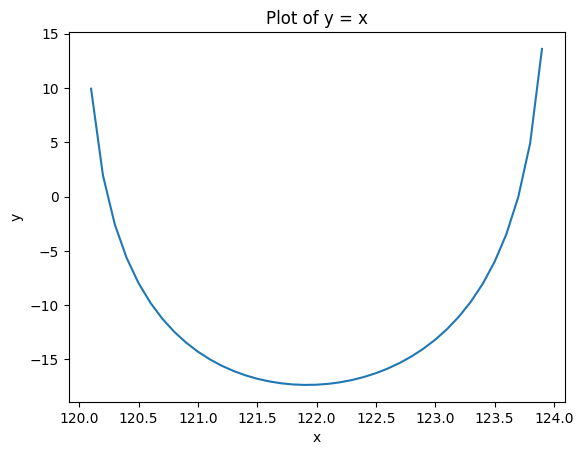
따라서 호가의 깊이에 따라 WAP Feature 개수를 늘릴 수 있다.

위 공식에서는 log 함수에 따라 WAP를 계산하였는데,
lim x->0 일 때, inf로 발산하는 함수 중

$x^{-k}$ : (x는 닫힌 구간 [bid, ask]에서의 주가 k는 호가 깊이)
위 함수를 사용해도 WAP를 구할 수 있다.

f = bid_size*((x-bid_price)**-2) + ask_size*((x-ask_price)**-2)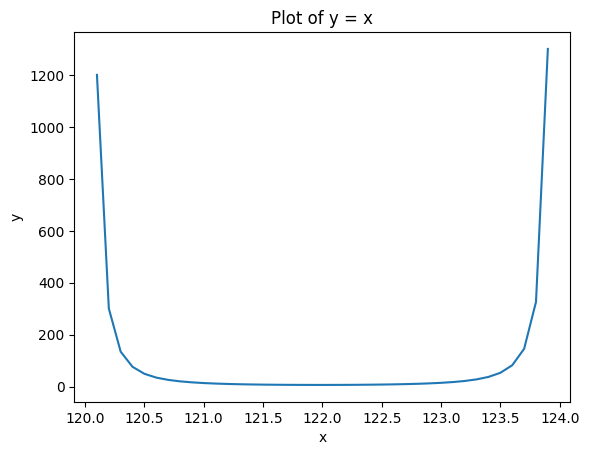

이러한 특징을 가지는 함수를 여러 개 찾아 WAP 값들을 여러 개 만드는 과정을 하였는데, 해당 features들은 performance에 큰 영향을 주지는 못했다고 함.

Defining Liquidity

WAP를 계산하면서 새로운 특징을 고안해 냈는데, 바로 Liquidity 유동성이다.

금융에서 유동성 개념은 자산을 얼마나 빨리 현금화 할 수 있느냐를 의미하는데, 여기서 유동성은 내가 해당 자산을 원하는 가격에 바로 얼마나 구매할 수 있는가로 해석하면 될 것 같다.

유동성을 수치화하려면 3가지 가정이 필요한데, 다음과 같다.

• bid-ask spread가 가까울수록 (값이 작을수록) 유동성이 높다.
• order sizes가 높을수록 유동성이 높다.
• adding additional orders to the book always increases liquidity???

위에서 구한 WAP를 동일한 식에 적용시켜 Liquidity를 계산한다.
liq_1 = sum_i[ bid_size_i/(wap_1 - bid_price_i) + ask_size_i/(ask_price_i - wap1)]

Question

• sum_i 의 의미 ??
• Liquidity 계산식에 위 3가지 가정이 들어가 있는지?
• Liquidity를 Redefine 한다면?

Trade Volume Per Liquidity (TVPL)

Liquidity 자체만으로도 괜찮은 특징이지만,
Trade Volume을 Liquidity로 나눈 TVPL 특징도 volatility와 높은 상관계수 (0.88)를 나타내고 있음.

둘의 관계를 더 살펴보자면, Trade Volume은 매우 Noise가 있는 데이터이고, 그에 반해 Liquidity는 상당히 Stable한 데이터이다.

따라서 Trade Volume 데이터는 full time window 혹은 대부분의 데이터를 다 다뤄야하지만, Liquidity 최근 일부의 데이터만 사용해도 된다.

Question

• 마지막 부분을 어떻게 코드상으로 구현했는지??

FAQ

• LGBM을 Ensembling 예측에 사용하지 않고, 선택한 일부만 MLP 모델에 사용한 이유?

LGBM을 사용하더라도 Performace에 큰 변화는 없었음

• 4 fold로 학습한 2개의 MLP를 사용하였고, 이 둘은 feature 개수가 190개냐 LGBM에서 추출한 40개의 중요한 특성이냐의 차이인데, 그런 선택을 한 이유?

40개 모델은 regularization/ dropout이 적지만 원래 이 방식을 따를 계획이었다.

• 4등 솔루션과 비슷하게 target / current_rv 으로 target을 변경한 이유

Target volatilities span a couple orders of magnitude which might make learning more difficult, volatility ratios are more compact.

Target volatilities가 몇 배에 달하는 범위이기 때문에 모델 학습이 어려워 target를 수정하여 압축하였다.

Rescaling means I can use the log() of features without the NN having to approximate an exponential curve over many octaves.

???

The target ratio is much more correlated between stock ids than the raw target. This is likely important when combining stock ids.
수정한 target이 기존에 비해 stock_id들 간에 상관관계가 더 강할 가능성이 있고, stock_id를 합칠 때 아주 중요하다??

• 대부분의 모델들이 stock 하나에 결과 값 하나 이런 식으로 작동하는데,
  이 풀이에서는 112개의 주식이 input으로 한 번에 들어가 112개의 realized volatilities를 계산

이후 내용은 봐도 잘 이해가 가지 않아 일단 보류..