정적 해싱

정적 해싱은 해시함수가 레코드의 search key를 고정된 버킷 집합에 매핑하는 방법이다. 버킷이란 하나 이상의 엔트리를 저장하는 저장공간으로 일반적으로는 하나의 디스크 블록과 크기가 같도록 설정한다. 정적 해싱을 사용하여 레코드를 조회하기 위해서 DBMS는 찾고자 하는 search key값을 해시함수에 넣어 레코드(혹은 인덱스 엔트리)가 포함된 버킷의 주소를 얻는다. 이때 버킷에 인덱스 엔트리가 들어가면 해시 인덱스, 레코드가 들어가면 해시 파일구조로 구분한다.

해시함수는 조회뿐만 아니라 레코드를 삽입, 삭제할 때에도 레코드의 위치를 찾기 위해 사용된다. 그런데 해시함수를 사용하면 서로 다른 두 search key값이 하나의 버킷으로 매핑되는 collision이 발생할 수 있기 때문에 레코드의 위치를 찾을 때에는 해시 함수를 통해 버킷의 주소를 얻은 뒤, 버킷 내부에서 순차적으로 탐색하여 원하는 레코드를 찾는 작업이 필요하다.

Bucket Overflow

버킷 오버플로우란 해시인덱스 혹은 해시파일의 버킷에 엔트리가 가득 찬 상황에서 해당 버킷에 엔트리가 추가되는 경우로, 충분하지 않은 버킷개수 혹은 레코드의 편향된 분포로 인해 발생한다. 레코드가 편향되어 분포하는 경우는 다시 여러 레코드가 동일한 search key값을 가지는 상황과 해시함수 자체가 편향된 결과를 내는 경우로 나눌 수 있다.

버킷 오버플로우는 여러 방법으로 줄일 수는 있지만, 해시함수를 사용하면 버킷 오버플로우를 완전히 없애는 것은 불가능하기 때문에 오버플로우 버킷을 활용하여 문제를 처리할 수 있다.

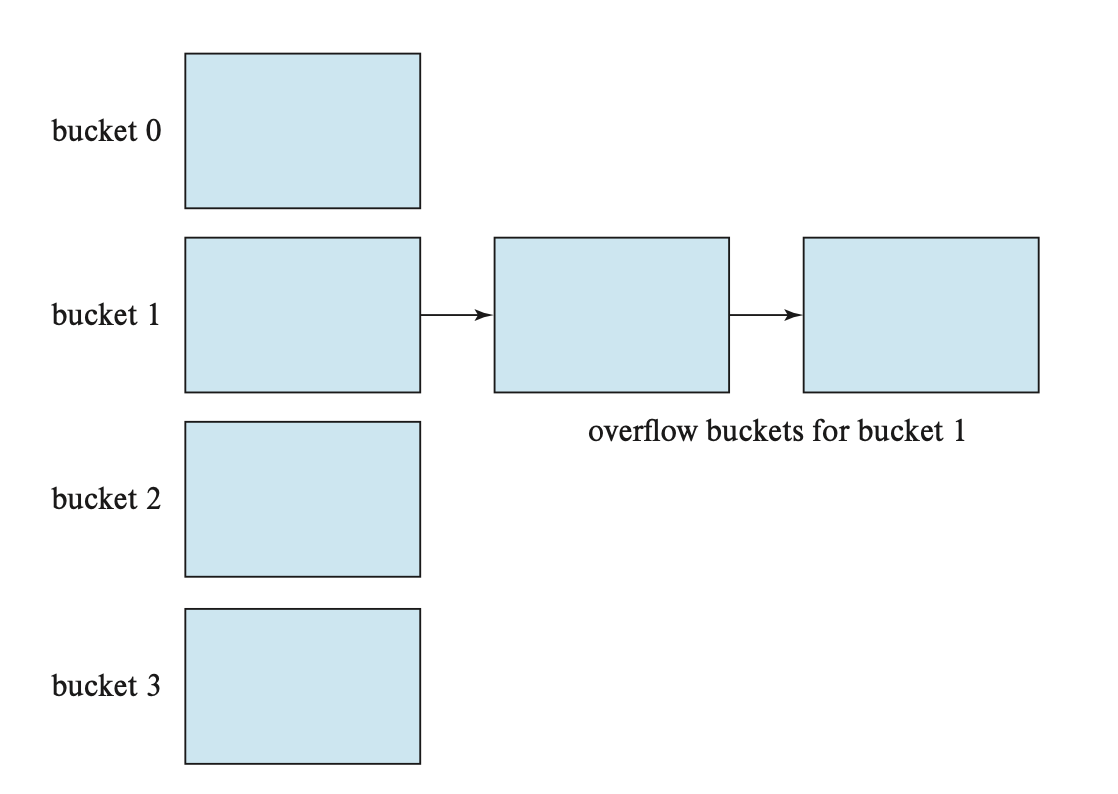
가득 찬 버킷에 엔트리가 추가되어 오버플로우가 발생하면 새로운 버킷을 하나 생성하여(오버플로우 버킷) 연결 리스트로 기존 버킷과 연결한다. 이 방법을 Overflow chaining혹은 Closed addressing이라고 한다. 이와 달리 Open addressing방법은 동일한 상황에서 오버플로우 버킷을 새로 만들지 않고 다른 버킷의 빈자리에 엔트리를 저장하는 방법으로 일부 어플리케이션에서 사용하는 방법이지만, 삭제연산이 비효율적이기 때문에 데이터베이스 환경에는 적합하지 않다.

해시 인덱스

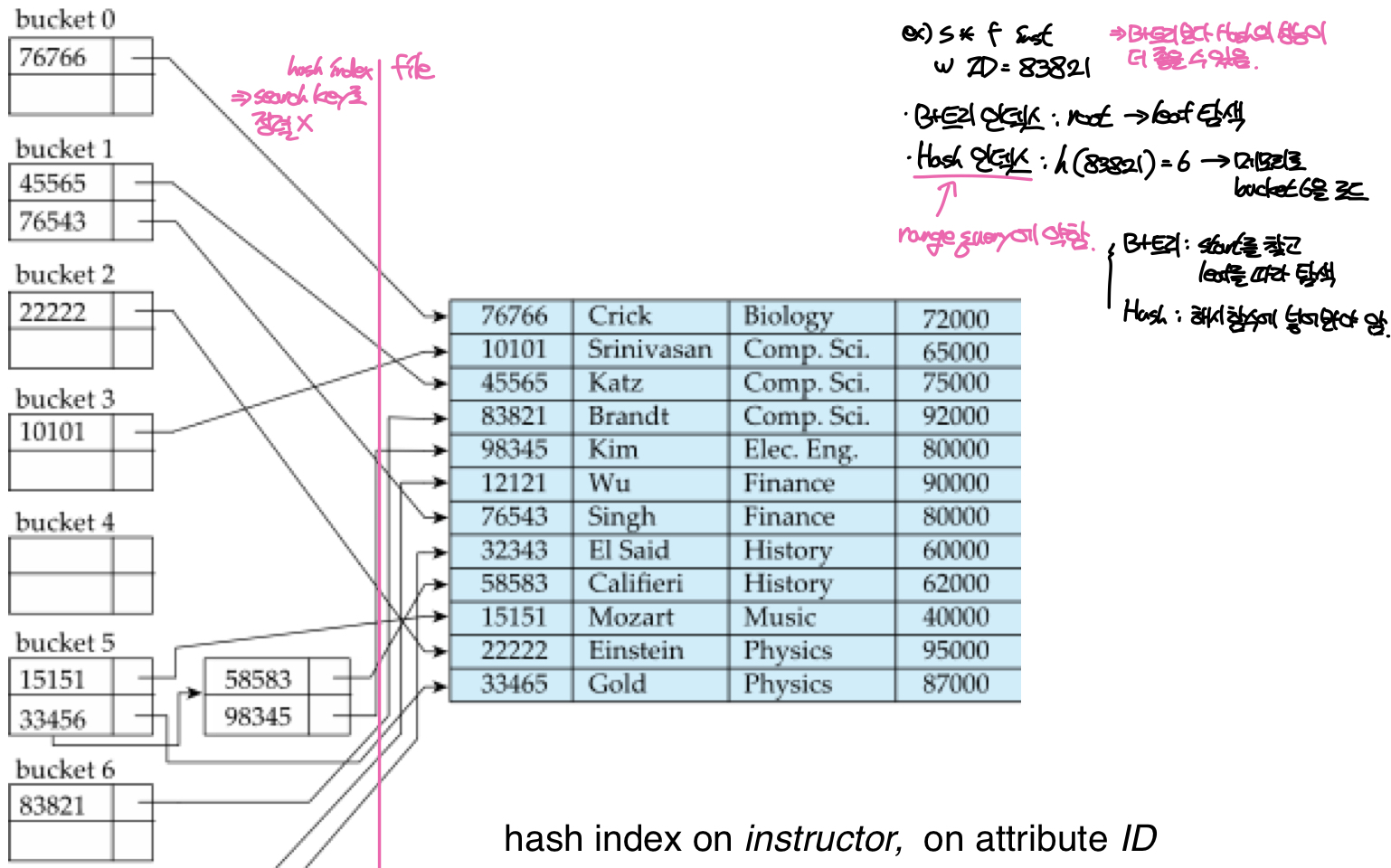
해시 인덱스는 해시 함수를 사용한 인덱스 구조로, 각 버킷에 인덱스 엔트리(search key + pointer)가 저장된다. 해시 인덱스와 B+트리 인덱스를 비교했을 때, 단일 조건으로 레코드를 찾는 쿼리에서는 해시 인덱스의 조회 속도가 더 빠를 수 있다. 예를 들어 select * from TABLE where id = 12345 라는 쿼리문을 실행하면 B+트리 인덱스에서는 root부터 leaf까지 탐색하며 디스크 블록을 메모리로 올려야 하기 때문에 최소 트리의 높이만큼 I/O작업이 수행된다. 하지만 해시 인덱스에서는 키값을 입력으로 해시함수를 돌려 나온 버킷을 바로 메모리로 로드하면 되기 때문에 한번의 I/O작업으로 조회가 끝날 수 있다. 단, 버킷 오버플로우가 많이 발생하여 체인이 길어지는 경우는 해시 인덱스의 조회속도가 더 느려질 수 있다.

또한 해시 인덱스는 Ordered index와 달리 인덱스가 search key를 기준으로 정렬되어있지 않기 때문에 range query에 적합하지 않다는 단점이 있다. B+트리 인덱스에서 range query를 처리하기 위해서는 쿼리의 시작점을 찾고 leaf node를 따라 순차적으로 이동하다가 마지막 레코드를 만나면 종료하는 방식이었는데, 해시 인덱스에서는 해시 함수에 search key를 넣어보기 전까지 해당 레코드의 위치를 알 수 없기 때문에 범위 내의 모든 search key에 대해 해시 함수를 돌려야 한다는 문제점이 있다.

해시 파일 구조

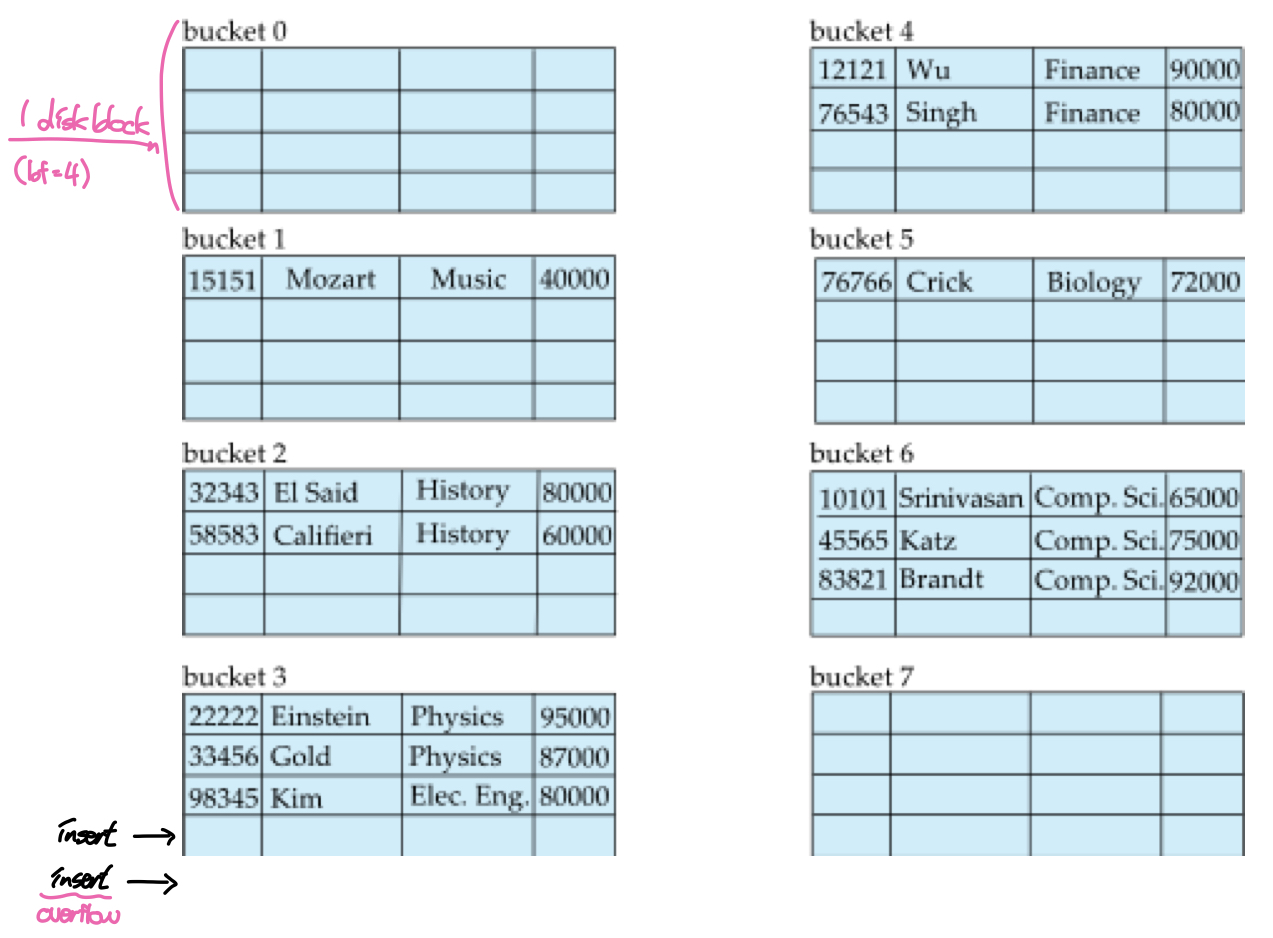
해시 파일 구조는 각 버킷에 인덱스 엔트리가 아닌 실제 레코드를 저장하는 파일구조이다. 각 버킷은 일반적으로 하나의 디스크 블록으로 구성되고, search key를 해시함수에 넣으면 해당 레코드가 저장된 버킷의 주소가 나온다.

동적 해싱

정적 해싱의 문제점

정적 해싱은 고정된 크기의 버킷 주소공간을 사용하기 때문에, 시간이 지남에 따라 데이터베이스가 확장되거나 축소되면 효율이 떨어진다는 장점이 있다. 예를 들어 최초 버킷의 수가 너무 적으면 오버플로우가 많이 발생하기 때문에 성능은 저하된다. 반대로 최초 버킷의 수가 많으면 초기에 버킷공간이 낭비되고, 데이터베이스에 삭제연산이 많이 발생할 때에도 공간이 낭비된다는 단점이 있다.

이를 해결하기 위해서 파일 재구성을 통해 주기적으로 새로운 해시함수를 통해 파일의 구조를 바꿀 수 있지만, 비용이 비싸고 파일을 재구성하는동안 서비스가 중단된다는 문제가 있다. 따라서 좀 더 나은 해결방법으로는 동적 해싱을 사용하여 버킷의 수를 유동적으로 늘릴 수 있도록 하는 방법이 있다.

동적 해싱

동적 해싱은 파일이 성장함에 따라 버킷을 확장하는 방법으로, 대표적으로 Linear Hashing과 Extendable Hashing이 있다. 전자는 해시 함수 자체를 확장하는 방법으로 예를 들어 초기에 해시함수로 mod N을 사용하다가 데이터베이스에 레코드가 많아지면 해시함수에 mod 2N을 추가하여 0 ~ N-1번 버킷은 mod N으로 관리하고 N ~ 2N-1번 버킷은 mod 2N으로 관리한다. 후자는 버킷을 디렉토리 구조로 구성하는 방법으로 데이터베이스에 레코드의 수가 많아지면 디렉토리 번호를 1bit 추가하여 두배로 늘리고, 오버플로우가 발생한 디렉토리에만 버킷을 추가한다.