Grape: Knowledge Graph Enhanced Passage Reader for Open-domain Question Answering

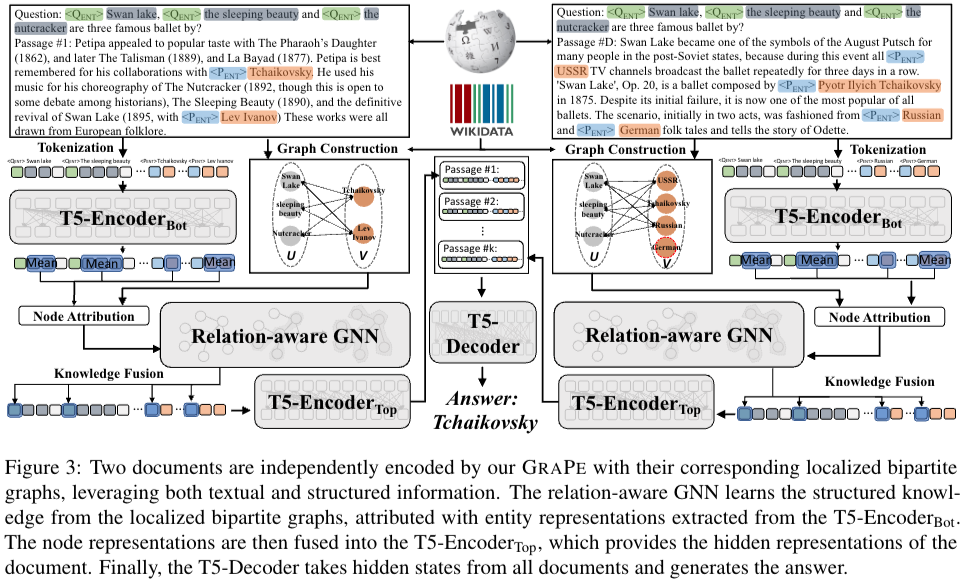
Abstract, Introduction

기존 그래프를 이용한 방식은 복잡한 관계(entities)를 캡처하는데 어려움이 존재하마. 이를 바탕으로 생성할 때 모순적인 facts를 생산한다. 본 논문은 ODQA(open domain question & answer) 작업에서 reader의 performance를 향상시키려는 시도를 하였다.
1. construct localized bipartite graph: entity embeddings를 reader model intermediate layer에서 추출한다. 그런다음 GNN에서 relational knowledge를 학습시킨다.

retriever model은 관련된 passage를 가져오려고 하고 reader model은 final answer을 위해 passage를 받아 추론작업을 진행한다.

본 논문에서는 기존 SOTA 모델인 FiD model도 모순적인 답변을 생산할 수 있다고 언급한다.

이러한 문제가 생기는 원인은 reader model이 factual evidence를 잘 찾지 못하기 때문이라고 언급하면서 저자들은 KG(knowledge graph)에 있는 factual 구조를 사용해 reader모델을 improving시키려고한다.

앞서 말한 bipartite graph를 만들기위해 question과 passage의 각 pair에 대해 각 node, edge representation을 만들어 줘야한다. node representation은 reader model에서의 중간 Layer에서 extracte시킨 것으로 초기화 해서 만든다.

다음으로 node와 relation을 가지고 GNN을 학습시킨다. 그리고 GNN모델을 reader model의 hidden state 에 던져준다.
본 논문 저자는 해당 논문이 첫번째로 KG를 이용한 passage reader의 능력을 향상시킨 작업이고 3개의 dataset에서 SOTA reader를 달성했다고 주장한다.

Related Work

Text-based open-domain QA

retriever-reader architecture들은 고전적으로 TF-IDF, BM25 등의 모델을 사용해 검색된 passage를 매칭시킨 후 가져오했다. DPR같은 경우는 dense contextualized vectors를 passage indexing에 사용하는 작업을 진행하였다. 비슷하게 학습전략들이 다양하게 있으며, passage re-ranking, 또는 generating passage등의 논문들이 reader의 능력을 올릴 수 있게 하는 논문들이 나왔다. 이러한 작업은 정확한 relation을 뽑아낼 수 없다는 단점이 존재한다.

KG-enhanced methods for open-domain QA

최근 연구에서는 knowledge graph(KG)를 retriever-reader pipline에 넣으려는 시도가 존재한다. 예를들어 Unik-QA는 구조화된 KG triples와 비구조화된 text를 merge시켜 unified index로 만드려는 작업을 진행했다. 이를 통해 retrieved evidence는 더 많은 knoledge를 커버할 수 있게 된다.
Graph-Retriever, GNN-encoder는 passage-lebel KG relation을 더잘 검색할 수 있는 연구가 진행되었다. KAQA는 KG realtion에 대한 re-ranking 을 진행한 연구이다.

논문의 저자는 이러한 방식들은 retrieved passage의 성능을 높이고 이를 reader model에 passing하는데에 집중되어 있다고 말한다. 이는 여전히 factual error가 존재할 수 있다고 지적한다.

해당 논문에서는 GRAPE라는 KG를 이용해 reader model performance를 향상시키는 방식을 처음으로 제안한 논문이라고 한다.

Proposed Method: GRAPE

DPR을 이용해 top-k relevant passage를 wikipedia에서 가져오게한다. → 가져온 passage를 localized bipartite graph를 구성하게 한다. 구조화된 graph는 사실에 대한 entity로 구성되어 있다 풍부한 지식을 다룰 수 있게 된다. 마지막으로 구조화된 graph의 facts는 GNN을 통해 relation을 학습하게 되고, passage에 있는 entities의 token-level representation으로 fused 된다.

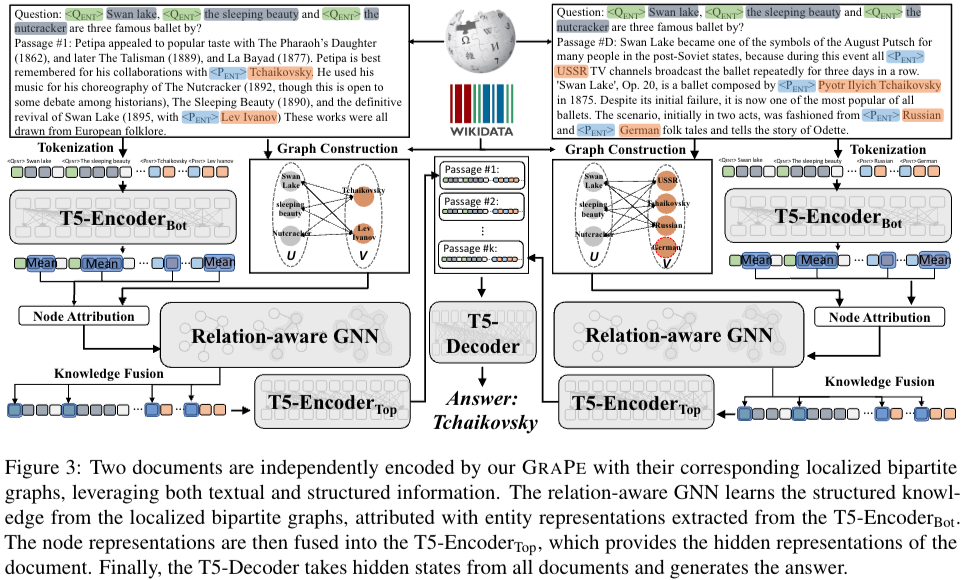
Passage Retrieval

주어진 K개의 passage에서 retrieval의 목적은 저차원의 dim vector로 맵핑시키는 것이다. 이는 효율적으로 top-k개의 관련된 passage를 가져올 수 있게한다. DPR 방식을 이용해 ranking score를 만들어서 top k개의 관련 passage를 가져와 reader모델에게 주는 작업을 진행한다. 본 논문에서는 2개의 $<P_{ENT}>, <Q_{ENT}>$special token을 만들어 사용했다. 이는 reader 모델에서 중요한 역할을 한다.

KG-enhanced Passage Reader

• Graph Construction
  

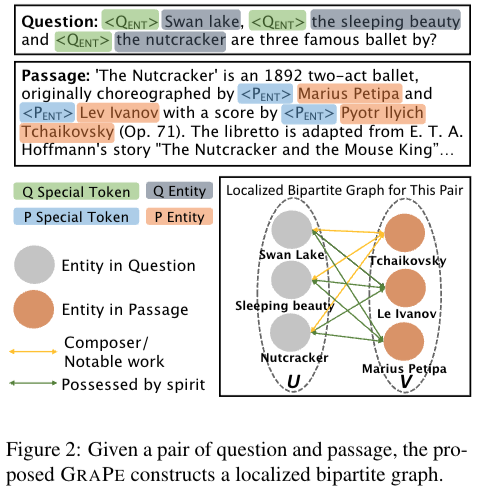
각 question-passage pair에 대해 KG를 통해 localized bipartite graphs를 만들기위해서 먼저 KG는 $\left\{ (e_h, r, e_t) \right\}$의 세트로 정의된다. 각각 head entity, relation, tail entity를 의미한다. Fig2의 예시와 같이 question-passage pair에서 ballet(fig2에 질문)에 대한 사전 정보 없이 정확하게 매칭시킬 수 있다..(?)
이러한 KG triplets로부터 relational fact fusing 하면서 reader모델은 사실을 분명하게 이해하고 ODQA task에서 성능이 증가하게된다.
bipartite graph를 $G = (\mathcal{U}, \mathcal{V}, \mathcal{E})$이라고 할때 u,v노드쌍이되고 나머지는 relation을 의미하게된다. u,v node 각각 question, passage에서 나온 entity를 의미한다.

• Factual Relation Fusion
  GRAPE 는 localized bipartite graphs만들어진 것으로부터 구조화된 knowledge를 reader로 fuse시키는 작업이 진행된다. 본 논문에서는 FiD를 backbone architecture로 사용하고 T5모델을 통해 encoding 과 decoding을 진행한다.
  

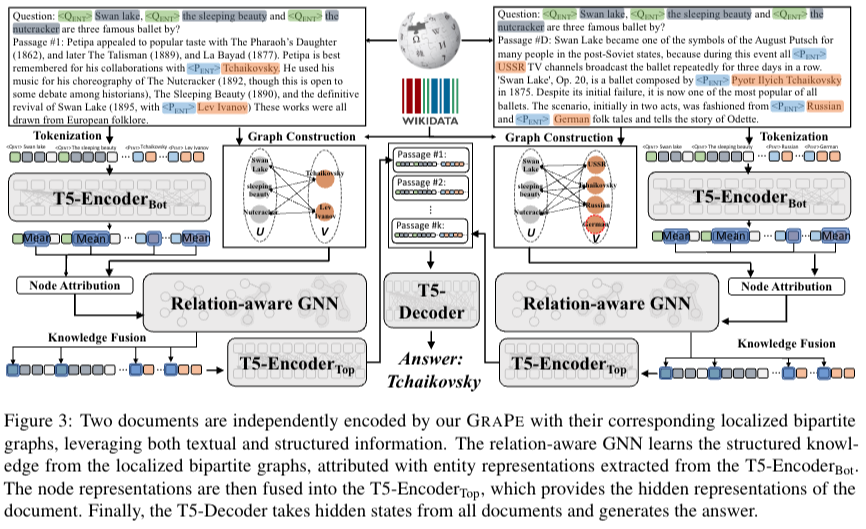
question($q$) 을 바탕으로 k개의 retrieved된 docs($doc_1, doc_2, …, doc_k$)가 있다고 하자. 여기서 $doc_i = \left\{ q^1, q^2, …, q^t, p^1_i, p^2_i, …, p^o_i\right\}$, 이렇게 구성될 때 t는 question 길이, o는 passage token 길이가 된다. $G_i$는 $doc_i$로부터 만들어진 localized bipartite graph가 된다.
$I_s(doc_i), I_e(doc_i), I_t(doc_i)$ 는 각각 start, end, special tokens을 나타내는 indices 이다.
$Enc(.): doc → \mathbb{R}^{(t + 0) \times d}$ 논문의 저자는 encoder를 2부분으로 나눴다. $Enc_{top}(.), Enc_{bot}(.)$각 부분은 만약 layer가 12개라면 L, 12-L 개로 나눠서 사용하였다.
$H_i^b = Enc_{bot}(doc_i)$로 나타낼 수 있다. 그리고 $X_i^G \in \mathbb{R}^{|\mathcal{U} \cup \mathcal{V}|\times d}$ 는 node attributes로 encoder에서 나온 부분에 해당하는 token span을 concat하는 방식으로 만들어진다. 동그라미 플러스 모양은 vertical concatenation을 의미한다.
$X_i^G = \bigoplus avg(H_i^b[StartIdx:EndIdx])^T$, $StartIdx \in I_x(doc_i), EndIdx \in I_e(doc_i)$
구조화된 graph에서 나온 $G_i$와 속성들($X_i^G$)을 GNN 에 넣어주게 된다. GNN에서는 차원을 그래도 유지한다. $H_i^G = GNN(G_i, X_i^G)$, 여기서 $H_i^G$는 학습된 node representation으로 node knowledge를 KG에서 뽑아낸 것이 된다. 여기서 special tokens을 추가해줘서 reader모델로 전달하게 된다. $H_i^u[I_t(doc_i)] = H_i^b[I_t(doc_i)] + H_i^G$ 이렇게 만들어진 것을 $Enc_{top}$을 한번 더 거친 후에 reader모델로 간다, $H_i = Enc_{top}(H_i^G)$,
마지막은 주어진 question q를 바탕으로 k개의 retireved docs를 모두 concat시키고 answer모델로 보내게된다. $answer = Dec(\bigoplus^k_{i=0} H_i)$

다음과같은 복잡한 과정은 4가지로 정리할 수 있다.
1) $Enc_{bot}$를 통해 초기 contextualized representation 얻는 과정
2) node attributes를 fact relation과 fuse시키는 과정(GNN통해서)
3) $Enc_{top}$를 통해 추가적인 information 교환하는과정
4) 마지막으로 decoder를 통한 생성과정

• Relation-aware GNN - 해당 부분은 앞서말한 GNN부분을 설명해주는 부분이다. 전형적인 GNN layer는 $h_v^{(n)} = AGG^{(n)}(\left\{ TRANS^{(n)}(h_u^{(n-1)}): u \in \mathcal{N}(v)\right\})$로 나타낼 수 있따. $\mathcal{N}(v)$는 node v에 대한 neighbors set으로 볼 수 있고, n은 현재 layer index, $h_v^n$는 node v 의 representation, $TRANS$는 이전레이어에서 node representation을 projection시키는 것(message passing을 위함, 새로운 vector space를 만든다.) $AGG$는 통합하는 함수로 node representation을 통합. GRAPE는 multi-layer perceptron을 사용한다($TRANS$를 통해) 이는 $A^{(n)} = \sigma(H^{n-1} \cdot W_t^{(n)} + b_t^{(n)})$으로 나타낼 수 있다. $A^{(n)}$은 intermediate embedding으로 $AGG$로 생각하면된다. $H^{(0)} = X_i^G$로 앞서 언급한 시작부분과 끝부분 span을 encoder통과한 것과 같다($X_i^G = \bigoplus avg(H_i^b[StartIdx:EndIdx])^T$). $W_t^{(n)} \in \mathbb{R}^{d \times d}$, $b_t^{(n)} \in \mathbb{R}^d$는 학습가능한 파라미터들이다. $\sigma$는 activation function이다. 본 논문에서 relation-aware attention mechanism에서도 실험을 진행한다. edge attention weight에 대해 오직 node representation만 고려하는 방식인 GAT와는 다르다. $\begin{aligned} & e_{v, u}^{(n)}=\left(\mathbf{a}v^{(n)} \bigoplus \operatorname{avg}\left(\operatorname{Enc}\left(r{v, u}\right)\right) \bigoplus \mathbf{a}u^{(n)}\right) \cdot \mathbf{W}e^{(n)}, \\ & \alpha_{v, u}=\frac{e{v, u}^{(n)}}{\sum_{m \in \mathcal{N}(v)} e_{v, m}^{(n)}}, \mathbf{h}v^{(n+1)}=\sum{u \in \mathcal{N}(v)} \alpha_{v, u} \cdot \mathbf{a}_v^{(n)}, \end{aligned}$ 위의 수식은 n번째 레이어에서 각 노드v에 대해 노드 representation $h_v^{(n)}$를 나타낸다. $a_v^{(n)}$는 $A^{(n)}$를 통과한 노드 representation이고, $W_e^{(n)} \in \mathcal{R}^{3d \times 1}$은 importance score를 계산한다(node v, u에 대한). 두개의 연결된 노드의 contextualized representation을 얻을 수 있게된다.이 두개의 schema를 multi-head attention pipline을 통해 $H^{(n)} = \sum_{m=0}^M H^{(n,m)}$과정이 진행된다. 좌변은 final node representation으로 GNN()통과한 output을 의미하고, 우변은 m-th, n-th layer의 head를 의미한다. 요약하면 relation-aware GNN은 현재 nodes간의 relationships의 reader’s understanding과 중간 hidden state를 결합한 것이라고 할 수 있다. 이 과정은 encoder 부분에서 facts를 더 잘 이해할 수 있게 한다.