MindMap: Knowledge Graph Prompting Sparks Graph of Thoughts in Large Language Models

Abstract, Introduction

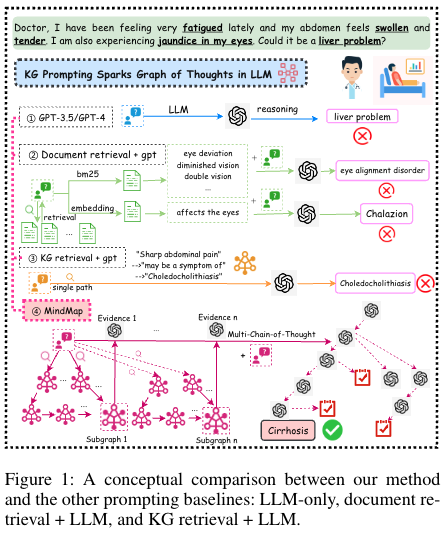
MindMap이라는 prompt + KG(Knowledge Graph)를 바탕으로 GPT3.5를 이용해 QA task에서 GPT4를 이길 수 있다.

LLM의 문제: hallucination(모르는데 아는척 하면서 말하는 현상), Inflexibility(최신 정보 업데이트), Transparency(black box model)
반대로 KG는 Interpretability, flexibility, preciseness 등의 장점이 있어 LLM이 가진 문제를 완화 할 수 있다는 장점이 있다.

KG 를 encoder로 사용해 LLM 과 결합해 학습시키는방법, LLM 학습에 KG triples를 사용하는 방법 등 다양한 학습방법이 존재한다. 본 논문에서는 KG를 이용해 Inference시키는 방식에 MindMap이라는 방식을 제안한다.

기존 방식에서 KG를 이용한 Inference에는 extracted 된 text를 prompt 에 넣어 통합시는 방식이 제안되었다. 해당방식은 그래프적 특징을 무시한다는 단점이 존재한다. 그래프적 구조를 이해시키는 input을 넣으려는 시도도 존재하지만 KG를 기반으로한 여러 evidence 그래프에 걸쳐 복잡한 추론이 필요한 텍스크 생성작업에 거의 시도 되지 않았다.

본 논문의 저자는 plug-and-play prompting approach를 통해 GoT(graph-of-thought 추론능력을 향상시키게 할 수 있다.)방식을 제안했다 해당 방식을 사용하면 3가지 장점이 있다고 소개한다.
1) KG로부터 추출된 사실과 LLM 통합
2) mindmap을 통한 추론으로 최종 답변을 생산
3) KG input으로부터 새로운 패턴 발견

Related Work

이전 연구, 위에서 언급한 방식과 동일하게 Knowledge Graph Augmented LLM에 두 가지 방식이 존재한다. 1) integrating KGs into LLM pre-training, 2) injecting KGs into LLM inference
1) integrating KGs into LLM pre-training 에는 KG entities와 relation을 학습데이터로 통합시키는 방식이 있다.이러한 방식들은 KG knowledge를 directly하게 compression시키는 방식으로 앞에서 언급한 3가지 문제(flexibility, reliability, transparency)를 해결하지 못한다.
2) injecting KGs into LLM inference 에 이전연구로는 fusion KG triples into the inputs of LLM이라는 방식이 존재한다. GNN과 병렬적으로 연결시켜 추론을 진행하도록 adopt 시키거나 text tokens과 KG entities간에 interactions을 LLM layer 중간단계에서 더해주는 방식이 있다. 이러한 최신 연구는 LLM을 fix 시키고 graphical input을 더해주는 방식의 연구 패러다임으로 변화하였다. prompting LLMs for KG entity linking prediction, graph mining, KG question answering 방식들은 LLM이 graph적인 이해를 바탕으로 prediction하는 방식이 진행되었고 이는 KG의 구조성 (KG의 고유한 특징)을 무시한다는 결과가 나온다.

Method - 3 steps

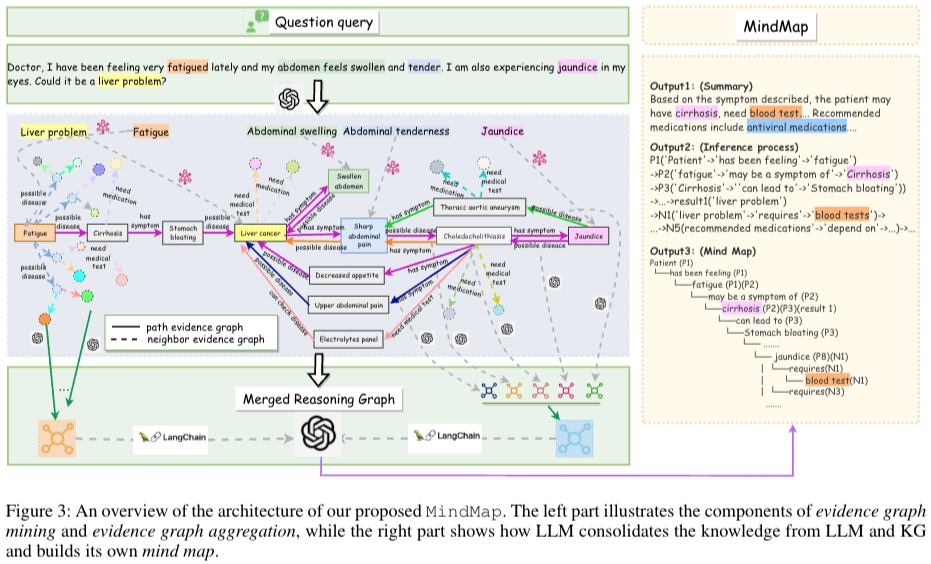
1) Evidence graph mining: raw input과 query source KG($\mathcal{G}$) 로부터 set of entities ($\mathcal{V}_q$)를 identifying 하고 multiple evidence sub-graphs $\mathcal{G_{q}}$ 를 만들기 위한 작업을 진행한다.
2) Evidence graph aggregation: LLM이 retrieved evidence 를 통합하고 이해하기 위해서 sub-graphs의 reasoning graphs $\mathcal{G_{m}}$으로 만든다.
3) LLM reasoning on min map: 마지막으로 reasoning graph와 implicit knowledge를 통합시키고 답변생성하고, 추론과정을 설명하기위한 mind map을 만든다.

Step 1: Evidence Graph Mining

• 외부 KG로부터 relevant evidence sub-graphs $\mathcal{G}_q$만드는 과정
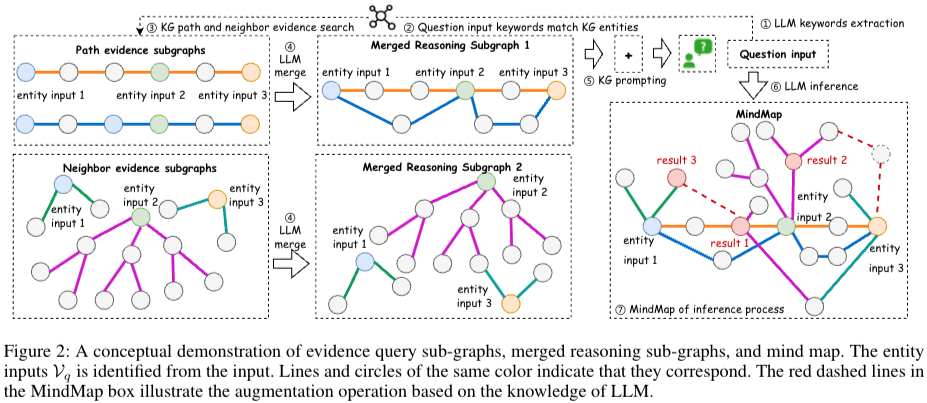
• Entity Recognition: in-context learning사용. Q → LLM → M(생성됨), M → linking → $\mathcal{G}$, $\mathcal{G}$ → encode using bert → $H_{\mathcal{G}}, H_{M}$ $M_k$는 entity set, $Q_k$는 input sentence, exemplars = $\left\{Q_k, M_k\right\}^K_k$, entity set $M$을 추출하기 위해서 entity linking작업을 진행한다. 추출된 M 이 모두 entity set으로 포함되는 것은 아니다. 모든 entity $M$과 $\mathcal{G}$에 엔티티에 대해서 bert를 통한 encoder를 통해 dense embedding($H_{\mathcal{G}}$, $H_{M}$)을 만들었다.
  
• Evidence sub-graphs Exploration Linking작업→ cosine sim을 바탕으로 $M$간의 관계를 연결시켜준다. → $\mathcal{V}_{q}$인 init graph를 만들어준다. source KG → $\mathcal{G} = \left\{<u,r,o> | u \in \psi, r \in \phi, o \in \mathcal{L} \right\}$
  $\mathcal{V}_q$: node set, $\mathcal{E}_q$: edge set, $\psi_{q}$: entity, $\mathcal{L}_q$: textual set, $\phi_q$: relation set
  →sub-graph: $\mathcal{G}^{*} = (\mathcal{V}_q, \mathcal{E}_q, \psi_q, \mathcal{L}_q, \phi_q)$,,,,, $\mathcal{E}_q$에는 each edge $e = <v, v^{\prime}>$, $v, v^{\prime} \in \mathcal{V}_q$.
  source KG에서 sub graph를 만들기 위해 path-based, neighbor-based exploration을 만든다.
  • Path-based Evidence Graph Exploration - fig2 좌측 위 과정 초기 entity set $\mathcal{V}_q$에서 하나의 노드 $\mathcal{V}_q^0$를 선택(= $v_1$, start node). candidate node (=$\mathcal{V}_{cand}$)라고 하자. $v_1$으로부터 k hops개 explore한 후 $v_2$를 잡는다. 단, $v_2 \in \mathcal{V}_{cand}$ 이어야 한다. 그러면 $v_2$를 start node노드로 변경, $\mathcal{V}_{cand}$에서 삭제 후 다음 과정을 똑같이 진행.
    만약 $v_2$에서 k hops를 찾을 수 없다면 해당 segment를 $\mathcal{G}_q^{path}$저장. 그리고 다른 $v_1^{\prime}$을 잡고 반복. 만약 $\mathcal{V}_{cand}$ 가 비었다면, 만들어진 segments를 sub-graphs로 사용
    
  • Neighbor-based Evidence Graph Exploration - fig2 좌측 아래 과정 2개의 과정이 존재함 (a) 각 노드 $v \in \mathcal{V}_q$의 expand by 1-hop to their neighbors → $v^{\prime}$ 에서 add triples $(v, e ,v^{\prime})$ to $\mathcal{G}_q^{nei}$ (b) 모든 $v^{\prime}$으로부터 question과 semantically 관련있는지확인. 만약 관련있다면 1-hop neighbors of $v^{\prime}$ 한번 더 확장 → $(v_{nei}, e^{\prime}, v^{\prime})$ to $\mathcal{G}_q^{nei}$
  이렇게 $\mathcal{V}_q$를 업데이트 시킨다. 모든 탐험 이후에 $\mathcal{G}_q^{path}$, $\mathcal{G}_q^{nei}$ pruning 과정을 통해 줄여준다. (너무 많은 정보량은 overhead를 만들 수 있다. 하지만 diversity는 유지하는 방식으로) (a) cluster all sub-graphs by their head entities. 각 엔티티들은 raw query and filled in $\mathcal{V}_q$에 있었던 것들이다. (b) check each cluster and randomly sample $k$ if the number of graphs exceed the pre-defrined threshold

Step 2: Evidence Graph Aggregation

최종 output을 만들기위해 merge 과정을 진행
evidence route set 을 만들기위해 LLM에 instruction prompt를 준다(각 evidence sub graph구조를 묘사하게 하는 과정). sub-graph $\mathcal{G}^*_{q}$에서 evidence route set $C_q = \left\{ c_q^{(1)}, …, c_q^{(n)} \right\}$이다. 각 $c_q^{(*)}$는 pathway를 나타낸다. 저자는 모든 path-based sub-graphs($\mathcal{G}_q^{path}$)와 neighbor-based sub-graph($\mathcal{G}_q^{nei}$)에 대해서 각각 prompting을 수행함. → $\mathcal{G}_m = \left\{ \mathcal{G}_q^{path}, \mathcal{G}_q^{nei}\right\}$ reasoning graph 생산.
이 과정은 두가지의 장점이 있다. 1) LLM이 작은 sub-graph전체를 볼 수 있게 한다. 2) LLM은 비슷한 entities들에 대한 모호성 해결을 돕는다.

Step3: Inference with LLM and KG knowledge

해당 스텝에서는 최종 output을 만들기위해 만들어진 2개의 $\mathcal{G}_q^{path}, \mathcal{G}_q^{nei}$을 통합하는 과정이 진행된다.
Prompting for Graph Reasoning

5개의 components를 통해 프롬프트 구성(system instruction, question, evidence graphs($\mathcal{G}_m$) graph-of-thought instruction, exemplars). GoT의 과정은 llm에게 think step by step을 넣어준다. Fig3에 오른쪽 박스가 마인드맵 형식이 된다.