ABSTRACT
최근 수학 도메인에서 언어모델을 활용한 성능이 매우 좋게 나오고 있다. 본 논문에서는 task와 methodologies를 중점적으로 mathematical LMs 에 대해서 설명한다. 특히 instruction learning, tool-based methods, fundamental CoT techniques, and advanced CoT methodologies 부분을 중점적으로 소개한다. 또한 benchmark dataset과 augmented datasets에 대해 소개한다.
INTRODUCTION

mathematical calculation: arithmetic representation and arithmetic calculation.
mathematical reasoning: problem-solving and theorem proving.
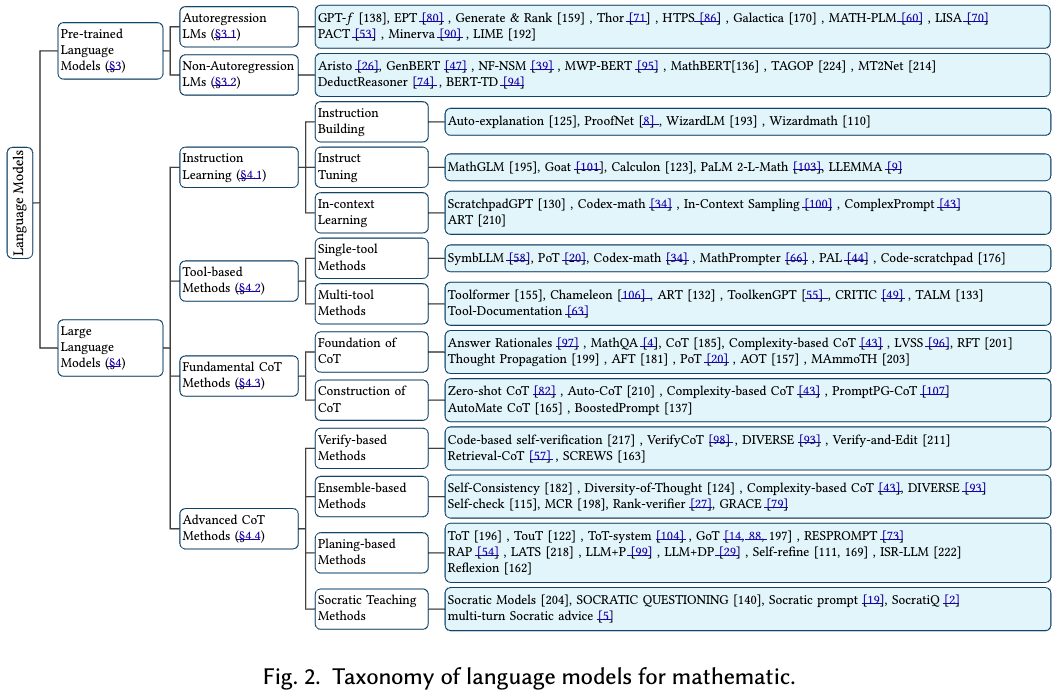
- PLMs-based approaches
including autoregression
non-autoregression LMs
LLMs-based methodologies which include instruction learning
tool-based strategies
fundamental CoT techniques
advanced CoT methodologies (§4.4)
본 논문에서는 또한 60여개의 mathematical datasets을 소개한다.
2. MATHEMATICAL TASKS
본 section에서는 수학 테스크 (calculation and reasoning)에 대해 요약을 진행함
Mathematical calculation
Arithmetic Representation: bert와 같은 embedding 모델을 이용해서 representation을 뽑아내는 과정. genBERT와 같은 모델이 존재한다.
Arithmetic Calculation: LLM을 이용해서 계산하는 것. 전통적으로 LLM 은 8자리 이상의 복잡한 곱셈연산을 못한다고 가정했었다. 그러나 최신 접근방법중 scratchpadGPT는 CoT를 중간중간에 계속 생성하게 해서 8자리 곱셈연산을 가능하게 했다. Goat 논문은 fine-tuning을 이용해 llama 모델이 gpt4 보다 산술 연산을 더 잘하게 만들었으며, Math-GLM 논문은 calculator 없이 gpt가 수학문제를 풀 수 있다고 주장했다 (산술 테스크를 decompose complex arithmetic expressions into simpler steps) 해당 과정을 통해서 점진적으로 답변생성과 computation rule을 학습할 수 있었다고 주장.
Mathematical reasoning
Math Problem Solving: AI에서 수학문제 영역은 algorithms, computational models, LLM to understand 등이 사용된다. 이런 approach는 advanced mathematics (algebra, geometry, statistics and calculus)를 해결할 수 있는 방법들이다. 해당 분야는 Math Word Problems (MWPs) 와 Math Question Answering (MQA) 로 나뉜다.
Math Word Problems (MWPs): description 형태를 바탕으로 수학 문제를 해결하는 것을 의미한다. MathPrompter 에서는 LLM call을 이용해서 복잡한 reasoning을 통해 사람과 같이 이해를 하고 문제를 해결한다. SCALING RELATIONSHIP 논문은 pre-training loss가 performance metric 이 될 수 있으며, Rejection sampling Fine-Tuning (RFT)를 이용해 supervised models to generate and collect correct reasoning paths 통해서 더 좋은 inference generalization and improvement할 수 있었다. MetaMath 논문은 데이터셋 제시. WizardMath 논문은 mathematical reasoning 능력을 향상시키기 위해서 reinforcing 방식 (autonomous self improvement)을 사용했다. MathAttack 논문은 adversarial input을 만들어서 test their mathematical problem-solving abilities. LLEMMA 라는 논문은 Proof-Pile-2 라는 데이터셋을 만들어 continue pretraining을 진행했다.
Math Question Answerings (MQA): MQA는 computational task를 의미한다. 자동적으로 자연어로된 수학과 관련된 question을 해결하는 작업이다. 해당 테스크는 정확한 text 이해와 이를 적절한 수학적 representation으로 변환시켜주는 작업이 challenge이다. 이는 사람의 problem-solving 과정을 묘사한 것이기도 하다.
Theorem proving (TP): TP는 demonstrating 이 올바른지 확인하는 작업이다. 해당 작업은 사람이 증명한 데이터를 사용해 테스크를 진행한다.
LLMS-BASED METHODS
Instruction Learning
Instruction Building: semi-supervised approach. WizardLM은 Evol-Instruct로 자동적으로 high-quality instructions 를 llm 스스로 생성하게 했다. 또한 Wizardmath는 reinforced Evol-instruct method (RLEIF)를 제안하면서 더 복잡한 instruct dataset을 만들었다.
Instruction Tuning: pre-train에 비해 적은데이터로학습 가능 및 human intent 반영. PaLM 2-L-Math 논문은 3가지 fine-tuning 전략을 제안했다. 첫 번째로 step-by-step solution (SSFT)을 학습시키는 것이고, 두 번째로 select best solution from a set of potential solutions (Solution-Cluster Re-ranking=SCR) 를 제안했다. 마지막으로 SSFT 와 SCR을 합쳐 학습과 평가를 동시에 할 수 있는 방법을 제안했다.
In-context Learning: ScratchpadGPT 방식은 생성중간에 cot 과정을 진행시키는 방법 이고 codex-math 논문은 코드를 통해 program을 생성시켜 few-shot에 통합시켜 (automatically) 성능을 증가시켰다.
Tool-based Methods
LLM은 tool을 사용할 수 있게 designed 되었다. (code, calculators for their problem solving.)
Single-tool Methods: reasoning 능력을 증가시키기위해 math-specific tool을 이용하거나 programs 을 LLM 에 사용하는 방법. PoT 방식은 CoT와 python 코드등의 프로그램을 이용해 university level까지 도달할 수 있었다.
Multi-tool Methods: LLM과 다양한 tools 사용가능하게하는 방법이다. chameleon 이라는 논문은 llm, git, image, code, search 등 다양한 tool을 통합한 방식을 제안했다. Automatic Reasoning and Tool-use (ART) framwork는 program으로 intermediate reasoning을 생성하게 했다. CRITIC 이라는 논문은 tool을 활용한 self verification을 진행하였다. Tool Augmented Language Model (TALM)은 여러개의 tool을 bootstrapping 하여 성능을 올렸다.
Fundamental CoT Methods
Foundation of CoT:
CoT는 rationale 생성을 통해 더 정확한 answer을 뽑아내는 과정이다. LVSS는 스텝별 검증을 진행하는 것으로 학습단계에서 올바른 supervision method를 고르는 것이 중요하다고 주장한다. Tought Propagation은 유사한 problem을 모아서 현재 문제를 해결하는 방법을 제안한다. Mammoth 논문은 hybride instruction tuning (integrate CoT and PoT) 방식을 제안한다.
Construction of CoT:
Complexity-based prompting 논문은 CoT에서 발전된 결과로 CoT chain이 많이 가져갈 수록 성능이 좋아지며, 일정 rationales 갯수를 가진 것들로 voting을 진행해 답변을 구하면 성능이 좋아진다고 주장함. PromptPG-CoT 논문은 policy gradient를 이용해 적절할 CoT demonstrations를 고르도록 모델을 학습시킴. AutoMate CoT는 위와 비슷하며 variance를 낮춘 것. BoostedPrompt는 방법론들을 ensemble 시킨것.
Advanced CoT Methods (p13)
Verify-based Methods: LLM은 부정확한 reasoning steps를 생성하기도 하고 이는 틀린 정답 생성에 큰 영향을 미친다. 해당 에러를 줄이는 feedback을 주는 방식이 존재한다. (스텝별 voting 진행, decompose a reasoning = a series of step-by-step subprocesses, ) code-base verify, verify and edit (retrieval tool 사용), summarize 를 이용한 verify
Ensemble-based Method: voting이나 ranking을 바탕으로 불확실한 reasoning process를 줄이려는 시도들이 많다. Self-Consistency, Diversity of Thought 방식은 aggregates the responses via majority voting을 이용한 방식이다. Complexity-based CoT 는 복잡한 reasoning path 에서 답변을 추출하는 방식. DIVERSE 논문은 weighted voting 을 이용해 부정확한 답변을 필터링한다. 하지만 voting 방식은 overlook 하는 경향이 있다. Ranking 방식에는 Rank-verifier은 verifier를 이용해 가장 높은 rank를 사용하는 방식이다.
Planning-based Methods: CoT의 구조는 sequential 이다. planning-base 방식은 refinement와 reflection을 통해 reasoning step을 만들어간다. ToT는 tree 구조의 reasoning path 를 제안했다. 각 노드는 reasoning step이고 edge는 node간의 dependencies 이다. ToT는 self-assessment를 진행한다. (ToT의 확장 버전: TouT and multi-module ToT). GoT는 Graph of Thought로 ToT와 비슷하다. RESPROMPT는 residual connection prompting으로 input을 복잡한 Reasoning graphs로 변환시킨 후 진행한다. RAP 는 MCTS를 이용한 reasoning 방식이다.
Socratic Teaching Methods(p15): 대화를 통해 대화 상대방에게 스스로 답을 찾도록 돕는 방식.
CHALLENGES AND FUTURE DIRECTIONS
Faithfulness
hallucination and faithfulness 줄이는 문제가 중요하다. 이를 해결하기위해 RLHF, extra knowledge integrating, tool 을 이용한 방식이 사용된다.
Multi-modal
diagrams, graphs, mathematical symbol 의 information 단순 text로서 사용하는게 아니라 다른 형태 그 자체로 사용할 수 있다.
Uncertainty
uncertainty of LLM 은 ambiguity와 variability problem을 초래할 수 있다. (확률을 기반한 모델이기 때문에) 이러한 문제를 피해 정답으로 잘 navigate할 수 있는 방법이 필요하다.
Evaluation
LM을 이용해 수학을 robust하게 평가하는것은 남아있는 challenge이다. 모델의 성능을 정확하게 평가할 수 있는metric이 필요하다.. 또한 reasoning, theorem probing 도 해당된다.
