Fuzzy Logic

인화·2025년 10월 18일

인공지능

목록 보기

5/6

1. 퍼지논리

1.1 퍼지 논리(Fuzzy Logic)란

Fuzzy라는 단어는, 흐릿한, 불분명한이라는 의미를 가진다. 여기서도 알 수 있듯, 퍼지 논리(Fuzzy Logic)는 명확하게 구분되지 않는 개념을 수학적으로 다루는 방법, 다시 말해 정확하지 않거나(imprecise) 불완전한(incomplete) 정보를 처리하는 데 유용한 논리 체계를 의미한다. 이는 1965년 L. A. Zadeh가 퍼지 집합 이론을 제시하면서 등장했고, 이후 퍼지 명제나 규칙을 다루기 위한 퍼지 논리로 발전하였다.

1.2 크리스프 집합 vs 퍼지 집합

크리스프 집합 (Crisp Set) : 원소가 집합에 속하면 1, 아니면 0
퍼지 집합 (Fuzzy Set) : 원소가 집합에 속하는 정도를 0~1 사이 값으로 표현
$키 큰 사람 = {(170, 0.3), (175, 0.5), (180, 0.95), (190, 1.0)}$
명제 논리 == 기존 집합 (크리스프 집합), 퍼지 논리 == 퍼지 집합

원소가 속하거나 속하지 않는 두 가지로만 구분되는 크리스프 집합과는 달리, 퍼지 집합에서는 원소가 특정 집합에 속하는 정도를 표현함.
그렇다고 해서, 퍼지 논리가 애매한 논리인 것은 아니다. 퍼지 논리는 애매함을 다루는 질서정연한 논리이다.

1.3 퍼지 연산자

교집합 (AND) : $min(μ_A(x), μ_B(x))$
합집합 (OR) : $max(μ_A(x), μ_B(x))$
여집합 (NOT) : $1 - μ_A(x)$

1.4 퍼지 추론 과정

퍼지화 (Fuzzification) : 입력값을 소속 함수로 변환
규칙 적용 (Rule Application) : 각 규칙의 조건에 맞게 소속 함수 값을 계산
결합 (Aggregation) : 여러 규칙의 결과를 결합
역퍼지화(Defuzzification) : 퍼지 결과를 실제 수치로 변환

1.4.1 헤지

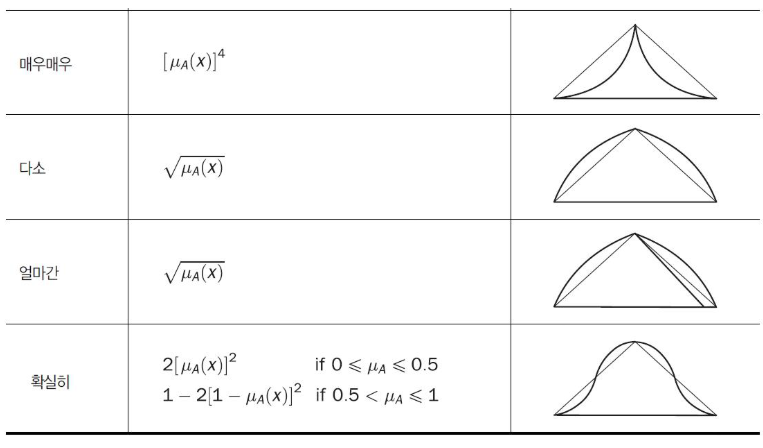
퍼지 집합의 모양을 바꾸는 퍼지 집합 한정사 (퍼지 집합의 의미를 강화하거나 약화시키는 연산자처럼 작동)
(ex) 매우, 얼마간, 꽤, 다소, 조금 등

1.4.2 퍼지 규칙

IF x가 A THEN y는 B에서 x, y는 언어 변수, A, B는 각각 논의 영역 X와 Y의 퍼지 집합에서 결정된 언어 값
규칙 후건의 출력 값이나 소속도는 전건의 소속도에서 직접 추정할 수 있음.
퍼지 규칙의 전건은 여러 개일 수 있으며, 전건의 모든 부분은 동시에 계산되고, 숫자 하나로 결정됨. (-> 이를 위해 퍼지 집합 연산을 사용함)
후건 역시 여러 개일 수 있음. (ex) IF 기온이 높다 THEN 뜨거운 물은 줄어든다 시원한 물은 늘어난다

1.4.3 퍼지 추론 기법

맘다니형 추론 : 가장 흔히 쓰이는 퍼지 추론 기법

1단계 : 입력 변수의 퍼지화
2단계 : 규칙 평가
3단계 : 출력으로 나온 규칙의 통합
4단계 : 역퍼지화

맘다니형 추론 예시 - 입력 2개, 출력 1개, 규칙 3개 문제 예시

x, y, z는 언어 변수 (프로젝트 자금, 인력, 위험도)
A1, A2, A3는 논의 영역 x 상의 퍼지 집합에서 정해지는 언어 값 (부족하다, 한계 수익점에 있다, 충분하다)
B1, B2는 논의 영역 y 상의 퍼지 집합에서 정해지는 언어 값 (적다, 많다)
C1, C2, C3는 논의 영역 z 상의 퍼지 집합에서 정해지는 언어 값 (낮다, 중간이다, 높다)

1단계 : 입력 변수의 퍼지화

크리스프 입력 x1(프로젝트 자금), y1(프로젝트 인력)을 받고, 이를 적합한 퍼지 집합에 각각 어느 정도로 속할지 결정
논의 영역 : X, Y

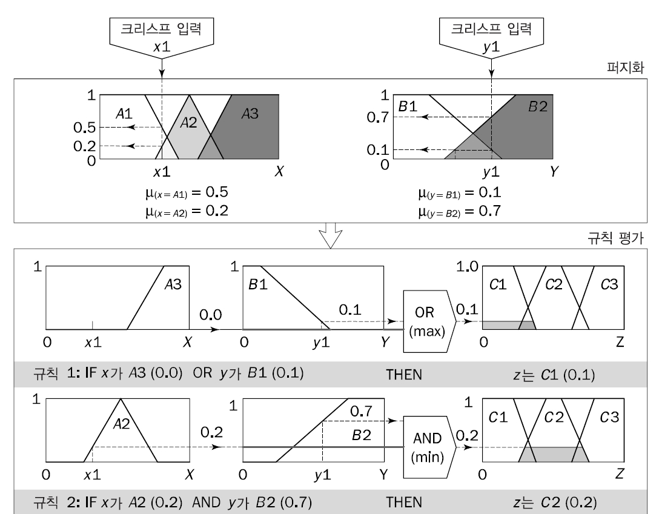
2단계 : 규칙 평가

퍼지 입력 $μ_{(x=A1)} = 0.5$ , $μ_{(x=A2)} = 0.2$ , $μ_{(x=B1)} = 0.1$ , $μ_{(x=B2)} = 0.7$ 을 받아 퍼지 규칙의 전건에 적용
주어진 퍼지 규칙에 전건이 여러 개 있다면 퍼지 연산자를 사용해 전건의 평가 결과를 나타내는 숫자 하나를 얻고, 이 숫자를 후건의 소속 함수에 적용함.

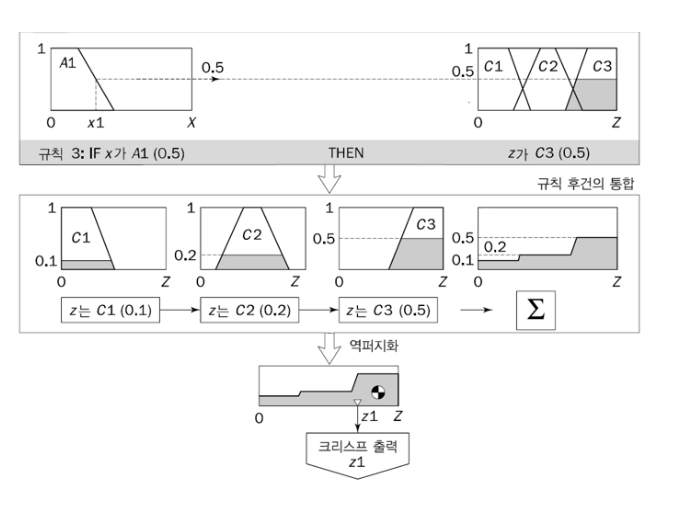
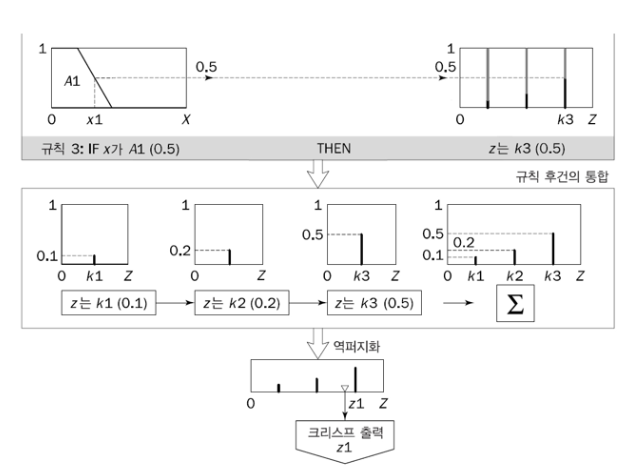
3단계 : 출력으로 나온 규칙의 통합

여러 개 규칙이 동시에 발화되면 각 규칙마다 후건부 퍼지 집합이 나오는데, 이 결과들을 하나의 최종 퍼지 집합으로 합치는 것

4단계 : 역퍼지화

최종 퍼지 집합을 단일 수치로 바꾸는 것
대표적인 방법 -> 무게 중심법

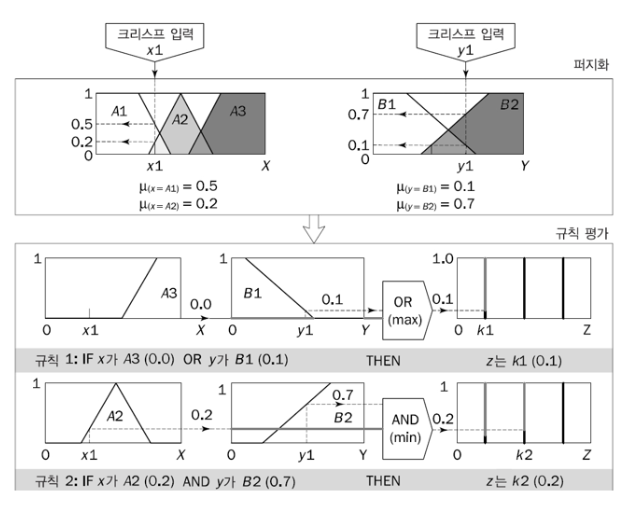
스게노형 추론 : 퍼지 집합 대신 입력 변수에 대한 수학 함수를 사용하는 추론 방법

맘다니형과 거의 비슷하나, 후건부가 입력 변수에 대한 수학 함수라는 차이가 존재함.
낮다, 보통이다 등의 언어적 표현이 아닌 상수로 값을 표현함.
(ex) IF 온도가 높음 THEN 팬 속도 = 0.5 * 온도 + 20
규칙 후건부를 단일체로 표현할 수 있음. (규칙 후건을 통합할 때 연속적인 것이 아닌 개별적인 값들로써 역퍼지화가 가능함. / 다시 말해 단일체의 가중평균으로 출력을 구함.)
효율적인 계산 / 빠른 역퍼지화

스게노형 퍼지 규칙 형식
IF x가 A
AND y가 B
THEN Z는 f(x, y)
// x, y, z : 언어 변수
// A, B : 논의 영역을 x, y로 하는 퍼지 집합
// f(x, y) : 수학 함수

맘다니형 추론과 스게노형 추론의 차이

맘다니형 추론 방법은 전문 지식을 더욱 객관적이고 인간의 방식으로 설명할 수 있다는 장점이 있으나, 퍼지 집합을 다루기에 계산 비용이 많이 듦.
스게노형 추론 방법은 계산을 효율적으로 할 수 있고, 최적화나 적응형 기법과 함께 잘 작동함.

1.5 함축 연산자 처리

IF-THEN 부분을 연결하는 방법으로, IF 부분의 소속도 값과 THEN 부분의 소속도 값을 이용해 출력을 결정한다.
(ex) IF (0.7) THEN (aircon is "high") -> min(0.7, "high")

Code Example

팬 속도 제어

입력 : 온도 (0~40℃)
출력 : 팬 속도 (0~100%)
규칙 예시 :
- IF 온도가 낮음 → 팬 속도 낮음
- IF 온도가 보통 → 팬 속도 보통
- IF 온도가 높음 → 팬 속도 높음

!pip install scikit-fuzzy matplotlib --quiet

import numpy as np
import skfuzzy as fuzz
import matplotlib.pyplot as plt

# -----------------------------------------------------
# 1. 변수 정의
# -----------------------------------------------------
x_temp = np.arange(0, 41, 1) # 0부터 40까지 숫자 배열 (온도)
x_fan = np.arange(0, 101, 1) # 0부터 100까지 숫자 배열 (팬 속도)

# -----------------------------------------------------
# 2. 소속 함수 정의 (Membership function를 정의)
# -----------------------------------------------------
# fuzz.trimf : Triangular membership function
# syntax : y = trimf(x,params)
# (입력값, [삼각형 소속 함수 세 꼭짓점 좌표])
# (왼쪽 시작점, 꼭짓점(최대 소속도=1), 오른쪽 끝점)
temp_low = fuzz.trimf(x_temp, [0, 0, 20])
temp_med = fuzz.trimf(x_temp, [10, 20, 30])
temp_high = fuzz.trimf(x_temp, [20, 40, 40])

fan_low = fuzz.trimf(x_fan, [0, 0, 50])
fan_med = fuzz.trimf(x_fan, [20, 50, 75])
fan_high = fuzz.trimf(x_fan, [50, 100, 100])

# -----------------------------------------------------
# 3. 입력값 설정
# -----------------------------------------------------
# fuzz.interp_membership(x, xmf, xx) : 특정 입력값에 대한 소속도(멤버십 값) 계산
# x : 입력 범위, xmf : 퍼지 집합의 멤버십 함수, xx : 평가 원하는 값
temp_value = 28

temp_level_low = fuzz.interp_membership(x_temp, temp_low, temp_value) # 범위밖 -> 소속도 : 0
temp_level_med = fuzz.interp_membership(x_temp, temp_med, temp_value) # (c - x) / (c - b) -> (30 - 28) / (30 - 20) -> 소속도 : 0.2
temp_level_high = fuzz.interp_membership(x_temp, temp_high, temp_value) # (x - a) / (b - a) -> (28 - 20) / (40 - 20) -> 소속도 : 0.4

print("소속도(28도) : 낮음 = %.2f, 보통 = %.2f, 높음 = %.2f" % (temp_level_low, temp_level_med, temp_level_high))

# -----------------------------------------------------
# 4. 규칙 적용
# -----------------------------------------------------
fan_activation_low = np.fmin(temp_level_low, fan_low) # IF 온도가 낮음 → 팬 속도 낮음
fan_activation_med = np.fmin(temp_level_med, fan_med) # IF 온도가 보통 → 팬 속도 보통
fan_activation_high = np.fmin(temp_level_high, fan_high) # IF 온도가 높음 → 팬 속도 높음

# -----------------------------------------------------
# 5. 결과 결합 및 역퍼지화
# -----------------------------------------------------
# np.fmax(a, b) : 두 값 중 큰 값 반환 (OR 연산)
# aggregated : 소속도가 가장 큰 값 찾는 거
aggregated = np.fmax(fan_activation_low, np.fmax(fan_activation_med, fan_activation_high))
# fuzz.defuzz(x, mf, 'centroid') : 퍼지값을 실제 값으로 반환
# 'centroid' : 집합의 평균 계산
# 'bisector' : 곡선을 반으로 나눈 값
# 'mom/som/lom' : 최대 소속도를 갖는 값들 중 각각 중앙/최소/최대값
print(aggregated)
fan_result = fuzz.defuzz(x_fan, aggregated, 'centroid')
print("결정된 팬 속도 : %.2f %%" % fan_result)

numerator = np.sum(x_fan * aggregated)
denominator = np.sum(aggregated)
fan_result = numerator / denominator
print(numerator, denominator, fan_result)

# -----------------------------------------------------
# 6. 시각화
# -----------------------------------------------------
plt.figure(figsize = (8, 4))
plt.plot(x_fan, fan_low, 'b', linewidth=1.5, label='Low')
plt.plot(x_fan, fan_med, 'g', linewidth=1.5, label='Medium')
plt.plot(x_fan, fan_high, 'r', linewidth=1.5, label='High')
plt.axvline(fan_result, color='k', linestyle='--', label="Output (defuzzified)")
plt.legend()
plt.title("Fuzzy Inference Result (Fan Speed)")
plt.show()

팁 주기 문제

입력 : 서비스 (0-10), 음식 맛 (0-10)
출력 : 팁 퍼센트 (0-30%)
규칙 예시 :
- IF 서비스가 형편없다 OR 음식이 맛없다 → 팁 적게
- IF 서비스가 보통이다 → 팁 보통
- IF 서비스가 훌륭하다 OR 음식이 맛있다 → 팁 많이

# -----------------------------------------------------
# 1. 변수 정의
# -----------------------------------------------------
x_service = np.arange(0, 11, 1) # 0부터 10까지 숫자 배열 (서비스)
x_food = np.arange(0, 11, 1) # 0부터 10까지 숫자 배열 (음식 맛)
x_tip = np.arange(0, 31, 1) # 0부터 30까지 숫자 배열 (팁 퍼센트)

# -----------------------------------------------------
# 2. 소속 함수 정의
# -----------------------------------------------------
# fuzz.trimf : Triangular membership function
# (입력값, [삼각형 소속 함수 세 꼭짓점 좌표])

# 서비스 : 0 ~ 10
service_low = fuzz.trimf(x_service, [0, 0, 5])
service_med = fuzz.trimf(x_service, [0, 5, 10])
service_high = fuzz.trimf(x_service, [5, 10, 10])

# 음식 맛 : 0 ~ 10
food_bad = fuzz.trimf(x_food, [0, 0, 5])
food_ok = fuzz.trimf(x_food, [0, 5, 10])
food_good = fuzz.trimf(x_food, [5, 10, 10])

# 팁 : 0 ~ 30
tip_low = fuzz.trimf(x_tip, [0, 0, 15])
tip_med = fuzz.trimf(x_tip, [0, 15, 20])
tip_high = fuzz.trimf(x_tip, [15, 30, 30])

# -----------------------------------------------------
# 3. 입력값 (서비스 = 7, 음식 = 8)
# -----------------------------------------------------
# fuzz.interp_membership(x, xmf, xx) : 특정 입력값에 대한 소속도(멤버십 값) 계산
# x : 입력 범위, xmf : 퍼지 집합의 멤버십 함수, xx : 평가 원하는 값

service_val = 7
food_val = 8


service_level_low = fuzz.interp_membership(x_service, service_low, service_val) # 범위 밖
service_level_med = fuzz.interp_membership(x_service, service_med, service_val) # 높음
service_level_high = fuzz.interp_membership(x_service, service_high, service_val) # 높음

print("소속도(서비스 = 7) : 낮음 = %.2f, 높음 = %.2f, 높음 = %.2f" % (service_level_low, service_level_med, service_level_high))


food_level_bad = fuzz.interp_membership(x_food, food_bad, food_val) # 범위 밖
food_level_ok = fuzz.interp_membership(x_food, food_ok, food_val) # 높음
food_level_good = fuzz.interp_membership(x_food, food_good, food_val) # 높음

print("소속도(음식 = 8) : 낮음 = %.2f, 높음 = %.2f, 높음 = %.2f" % (food_level_bad, food_level_ok, food_level_good))

# -----------------------------------------------------
# 4. 규칙 적용
# -----------------------------------------------------
rule1 = np.fmax(service_level_low, food_level_bad) # 서비스가 나쁘거나 음식이 별로면
activation_rule1 = np.fmin(rule1, tip_low) # 팁 조금

rule2 = service_level_med # 서비스 중간
activation_rule2 = np.fmin(rule2, tip_med) # 팁 중간

rule3 = np.fmax(service_level_high, food_level_good) # 서비스도 좋고 음식도 좋음
activation_rule3 = np.fmin(rule3, tip_high) # 팁 많이


# -----------------------------------------------------
# 5. 결과 결합 및 역퍼지화
# -----------------------------------------------------
aggregate = np.fmax(activation_rule1, np.fmax(activation_rule1, activation_rule2))
print(aggregate)
tip_result = fuzz.defuzz(x_tip, aggregate, 'centroid')
print("결정된 팁 : %.2f %%" % tip_result)

numerator = np.sum(x_tip * aggregate)
denominator = np.sum(aggregate)
fan_result = numerator / denominator
print(numerator, denominator, fan_result)

# -----------------------------------------------------
# 6. 시각화
# -----------------------------------------------------
plt.figure(figsize = (8, 4))
plt.plot(x_tip, tip_low, 'b', linewidth=1.5, label='Low')
plt.plot(x_tip, tip_med, 'g', linewidth=1.5, label='Medium')
plt.plot(x_tip, tip_high, 'r', linewidth=1.5, label='High')
plt.axvline(tip_result, color='k', linestyle='--', label="Output (defuzzified)")
plt.legend()
plt.title("Fuzzy Inference Result (Tip Percentage)")
plt.show()