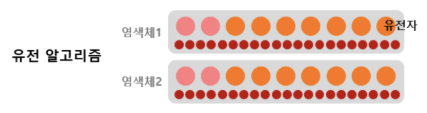
유전자 알고리즘 (Genetic Algorithm)
유전자 알고리즘이란, 인간의 유전 현상을 모델링하는 알고리즘으로, 자연 진화 과정을 모방하여 모델링하고, 최적해를 찾는다.
이때, 각 세대마다 선택(selection), 교차(crossover), 돌연변이(mutation) 과정을 거치며 더 나은 해를 찾아가며, 이 과정에서 전역 최적점을 찾을 수 있고, 적합도 평가에 기울기 정보를 필요로 하지 않으므로 함수의 연속이나 미분가능성 등의 제약을 받지 않는다는 장점이 존재한다.
염색체와 유전자
염색체 (chromosome)(=individual)는 여러 개의 유전자 (gene)로 구성되며, 각 유전자는 문제 공간의 한 부분이다. 전체 염색체는 문제 공간을 염색체 공간으로 인코딩한 것을 의미한다.
세대 (generation)는 여러 개의 염색체로 구성된 하나의 집합을 의미한다.
평가 함수와 적합도
유전자 알고리즘의 평가 함수(Evaluation function)는 현재의 염색체가 얼마나 문제를 잘 해결하고 있는지를 나타내는 적합도(Fitness)를 반환한다.
유전자 알고리즘에서 적합도는 염색체의 성능을 나타내며, 높은 적합도(최적해에 가까운 것)를 가지는 염색체가 다음 세대에 더 많이 전달된다.
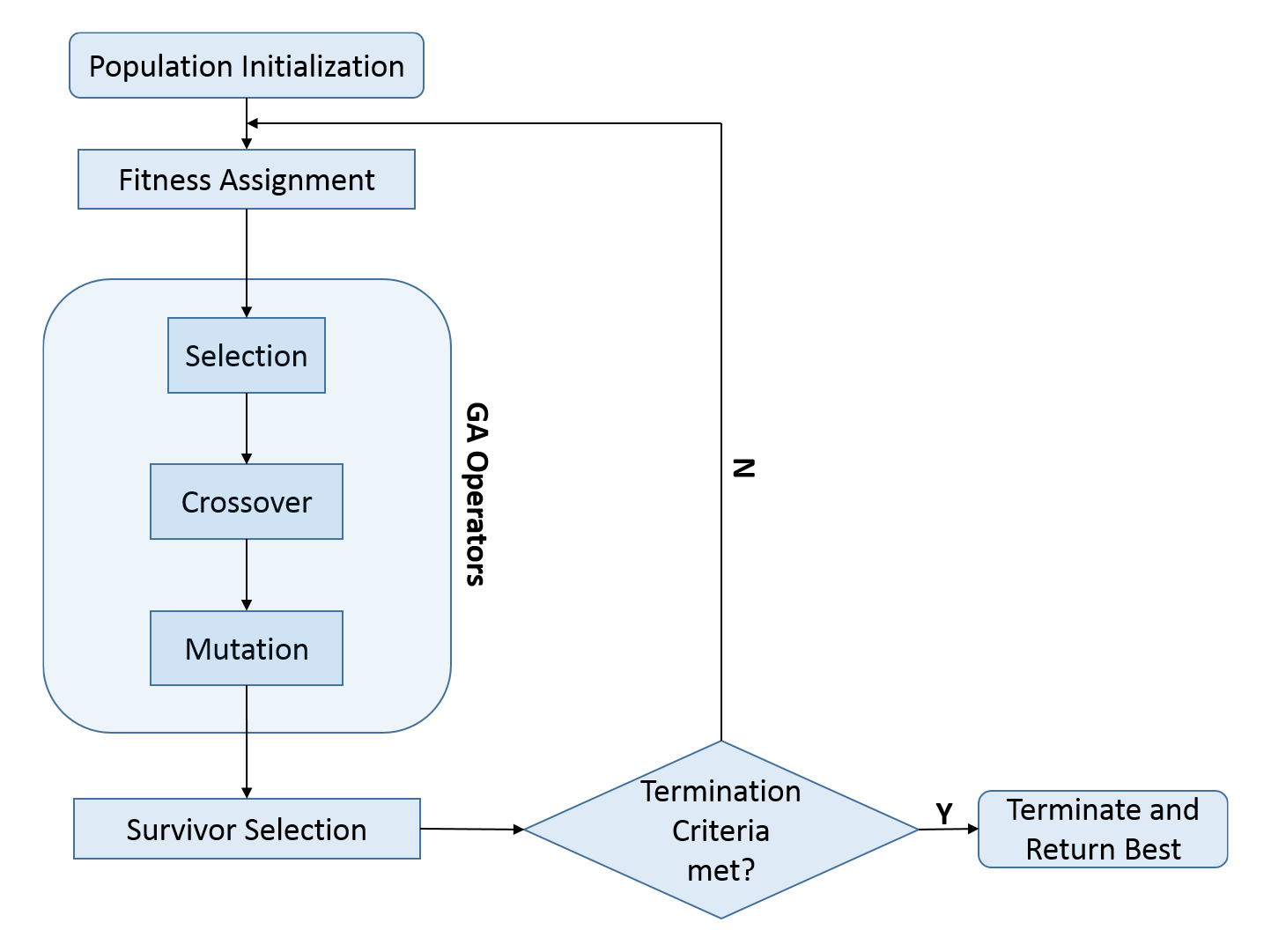
유전자 알고리즘의 절차
- Initialization : 초기 집단(population)을 랜덤하게 생성하는 단계
- Selection : 현재 집단에서 적합도가 높은 개체를 선택해 다음 세대에 전달하는 과정
- Crossover : 선택된 두 부모 염색체를 결합하여 새로운 염색체(자식 염색체)를 생성하는 단계
- Mutation : 일정 확률로 유전자 값을 무작위로 변경하는 단계
- Evaluation : 새로운 집단의 적합도를 평가하는 단계
- Check the termination conditions : 종료 조건을 확인하는 단계
선택 연산자
- Rootlet Wheel Selection : 각 개체가 선택될 확률이 그 개체의 적합도에 비례함.
- 평가 함수를 통해 염색체의 적합도를 계산한 뒤, 적합도에 비례해 룰렛 휠에 염색체를 배당하여 적합도가 높은 염색체가 더 많이 선택될 수 있도록 하는 것
- 적합도 크기에 따라 비율이 결정됨.
- Rank-based Selection : 개체들의 적합도에 따라 랭크를 매겨서 상위 개체들을 선택함.
- 상위 개체들만 계속 선택되므로 룰렛 휠이나 토너먼트 방식에 비해 다양성이 적음.
- Tournamant Selection : 일정 수의 개체를 선택하고 토너먼트를 진행해 적합도가 높은 것을 선택함.
- 무작위로 k개 개체를 선택하고, 이 중 적합도가 가장 높은 개체를 다음 세대로 선택함.
- 이 과정을 반복해 새로운 population을 구성함.
교차 연산자
선택된 부모 개체(염색체)로부터 자손(offspring)을 생성하는 과정을 의미한다.
- multipoint CX : 부모 염색체를 여러 지점에서 나눠 교환하는 방법으로, 교차점이 1개면 1-point crossover, 2개면 2-point crossover와 같이 표현함.
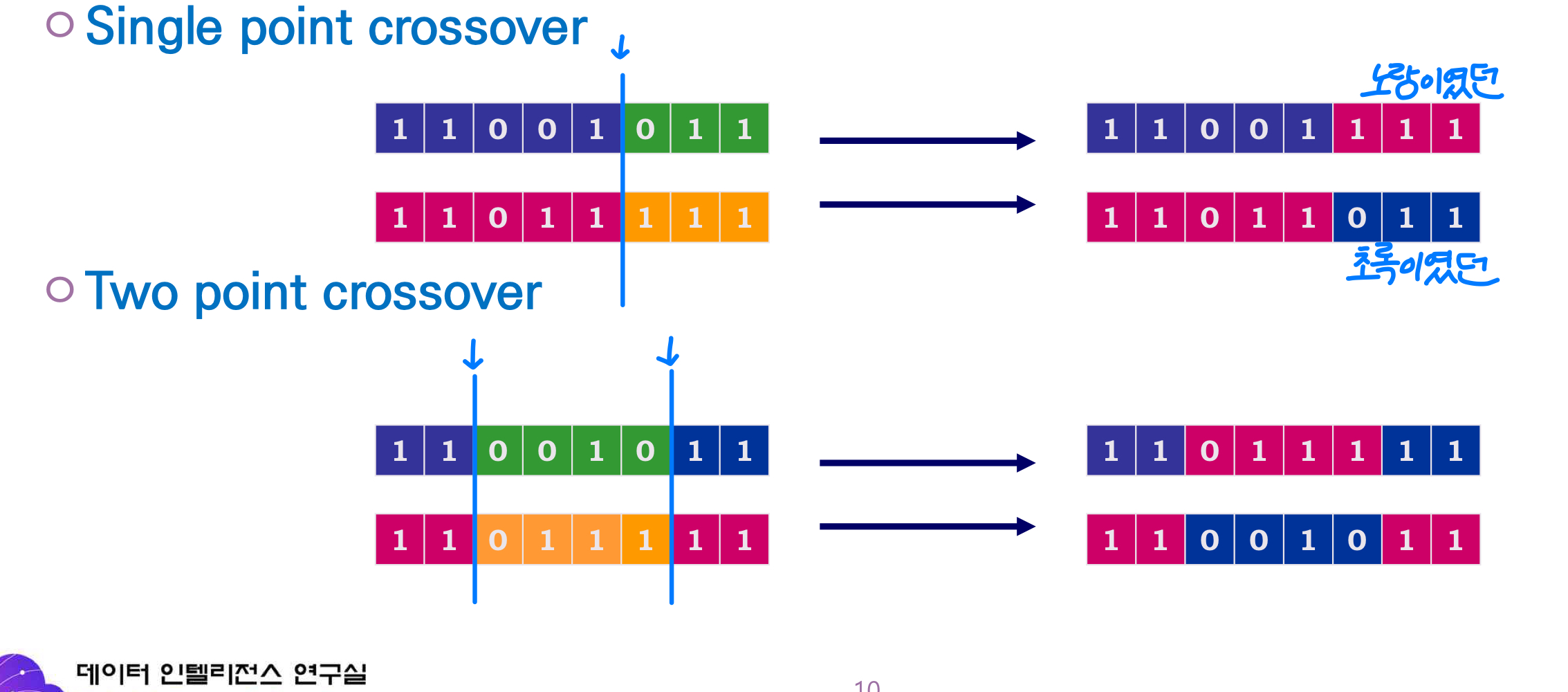
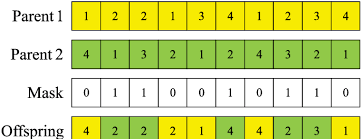
- uniform CX : 교차점을 따로 정하지 않고, 각 위치마다 확률적으로 부모 중 한쪽의 값을 선택하는 방법으로, 유전자 단위로 독립적 교환이 일어남. (Mask 설정 필요)
돌연변이 연산자
돌연변이 연산자는 개체의 유전자를 일정 확률로 변화시켜 새로운 염색체를 만드는 과정을 의미한다. 이는 개체군의 다양성을 유지하는 것을 목적으로 하는 연산자로, 유전자의 위치를 바꾸거나 값을 수정하는 형태로 진행하여, 지역 최적해가 아닌 전역 최적해를 찾을 수 있도록 해준다.
ELITISM
ELITISM이란, 현재 세대에서 가장 적합한 염색체를 수정 없이 다음 세대에 그대로 복사하는 방법으로 교차나 돌연변이 과정에도 손실되지 않고 보존된다는 특징이 있다.
이는 지금까지의 결과를 계속 활용할 수 있으므로 결과를 더 빨리 찾아낼 수 있으나, 결과의 다양성을 보장하지 못한다는 단점이 존재한다. (가장 적합한 방안이 계속 유전 -> 다른 해를 탐색할 기회 감소 -> 최적이 답이 아니더라도 최종 해결 방안이 될 가능성이 존재함)
Genetic Algorithm Example 1
import random
# 파라미터
POPULATION_SIZE = 4 # 개체 집단 크기
MUTATION_RATE = 0.1 # 돌연변이 확률
SIZE = 5 # 하나의 염색체에서 유전자(비트) 개수
# 염색체 클래스
class Chromosome:
def __init__(self,g = None):
# 유전자는 리스트 (0/1)로 구현
# copy() 메소드 사용 이유는 새로운 염색체의 유전자 리스트가 원본 리스트와 독립적으로 동작하도록 하기 위함
# 다시 말해, 새 염색체에서 genes를 변경해도 원본 리스트가 함께 바뀌지 않게 하기 위함임.
self.genes = g.copy() if g else []
self.fitness = 0 # 적합도 초기값
# 초기 염색체면 무작위로 0/1 채움
if len(self.genes) == 0:
for _ in range(SIZE):
# 0~1 사이 무작위 난수 생성하고, 이 난수가 0.5 이상이면 1, 그렇지 않으면 0을 유전자로 추가
self.genes.append(1 if random.random() >= 0.5 else 0)
def cal_fitness(self):
"""적합도 : 이진수 -> 10진수 값"""
# 유전자를 하나의 이진수로 보고 십진수로 변환해 적합도로 사용
# (ex) [1, 0, 1, 1, 1] -> value = 16 + 0 + 4 + 2 + 1 = 23
value = 0
for i in range(SIZE): # SIZE = 5 / i = 0, 1, 2, 3, 4
value += self.genes[i] * (2 ** (SIZE - 1 - i))
self.fitness = value
return self.fitness
def __str__(self): # 객체를 문자열로 표현한 것을 반환하는 함수 (출력 시 보기 좋은 형태 위해)
# 이 함수가 없으면 <__main__.Chromosome object at 0x78eb5a744e00>와 같이 메모리 주소가 출력됨
return str(self.genes)
# 보조 함수 : 개체 집단 출력
def print_p(pop):
for i, x in enumerate(pop):
print("염색체 #", i, "=", x, " 적합도 =", x.cal_fitness())
print("")
# 선택 연산 (룰렛 휠)
def select(pop):
# 총 적합도 합 (개체의 적합도 계산)
max_value = sum(c.cal_fitness() for c in pop)
# 모두 0인 극단 상황 방지 - 모든 개체 적합도가 0이면 랜덤 선택
# 이 과정 안 해주면 pick = random.uniform(0, max_value)에서 0만 선택 -> 아무 개체도 선택 x
if max_value == 0:
return random.choice(pop)
# 룰렛 휠에서 화살표가 멈추는 지점
# max_value = sum(c.cal_fitness() for c in pop) 요기서 전체 적합도 합 구하고
# 밑의 코드에서 그 합 범위 안에서 임의 실수 하나를 뽑으니까
# 결론적으로 적합도에 비례한 룰렛 휠 구현이 됨
pick = random.uniform(0, max_value) # 0 이상 max_value 이하 임의 실수 반환
current = 0 # 누적 적합도 합
# 룰렛 휠에서 화살표가 어떤 조각(개체)에 속하는지 찾아 반환
for c in pop:
current += c.cal_fitness()
if current > pick: # 누적합 > pick이 되는 지점(구간 안에 들어왔을 때), 그 지점 값 반환
return c
return pop[-1] # pick이 마지막 구간에 떨어진 경우(위의 루프에서 아무 것도 선택 안 된 경우), 마지막 개체 반환
# 교차/돌연변이 연산
def crossover(pop):
# 부모 선택 연산 (룰렛 휠)
father = select(pop)
mother = select(pop)
index = random.randint(1, SIZE - 1) # 1 ~ SIZE -1, 교차점 정하기
# 교차점 기준 교차 연산
child1 = father.genes[:index] + mother.genes[index:]
child2 = mother.genes[:index] + father.genes[index:]
return (child1, child2)
def mutate(c):
# 각 비트에 대해 MUTATION_RATE로 무작위 치환
for i in range(SIZE):
# MUTATION_RATE = 0.1, random.random() -> 0.0 이상, 1.0 미만 실수 반환
if random.random() < MUTATION_RATE: # 돌연변이 발생 여부 결정
c.genes[i] = 1 if random.random() < 0.5 else 0 # 새 유전자 값 결정
# 메인 루프
population = [] # 세대
# 초기 염색체 생성하여 개체 집단 구성
for _ in range(POPULATION_SIZE):# POPULATION_SIZE = 4
population.append(Chromosome()) # 개체 집단 정의
# 세대 번호 및 출력
count = 0
population.sort(key=lambda x : x.cal_fitness(), reverse=True) # 적합도 순 정렬
print("세대 번호 = ", count)
print_p(population)
count = 1
while population[0].cal_fitness() < 31:
new_pop = []
# 선택 + 교차로 자식 생성 (부모 2 -> 자식 2, 인구 수 채울 때까지)
# 한 번의 교차로 자식 2개 생기니까 전체 염색체 수 유지하려고 POPULATION_SIZE // 2
# 나누지 않으면 세대별 염색체 수 8개 됨
for _ in range(POPULATION_SIZE // 2):
c1, c2 = crossover(population)
new_pop.append(Chromosome(c1))
new_pop.append(Chromosome(c2))
# 자식 세대로 교체 (깊은 복사 성격 유지)
population = new_pop.copy()
# 돌연변이 수행
for c in population:
mutate(c)
# 출력 전 정렬 (내림차순 : 적합도 큰 순)
population.sort(key = lambda x : x.cal_fitness(), reverse=True)
print("세대 번호 = ", count)
print_p(population)
count += 1
if count > 100: # 종료 조건 확인
breakGenetic Algorithm Example 2
# Core imports
import random
import math
import statistics
import itertools
from typing import List, Tuple, Callable, Optional, Sequence, Any
import matplotlib.pyplot as plt
# For reproducibility during demos
def set_seed(seed : int = 42):
random.seed(seed)
set_seed(1234)
# Parameter (modifiable)
# 개체 집단 크기, 최소 2개 이상(교차 위해), 짝수가 좋음 (세대 크기 유지 위해서 -> 앞에서 // 2 한 것 처럼)
POPULATION_SIZE = 50 # population size (>= 2, preferably even)
GENE_SIZE = 16 # # chromosome length (bits)
# ELITISM : 상위 몇 개의 개체는 수정 없이 그대로 다음 세대로 넘기는 것
ELITISM = 2 # 그 세대에서 가장 좋은 애는 남기는 거, Number of elites to carry over unchanged
MAX_GENERATIONS = 200
# Selection / crossover / mutation options
SELECTION_METHOD = "roulette" # 'roulette' or 'tournament'
TOURNAMENT_K = 3 # if selection = tournament
CROSSOVER_METHOD = "single" # 'single'(하나의 교차점 기준 교차) or 'uniform'(균등 선택)
CROSSOVER_RATE = 0.9 # probability to crossover a pair, 교차 확률
MUTATION_RATE = 0.01 # per-gene mutation probability, 돌연변이 확률
# 돌연변이 확률을 세대가 진행됨에 따라 점진적으로 감소시킬지 여부
ADAPTIVE_MUTATION = False # if True, linearly reduces mutation over tim
# Fitness goal : maximize integer value of binary, or use a custom function (이진수 정수 값 최대화 or 사용자 정의 함수)
# 이진 리스트 -> 정수
# << : left shift
# 현재 비트(b)를 이전까지의 비트 연산 결과(value)에 붙여서 누적 정수를 만들어가는 과정
def binary_to_int(bits : Sequence[int]) -> int:
"""Convert list of bit (MSB first) to integer."""
value = 0
for b in bits: # b = 현재 비트
value = (value << 1) | (1 if b else 0) # 비트 연산 -> 결과는 정수
return value
# 비트열의 정수값을 그대로 적합도로 사용함. (이진수가 클 수록 더 적합함)
def fitness_func(bits : Sequence[int]) -> float:
"""Example fitness : value of the 16-bit number (0..65535)."""
return float(binary_to_int(bits))
# 비트열로 포함 가능한 최대값 계산 (목표 최댓)
# GENE_SIZE = 16
TARGET_MAX = (1 << GENE_SIZE) - 1 # e.g., 65535 for 16 bits
# Individual & Population
class Individual:
"""Chromosome represented as a list of 0/1 integers."""
def __init__(self, genes: Optional[List[int]] = None):
# 유전자 리스트 (염색체 생성)
if genes is None:
self.genes = [1 if random.random() < 0.5 else 0 for _ in range(GENE_SIZE)]
else:
self.genes = genes.copy()
# 적합도 초기값
self.fitness: float = 0.0
self.evaluate() # 적합도 계산
def evaluate(self) -> float:
self.fitness = fitness_func(self.genes)
return self.fitness
# 현재 개체와 똑같은 유전자를 가진 새 개체 반환 (깊은 복사, 새 인스턴스 만들어 반환하므로)
def copy(self) -> 'Individual':
return Individual(self.genes)
# 출력 형식
def __repr__(self) -> str:
return f"Individual(fitness = {self.fitness:.1f}, genes={self.genes})"
# 처음 세대 만드는 함수 (초기 집단(population)을 랜덤하게 생성하는 단계)
def init_population(n:int) -> List[int]:
return [Individual() for _ in range(n)]
# Selection Operators
def selection_roulette(pop: List[Individual]) -> Individual:
total = sum(ind.fitness for ind in pop) # 모든 개체 적합도 합
# Handle edge case : if all fitness are zero, pick uniformly
# 모든 적합도가 0일 때 예외처리
if total == 0:
return random.choice(pop).copy()
# 룰렛 화살표 위치 정하기
pick = random.uniform(0, total)
# 룰렛 휠 구성 (매커니즘은 Original에서와 같음)
acc = 0.0
for ind in pop:
acc += ind.fitness
if acc >= pick:
return ind.copy()
# Fallback
return pop[-1].copy()
def select_tournament(pop: List[Individual], k:int = 3) -> Individual:
# pop : 개체 집단, k : 한 번의 토너먼트에 참여할 개체 수
# 전체 population에서 무작위로 염색체 k개 선택
sample = random.sample(pop, k)
best = max(sample, key=lambda x : x.fitness) # 가장 적합도 높은 염색체 선택
return best.copy() # 가장 적합도 높은 염색체 복사 (이유는 앞에서 다룬 copy 사용 이유와 같음)
# select method에 따른 함수 호출
def select(pop: List[Individual]) -> Individual:
if SELECTION_METHOD == "tournament":
return select_tournament(pop, TOURNAMENT_K)
return selection_roulette(pop)
# Crossover operators
def crossover_single(p1: Individual, p2: Individual) -> Tuple[Individual, Individual]:
# pick a split in [1, GENE_SIZE-1]
# 하나의 교차점 기준 교차 (앞에서 다룬 매커니즘과 같음)
point = random.randint(1, GENE_SIZE - 1)
c1 = p1.genes[:point] + p2.genes[point:]
c2 = p2.genes[:point] + p1.genes[point:]
return Individual(c1), Individual(c2)
# 균등 교차 - 모든 유전자 기준, 랜덤 확률 -> 일정 확률 이상이면 교차
def crossover_uniform(p1 : Individual, p2 : Individual) -> Tuple[Individual, Individual]:
c1, c2 = [], [] # 자식 염색체 유전자 리스트 초기화
for a, b in zip(p1.genes, p2.genes):
# 랜덤 난수 생성 -> 50% 확률로 교차
if random.random() < 0.5:
c1.append(a); c2.append(b) # 교차 X
else:
c1.append(b); c2.append(a) # 교차
return Individual(c1), Individual(c2)
def do_crossover(p1 : Individual, p2: Individual) -> Tuple[Individual, Individual]:
# CROSSOVER_RATE = 0.9
# CROSSOVER_RATE 기준에 못 미치면 교차를 수행하지 않고, 기준에 미치면 교차 수행
if random.random() > CROSSOVER_RATE:
# no crossover -> copy parents
return p1.copy(), p2.copy()
# crossover method에 따른 호출 (uniform, multipoint)
if CROSSOVER_METHOD == "uniform":
return crossover_uniform(p1, p2)
return crossover_single(p1, p2)
# Mutation operators
def mutate(ind : Individual, gen_idx : int, max_gen : int) -> None:
# adaptive mutation : linearly decay over generations
# 돌연변이 확률을 세대가 진행됨에 따라 점진적으로 감소시킬지 여부에 따른 분기
if ADAPTIVE_MUTATION:
rate = MUTATION_RATE * max(0.01, 1.0 - gen_idx / max(1, max_gen))
else:
rate = MUTATION_RATE
for i in range(GENE_SIZE):
if random.random() < rate:
# 비트 반전 (1 - 0, 1 - 1 이런 형태가 되니까 비트 반전됨)
ind.genes[i] = 1 - ind.genes[i]
ind.evaluate() # 돌연변이 후 적합도 재계산
# GA Main Loop
def run_ga(max_generations: int = MAX_GENERATIONS, verbose : bool = False):
pop = init_population(POPULATION_SIZE) # 개체 집단 초기화
pop.sort(key=lambda x : x.fitness, reverse=True) # 적합도 높은 순 정렬
best_history = [pop[0].fitness] # 세대별 최고 적합도
mean_history = [statistics.mean(ind.fitness for ind in pop)] # 세대 평균 적합도
generation = 0
# 조건 : 세대 수가 최대에 도달하지 않고, 목표 적합도에 도달하지 않음
while generation < max_generations and pop[0].fitness < TARGET_MAX:
new_pop : List[Individual] = [] # 새 세
# Elitism : carry top ELITISM individuals
# ELITISM 개수만큼 상위 개체 그대로 다음 세대에 복사해서 유지
elites = [pop[i].copy() for i in range(min(ELITISM, len(pop)))]
new_pop.extend(elites)
# Fill the rest with offspring / 나머지 자식 채우기
while len(new_pop) < POPULATION_SIZE:
# 부모 선택
p1 = select(pop)
p2 = select(pop)
# 교차 연산
c1, c2 = do_crossover(p1, p2)
# 돌연변이 연산 및 자식 추가
mutate(c1, generation, max_generations)
if len(new_pop) < POPULATION_SIZE:
new_pop.append(c1)
if len(new_pop) < POPULATION_SIZE:
mutate(c2, generation, max_generations)
new_pop.append(c2)
# 세대 교체 및 정렬
pop = new_pop
pop.sort(key=lambda x : x.fitness, reverse=True)
# Track stats / 통계 갱신 및 세대 수 증가
best_history.append(pop[0].fitness)
mean_history.append(statistics.mean(ind.fitness for ind in pop))
generation += 1
# verbose가 참일 때, 10세대마다, 또는 목표 적합도 도달 시 출력하도록 함
if verbose and (generation % 10 == 0 or pop[0].fitness == TARGET_MAX):
print(f"Generation {generation} | Best : {pop[0].fitness} mean = {mean_history[-1]:.1f}")
return pop[0], best_history, mean_history, generation
# Quick smoke test
best, best_hist, mean_hist, gens = run_ga(verbose=True)
print("Best fitness : ", best.fitness, "in", gens, "generations")
Hyperparameter Sweep 분석
Example 1과 Example 2는 Selection 연산의 구현 방식(토너먼트, 룰렛 휠), ELITISM 존재 여부, 교차 및 돌연변이 확률을 결정하는 하이퍼파라미터 여부 등의 차이가 있다. (코드에 대한 자세한 설명은 주석에 있으므로 생략한다.)
여기서는 CROSSOVER_RATE, MUTATION RATE 값 차이에 따른 결과 변화에 대해 알아본다.
# c_rate=(0.6, 0.8, 0.95) : 실험할 CROSSOVER_RATE
# m_rates=(0.001, 0.01, 0.05): 실험할 MUTATION_RATE
# repeats=5 : 각 조합을 몇 번 반복할지
# max_generations=150 : 최대 세대 수
from re import M
def experiment_sweep(c_rate=(0.6, 0.8, 0.95), m_rates=(0.001, 0.01, 0.05), repeats=5, max_generations=150):
"""
Run multiple GA trials over combinations of crossover and mutation rates.
Returns summary dict with average generations to reach target (or last gen best).
"""
global CROSSOVER_RATE, MUTATION_RATE
results = {}
for c in c_rate:
for m in m_rates:
gens_list = []
best_at_end = []
for _ in range(repeats):
# reset seed each run for fair comparison
set_seed(random.randint(1, 10_000_000)) # 랜덤 시드 고정
# CROSSOVER_RATE, MUTATION_RATE 설정
CROSSOVER_RATE = c
MUTATION_RATE = m
# 실행
best, best_hist, mean_hist, g = run_ga(max_generations=max_generations, verbose=False)
gens_list.append(g)
best_at_end.append(best.fitness)
results[(c,m)] = {
'avg_generations' : sum(gens_list)/len(gens_list),
'avg_best_fitness' : sum(best_at_end)/len(best_at_end),
'runs' : len(gens_list)
} # 실험 결과 저장
return results
# Run a quick sweep (reduce repeats if slow)
sweep_results = experiment_sweep()
for (c, m), stats in sweep_results.items():
print(f"CROSSOVER={c:.2f}, MUTATION={m:.3f} -> avg_gens={stats['avg_generations']:.1f}, avg_best={stats['avg_best_fitness']:.1f}")분석 결과
교차율(CROSSOVER_RATE)이 너무 높으면, 탐색이 과도해져 수렴이 늦어지고, 0.6과 같이 적당할 때 빠르게 안정화되었다. 또한, 돌연변이율(MUTATION_RATE)은 너무 작으면 다양성이 부족하고, 너무 크면 무작위성이 커져 수렴 속도가 느려진다.
아래의 실행 결과를 살펴보면, CROSSOVER=0.95, MUTATION=0.001일 때, 다시 말해 교차율이 너무 높고, 돌연변이율이 너무 작을 때 탐색이 과도해져 수렴 속도가 느려졌다.
CROSSOVER=0.60, MUTATION=0.001 -> avg_gens=22.8, avg_best=65535.0
CROSSOVER=0.60, MUTATION=0.010 -> avg_gens=24.6, avg_best=65535.0
CROSSOVER=0.60, MUTATION=0.050 -> avg_gens=22.2, avg_best=65535.0
CROSSOVER=0.80, MUTATION=0.001 -> avg_gens=40.2, avg_best=65535.0
CROSSOVER=0.80, MUTATION=0.010 -> avg_gens=35.8, avg_best=65535.0
CROSSOVER=0.80, MUTATION=0.050 -> avg_gens=31.2, avg_best=65535.0
CROSSOVER=0.95, MUTATION=0.001 -> avg_gens=42.6, avg_best=65535.0
CROSSOVER=0.95, MUTATION=0.010 -> avg_gens=29.2, avg_best=65535.0
CROSSOVER=0.95, MUTATION=0.050 -> avg_gens=27.8, avg_best=65535.0# Visualize sweep (heatmap-like via scatter)
# We'll map x=CROSSOVER_RATE, y=MUTATION_RATE, size=avg_best_fitness, annotation=avg_generations
# 점이 클 수록 적합도가 높고, 숫자가 작을 수록 빠르게 수렴한 것임.
xs, ys, sizes, texts = [], [], [], [] # x축(crossover_rate), y축(mutation_rate), size(평균 최고 적합도, 점 크기), texts(평균 세대 수)
for (c, m), st in sweep_results.items():
xs.append(c)
ys.append(m)
sizes.append(st['avg_best_fitness'])
texts.append(st['avg_generations'])
plt.figure()
plt.scatter(xs, ys, s=[v for v in sizes])
for x, y, t in zip(xs, ys, texts):
plt.text(x, y, f"{t:.0f}", ha='center', va='bottom')
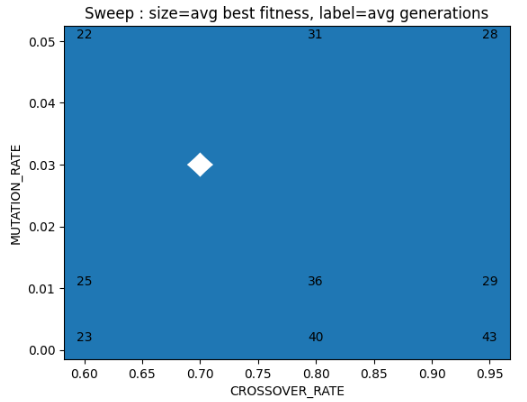
plt.title("Sweep : size=avg best fitness, label=avg generations")
plt.xlabel("CROSSOVER_RATE")
plt.ylabel("MUTATION_RATE")
plt.show()분석 결과
여기서 점이 클 수록 적합도가 높고, 숫자가 작을 수록 빠르게 수렴한 것이다.
모든 실험 조합이 전역 최적해(65535)에 도달했지만, 교차율과 돌연변이율의 조합은 수렴 속도에 뚜렷한 차이를 보였다.
특히, 교차율이 지나치게 높거나 돌연변이율이 너무 낮을 경우 탐색이 과도하거나 다양성이 부족해 수렴이 지연되었으며, 반대로 교차율 0.6, 돌연변이율 0.05 부근에서 가장 빠르고 안정적인 수렴을 보였다.