특징 공간과 결정 공간

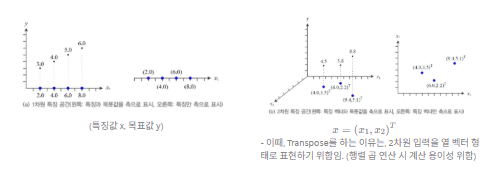
 특징 공간(Feature Space)이란, 데이터의 각 샘플이 가진 여러 특징(feature)들을 좌표로 표현하는 다차원 공간이다. 쉽게 말해, 특징들이 수치회된 벡터 공간이라고 할 수 있다. 머신러닝에서는 데이터가 특징 공간 내의 점(벡터)으로 표현되며, 모델이 패턴과 관계, 군집 등을 찾아내고 학습할 수 있도록 한다.

 이러한 특징 변수가 1개이면 1차원의 특징 공간, 2개이면 2차원의 공간, 세 개면 3차원의 공간, N개이면 N차원의 공간이 형성된다. 이러한 특징 공간을 표현할 땐, 특징과 목푯값을 함께 축으로 표시할 수도 있고, 특징만을 축으로 표현할 수도 있다.

 결정 공간(Decision Space)이란, 결과 값에 따라 나눠질 수 있는 공간으로, 모델이 입력 x를 받아 결과를 도출하는 공간을 의미한다. 이는 최종 Output 결정하는 공간이며, 특징 공간의 점이 어떤 클래스에 속하는지 표현한다. 이러한 결정 공간 안에서 클래스를 구분하기 위해선 결정 경계를 활용한다.

 결정 경계(Decision Boundary)란, 머신러닝의 특징 공간 안에서 분류 모델이 각기 다른 클래스(범주)의 데이터를 나누는 기준이 되는 선, 면, 혹은 초평면을 의미한다. 쉽게 말해, 서로 다른 클래스에 속하는 데이터들을 구분하기 위한 경계라고 할 수 있다.

 이러한 결정 경계는 특징 공간의 차원에 따라 다른 이름으로 불린다.

• 결정선 (Decision Line) : 2차원 결정 공간에서 사용되며, 결정 경계가 선 형태로 나타남.
• 결정면 (Decision Plane) : 3차원 결정 공간에서 사용되며, 결정 경계가 평면 형태로 나타남.
• 결정 초평면 (Decision Hyperplane) : 3차원보다 큰 결정 공간에서 사용되며, 시각적으로 그릴 순 없지만, 수학적으로는 n-1차원의 초평면이 존재하여 n차원 공간 데이터를 나눔. 다시 말해, 결정선과 결정면을 고차원으로 일반화한 개념임.

 이러한 특징 공간과 결정 공간은, 같은 공간일수도 있고, 아닐 수도 있다. 모델의 각 층이 만들어 내는 특징 공간이 연속적으로 이어지다가 마지막 층에서 결정 공간으로 귀결되기도 하고, 최종 특징 공간에서의 표현이 결정 함수에 의해 변환되어 특징 공간과 결정 공간이 다르게 표현되기도 하기 때문이다.

 분류 모델의 목표는 결국 최적의 결정 경계를 찾는 것이며, 모델이 학습을 한다는 것은 주어진 데이터를 가장 잘 나눌 수 있는 결정 경계(선, 면, 초평면)의 위치와 형태를 찾아가는 과정이라고 할 수 있다.

정리 )

• 특징 공간 : 입력 데이터가 존재하는 공간으로, 각 축이 입력 변수에 대응함.
• 결정 공간 : 모델이 특징 벡터 x를 결정 함수 f(x)를 통해 출력으로 사상시킨 공간 (다시 말해, 모델이 내린 분류 결과들이 표현된 공간)
• 결정 경계 : f(x) 값이 클래스 간 임계점에 해당하는 지점들의 집합

차원의 저주 (Curse of dimensionality)

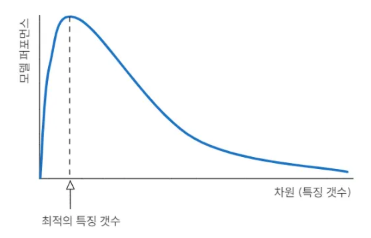
 차원의 저주(Curse of dimensionality)란, 학습 데이터에 비해 입력 차원의 수가 큰 경우 일정 차원을 기점으로 학습 능력이 급격히 감소하는 현상을 의미한다. 다시 말해, 특징 공간의 차원이 증가하면서 학습 데이터의 수가 특징 공간의 차원의 수보다 적어져 성능이 저하되는 것이다.

 차원이 증가할 수록 특징 공간의 부피가 커지고, 개별 차원 내에서의 데이터의 밀도가 희소해지며, 이에 따라 거리 함수가 제대로 작동하지 않고, 계산 비용이 증가하는 등의 문제가 발생하는데, 이러한 문제를 차원의 저주라고 한다.

 그러나, 입력 차원 수가 증가한다고 반드시 차원의 저주가 발생하는 것은 아니며, 학습 데이터보다 입력 차원의 수가 많아지는 경우에 차원의 저주 문제가 발생한다. 공간이 희소해짐에 따라, 저차원 데이터에서 패턴을 파악하는 것보다 고차원 데이터에서 패턴을 파악하는데 더 많은 데이터가 필요해지기 때문이다.

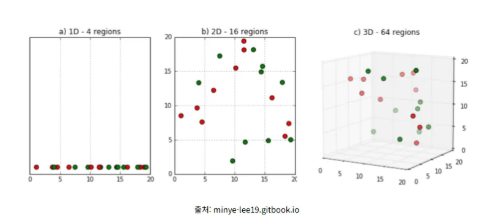
 이러한 차원의 저주는 차원이 증가함에 따라 동일한 데이터 개수로는 공간을 충분히 채울 수 없게 되어 데이터의 분포가 희소해지기에 발생한다. 입력 데이터의 차원이 증가하면, 특징 공간의 부피가 차원에 따라 기하급수적로 증가하여 데이터 간 거리가 멀어지고, 학습 데이터의 밀도가 낮아진다.

 이러한 차원의 저주 문제를 해결하기 위한 이론적인 해결책은 훈련 샘플의 밀도가 충분히 높아질 때까지 데이터를 모아서 훈련 세트의 크기를 키우는 것이다. 그러나, 일정 밀도에 도달하기 위해 필요한 훈련 샘플 수는 차원의 수가 커짐에 따라 기하급수적으로 늘어난다는 문제가 존재한다. 따라서 PCA, SVD 등과 같은 차원 축소 기법들을 통해 학습 결과에 영향을 미치지 않는 불필요한 축을 줄임으로써 차원의 저주를 완화하기도 한다.

정리 )

• “A function defined in high-dimensional space is likely to be much more complex than a function defined in a lower-dimensional space, and those complications are harder to discern” – Friedman
• This means that a more complex target function requires denser sample points to learn it well!