기계학습
1.특징 공간과 차원의 저주

특징 공간(Feature Space)이란, 데이터의 각 샘플이 가진 여러 특징(feature)들을 좌표로 표현하는 다차원 공간이다. 쉽게 말해, 특징들이 수치회된 벡터 공간이라고 할 수 있다. 머신러닝에서는 데이터가 특징 공간 내의 점(벡터)으로 표현되며, 모델이 패
2.과대적합, 규제, Bias-Variance Trade-off
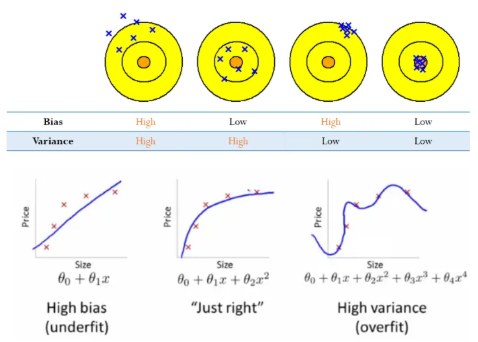
모델 선택과 과대적합 선형 회귀 (Linear Regression) 선형 회귀란, 두 번수 x, y에 대한 n개의 측정 값(ex. $(x1, x1), (x2, y2), … (xn, yn)$)이 있을 때, 주어진 가설(Hypothesis)에 대한 비용(Co
3.Eigen-Decomposition, PCA, SVD
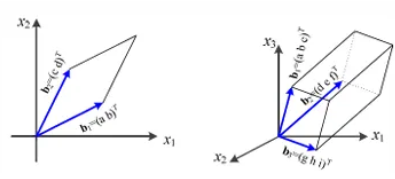
벡터 : 방향과 크기를 갖는 대상행렬 : 여러 벡터를 열로 담은 구조행렬은 교환법칙이 성립하지 않는다. ($AB ≠ BA$)행렬은 분배법칙과 결합법칙이 성립한다.$A(B + C) = AB + AC$ (분배법칙), $A(BC) = (AB)C$ (결합법칙)행렬의 곱셈을 위
4.서포트 벡터 머신과 결정 트리
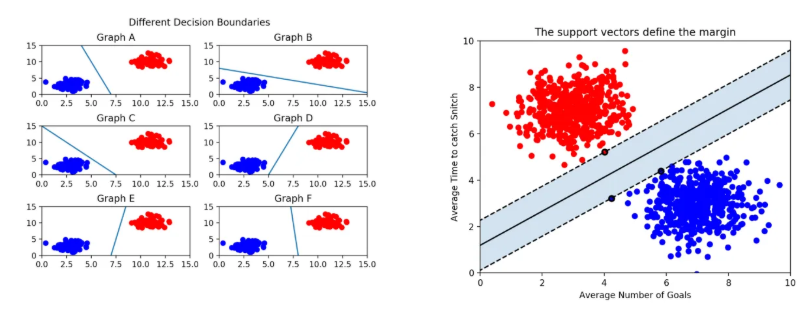
서포트 벡터머신은 선형/비선형 분류, 회귀, 이상치 탐색 등 복잡한 분류 문제에 적합한 다목적 기계학습 모델로, 중간 이하 크기의 데이터셋에 적합한 방법이다. 이는 분류를 위한 최적의 결정 경계를 찾는 것을 목표로 하며, 최적의 결정 경계라는 것은 다수의 결정 경계
5.앙상블과 랜덤 포레스트
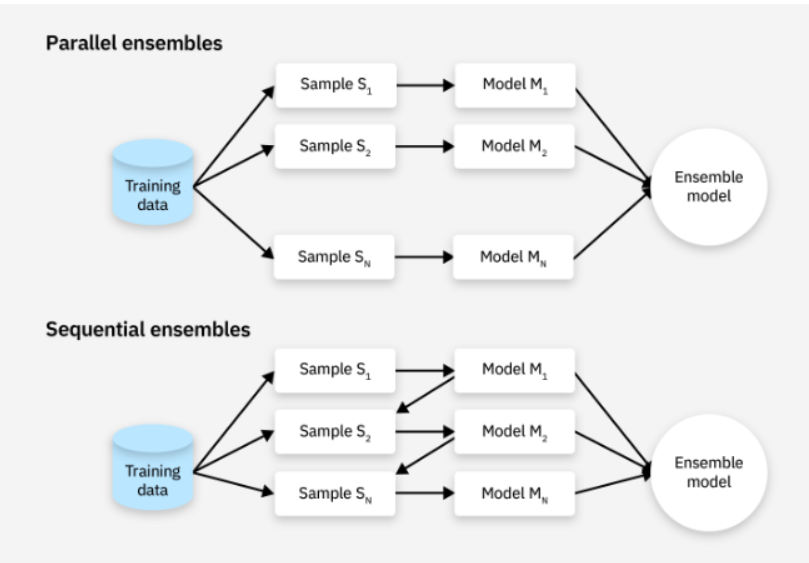
앙상블 기법이란, 여러 개 분류기를 생성하고, 그 예측을 결합함으로써 보다 정확한 예측을 도출하는 기법으로, Strong Classifier를 사용하는 대신 Weak Classifier를 조합하여 더 정확한 예측을 수행한다. 이는 단일 모델의 예측을 평가하는 것보다
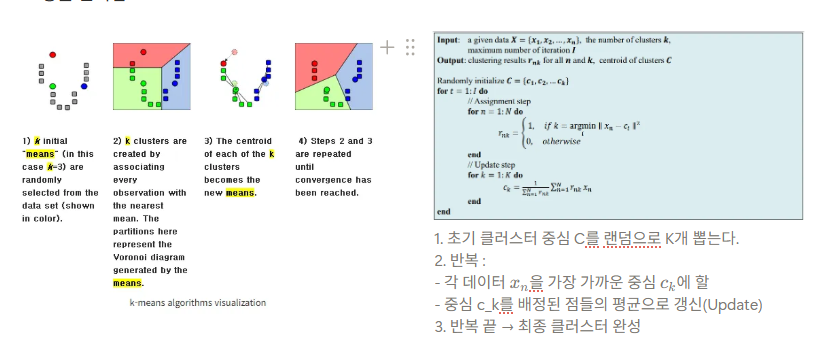
6.주성분분석과 군집화
차원의 저주(Curse of dimensionality)란, 학습 데이터에 비해 입력 차원의 수가 큰 경우 일정 차원을 기점으로 학습 능력이 급격히 감소하는 현상을 의미한다. 다시 말해, 특징 공간의 차원이 증가하면서 학습 데이터의 수가 특징 공간의 차원의 수보다 적