Deleting a Data Entry from B+ Tree

• Start at root, find leat L where entry belongs
• Remove the entry
  • If L is at least half-full, done!
  • Otherwise, L has only d-1 entries,
    • Try to re-distribute, borrowing from sibling(adjacent noces with same parent as L).
    • If re-distribution fails, merge L and sibling. Note merged node has at most 2d-1 entreis.
• If merge occured, must delete entry (pointing to L or sibling) from parent of L.
• Merge could propagate to root, decreasing height

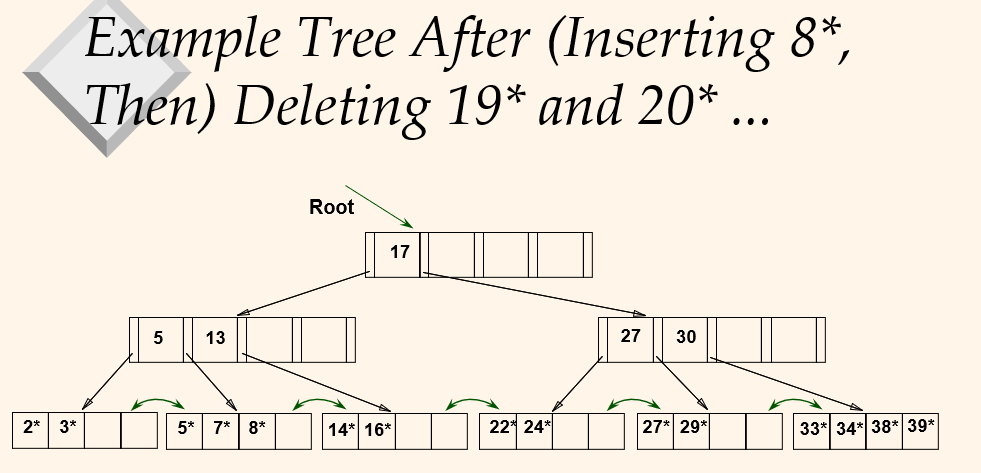
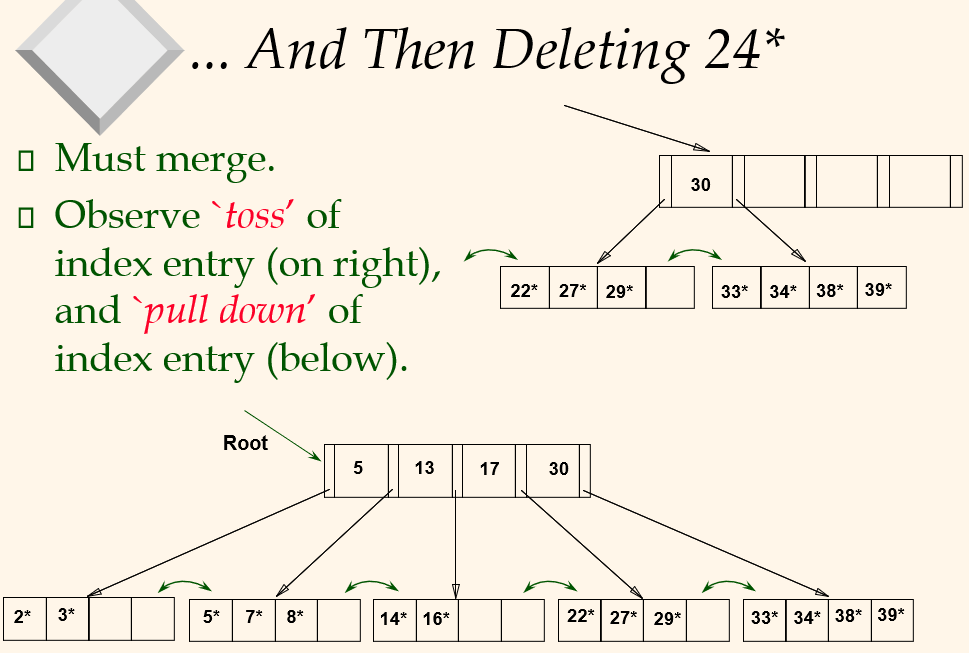
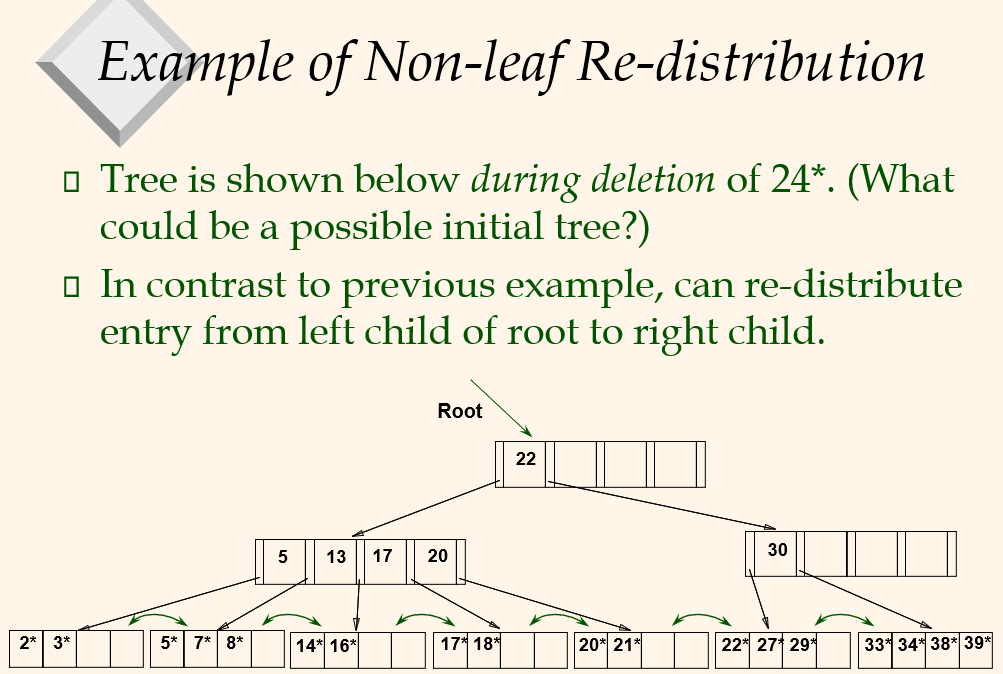
이것은 완전한 상태가 아니다. 30만 있는 페이지가 있다. redistribution이 일어날 것이다.

After Re-distribution

• Intuitively, entries are re-distributed by 'pushing through' the splitting entry in the parent node
• If suffices to re-distribute index entry with key 20; we've re-distributed 17 as well for illustration.
• Note how pointers for 16 and 22 are adjusted.
  

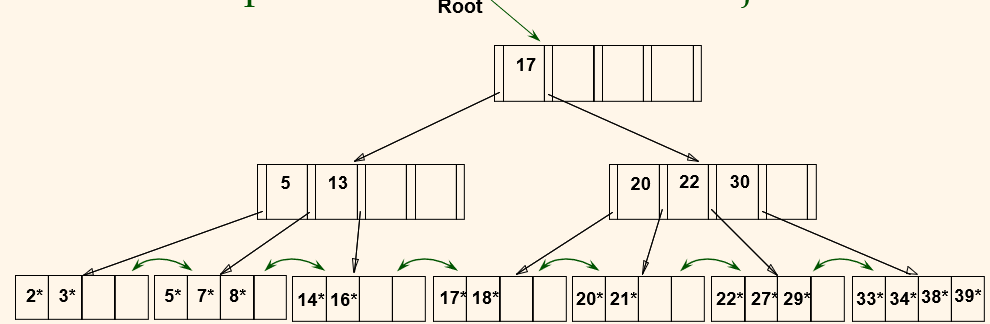
Bulk Loading of B+ Tree

• Loading the initial B+ tree by inserting one record at a time is very slow, and does not give sequential storage of leaves.
• Bulk Loading can be done much more efficiently.
• Initialization: Sort all data entries, insert pointer to first (leaf) page in a new (root) page.
  
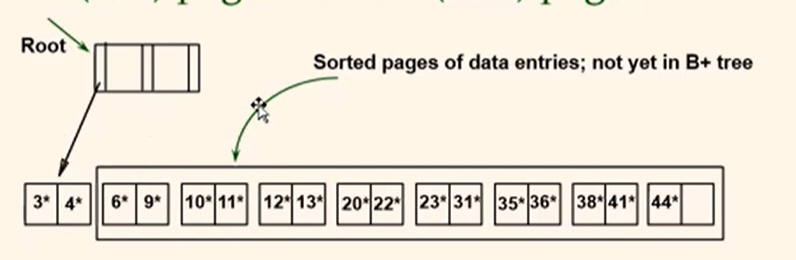
• Index entry for next leaf page always entered into right most index page just above leaf level. When this fills up, it splits along right-most path.
  
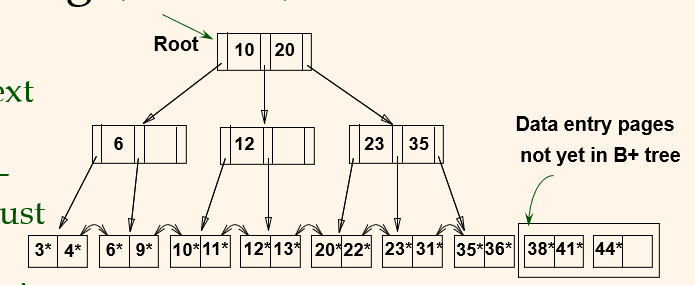
• Fewer I/Os during build. Leaves will be stored sequentially. Can control "fill factor" on pages.
  

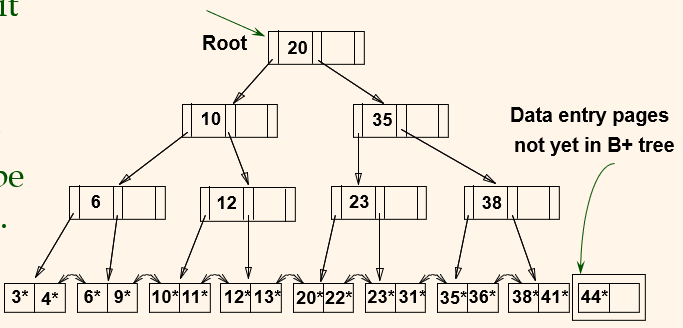
  이렇게 새로 넣으려는데 위에 노드에 가리키는 포인터가 없다면 그냥 44를 38 옆에 추가하고 44*를 가리키면된다.

A Note on 'Order'

• In practice, order (d) is replaced by physical space criterition (byte), i.e., 'at least half-full', for reasons below:
  • Index pages can typically hold many more entries than leaf pages. Why?
    -> Size of index entries typically smaller than size of data entries. Because index entries contains search key + page ID and data entries contain search key + RID. RID is much longer than page ID.
  • Variable sized records and search keys mean different numbers of entries in a node.
  • Alternative 3 leads to variable-sized data entries.

Summary

• Tree-structured indexes are ideal for range searches, also good for equality searches.
• ISAM is a static structure.
  • Only leaf pageas modified; overflow pages needed.
  • Overflow chains can degrade performance unless size of data set and data distribution stay constatnt.
• B+ tree is a dynamic structure.
  • Inserts/deletes leave tree height-balanced; log_FN cost.
  • High fanout (F) means depth rarely more than 3 or 4.
  • Almost always better than maintaining a sorted file.
  • Typically, 67% occupancy on average.
  • Preferable to ISAM, adjusts to growth gracefully.
  • If data entries are data records (Alternative 1), splits can change rids!
  • Bulk loading is much faster than repeated inserts for loading the B+ tree.
• Most widely used index in DBMMS. One of the most optimized components of DBMS.

Hash-Based Indexes (for Hashed Files)

Introduction

• As for any index, 3 alternatives for data entreis k*:
  1. <k, data record>
  2. <k, rid>
  3. <k, >
• k* are hashed (instead of sorted) on k
• Best for equality search. Cannot support range search
• Statid and dynamic hashing techniques exist; trades=off similar to ISAM vs B+ trees.

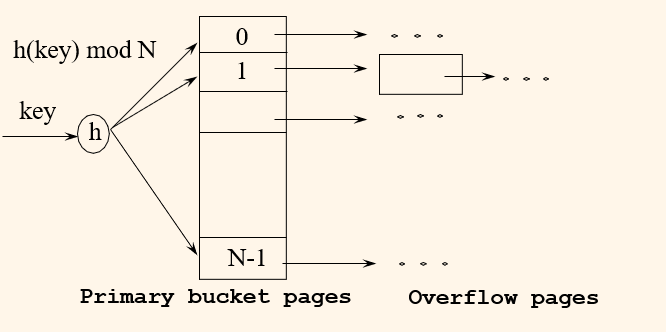
Static Hasing

• # primary pages fixed, allocaed sequentially, never de-allocated; overflow pages if needed
• h(k) mod N = bucket to which data entry k* belongs (N = # of buckets)
  

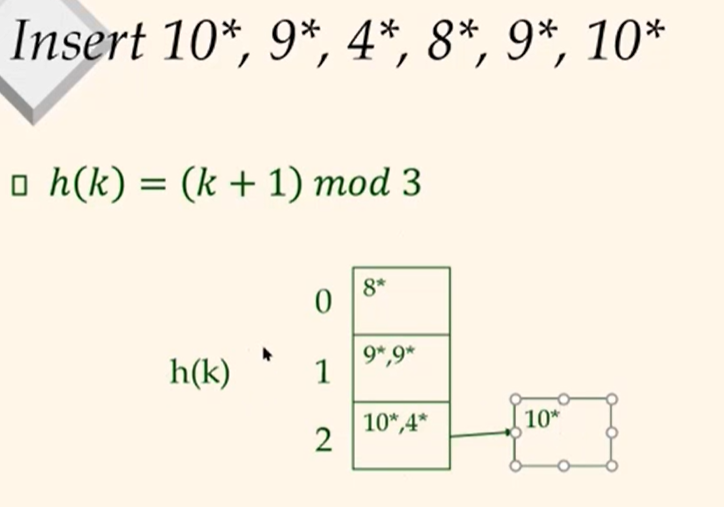
Insert 10*, 9*, 4*, 8*, 9*, 10*

Static Hashing (Contd.)

• Buckets contain data entries k*, in any of the 3 alternatives.
• Hash fn works on search key value k. Must distribute values over range 0 ... N-1, as evenly as possible.
  • h(k) = (a*k + b) usually works well.
  • a and b are constants; lots known about how to tune h.
• Long overflow chains can develop and degrade performance (when does this happen?)
  • Extensible and Linear Hashing: Dynamic techniques to fix this problem
• Buckets a primary page becomes full, why not dobule N, the # of bucekts?
  • Need to rehash all pages, too expensive!
• Idea: Use dictionary of pointers to buckets, double dictionary, split and rehash only the bucket that overflowed!\
  • Directory much smaller, so doubling is much cheaper.
  • Only one page is splited and rehased. No overflow page!
  • The trick lies in how to adjust the hash function!

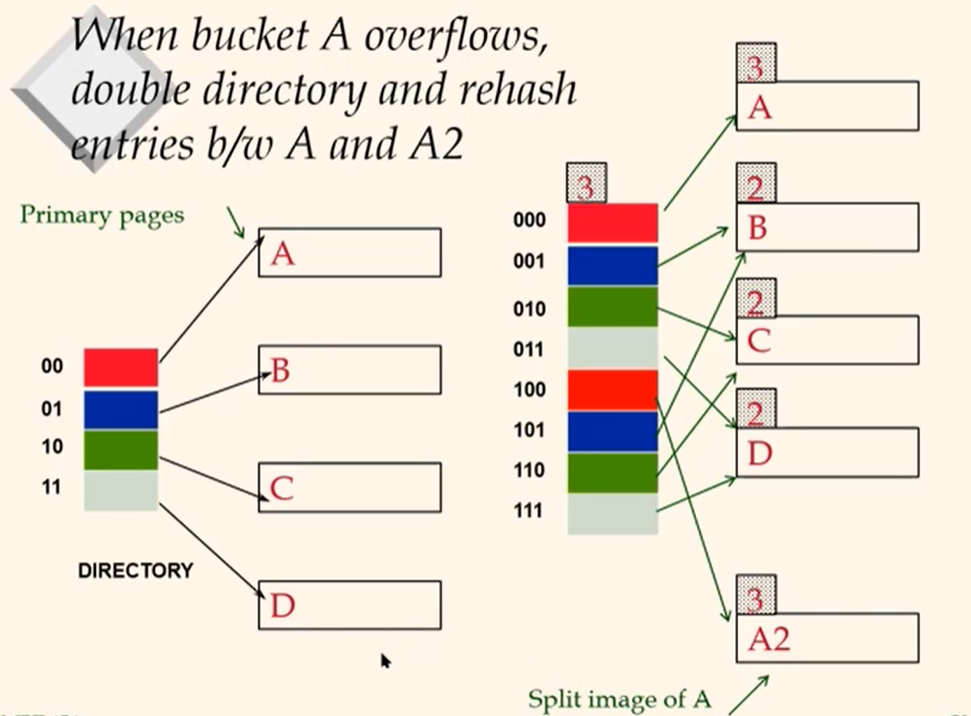
When bucket A overflows, double directory and rehash entries b/2 A and A2