B+ Tree: Most Widely Used Index
- Keep tree height-balanced. Search/insert/delete at log_f N cost(F = fanout (F is branch factor), N = # leafpages)
- Minimum 50% occupancy(except for root). Each node contains d <= m <= 2d entries. d is called the order of the tree.
- Supports equality and range-searches efficiently.
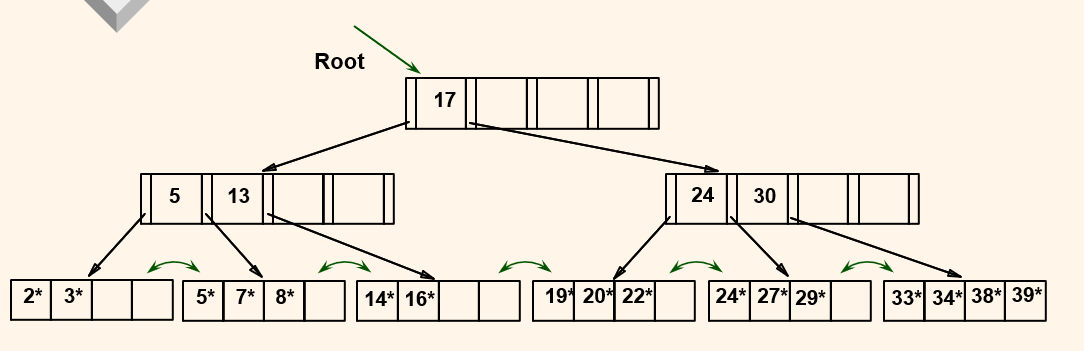
Example B+ Tree (d=2)
- Search begins at root, and key comparisons direct it to a leaf (as in ISAM)
- Search for
5*, 15*, all data entries >= 24*...
-> root에서 24를 찾은다음 24*로 간다. 그 다음은 가로로 연결된걸 따라서 간다.
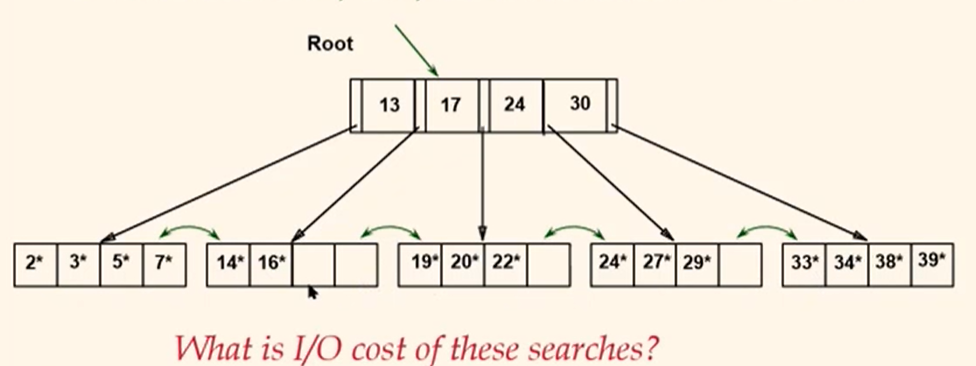
d =2 (Order) because every node has at least two entries.
- Based on the search for 15*, we know it is not in the tree!
- How about
17*?
-> index 노드에서 17 오른쪽을 따라 가지만 19*부터 시작한다. 따라서 없다. 17이 있다고 17*이 있다고 생각하면안된다. 17은 단지 인덱스 노드이다.
B+ Trees in Practice
- Assume page size 8KB and index entry size 40B. 8KB / 40B = 200 and d=100. For typical fill-factor 67%, fanout F = 67%*2d = 133
- Typical capacities:
- Height 4: 133^4 = 312,900,700 leaf pages
- Height 3: 133^3 = 2,352,637 leaf pages
- Can hold top levels in buffer pool:
- Level 1 = 1 page = 8KB
- Level 2 = 133 pages = 1MB
- Level 3 = 133^2 or 17,689 pages = 133MB

Insert/delete records
- Must maintain height-balancding and 50% minimum occupancy properties!
Inserting a Data Entry into B+ Tree
- Find correct leaf L
- Put data entry onto L
- If L has enough space, done!
- Else, must split L (into L and a new node L2)
- Redistribute entries envely, copy up middle key.
- Insert indexes entry for L2 into parent of L
- This can happen recursively at the parent
- To split an index node, redistribute entries evenly but push up middle key. (Constant with leaf splits)
- Splits "grow" tree: get wider or one level taller at
top when root splits.
Inserting 8* into Example B+ Tree
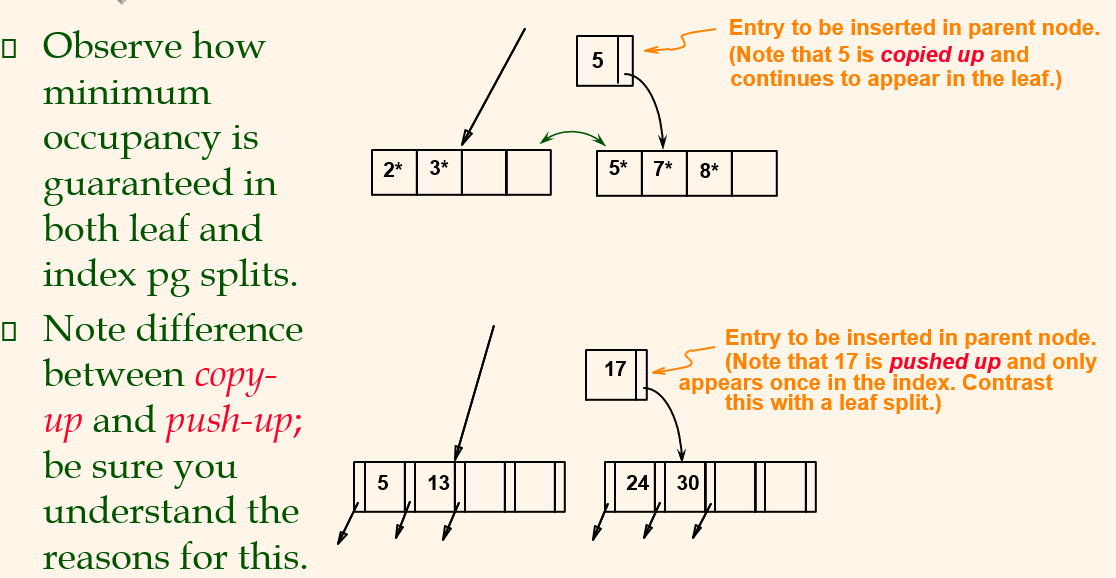
- 8을 넣는다고 했을 때 2,3,5,7,8중 5가 middle key이다. 5를 copy하는 이유는 5가 실제로 데이터를 가리키고 있기 때문이다. 그냥 move up하면 데이터가 없어질 것이다.
5*가 올라가면 13, 17, 24, 30 중 17이 middle key가 된다. 17은 실제 데이터가 없기 때문에 push up을 하는 것이다.
Example B+ Tree After Inserting 8*
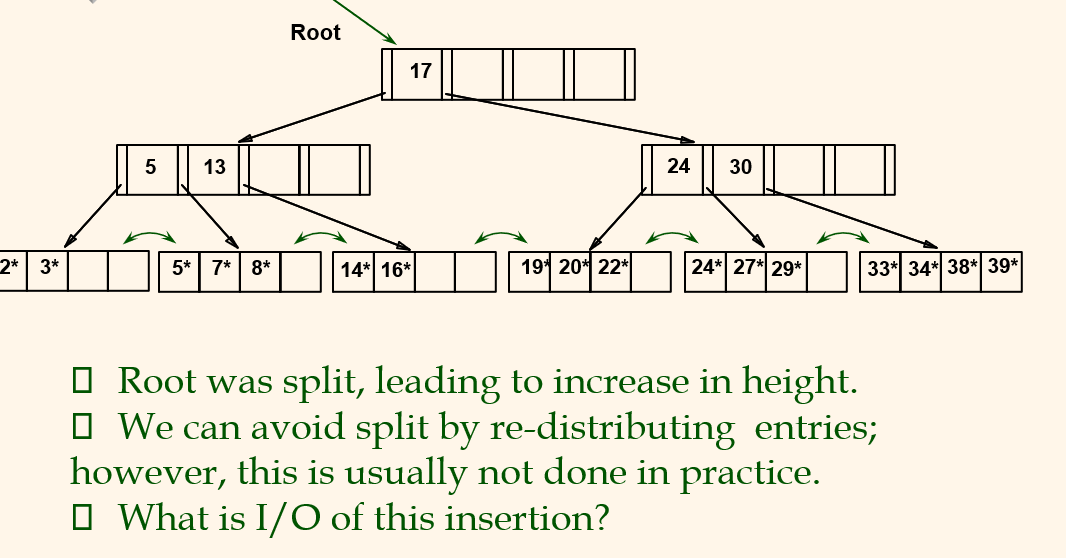
I/O cost of insert
- If insertion causes to split root of 4 level B+ tree, what is I/O cost of the insertion?
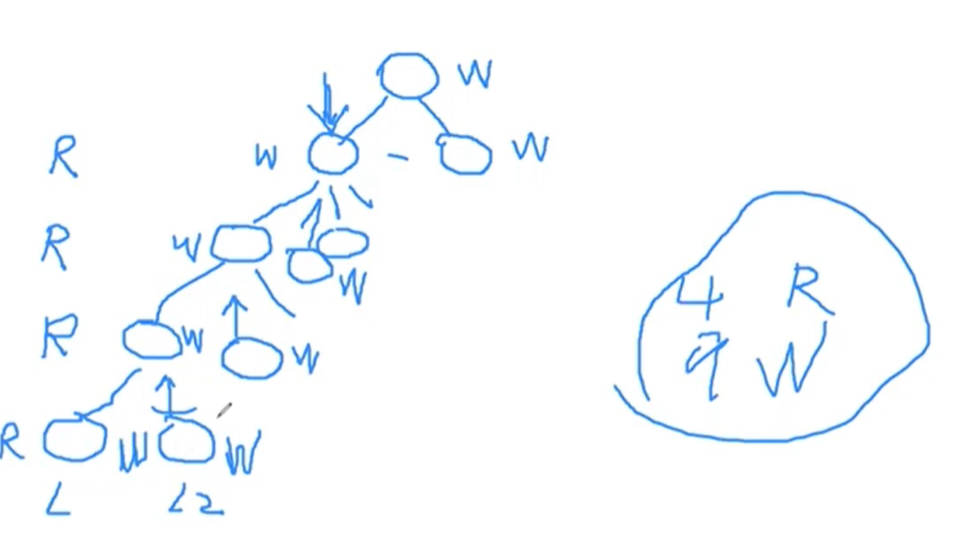
모든 층이 memory가 아닌 hard disk에 있다고 가정하자. 처음 아래로 향하는 화살표가 루트였을 때, 최악의 상황에서 insert를 할 경우 끝까지 타고내려간다. 여기서 4번의 R이 발생하고, 최악의 상황이니 split을 해야하니 왼쪽에 W, 오른쪽 W가 발생하고 이를 끝까지 타고 올라간다.
Deleting a Data Entry from B+ Tree
- Start at root, find leaf L where entry belongs
- Remove the entry
- If L is at least half-full, done1
- Otherwise, L has only d-1 entries,
- Try to re-distribute, borrowing from sibling (adjacent nodes with same parent as L).
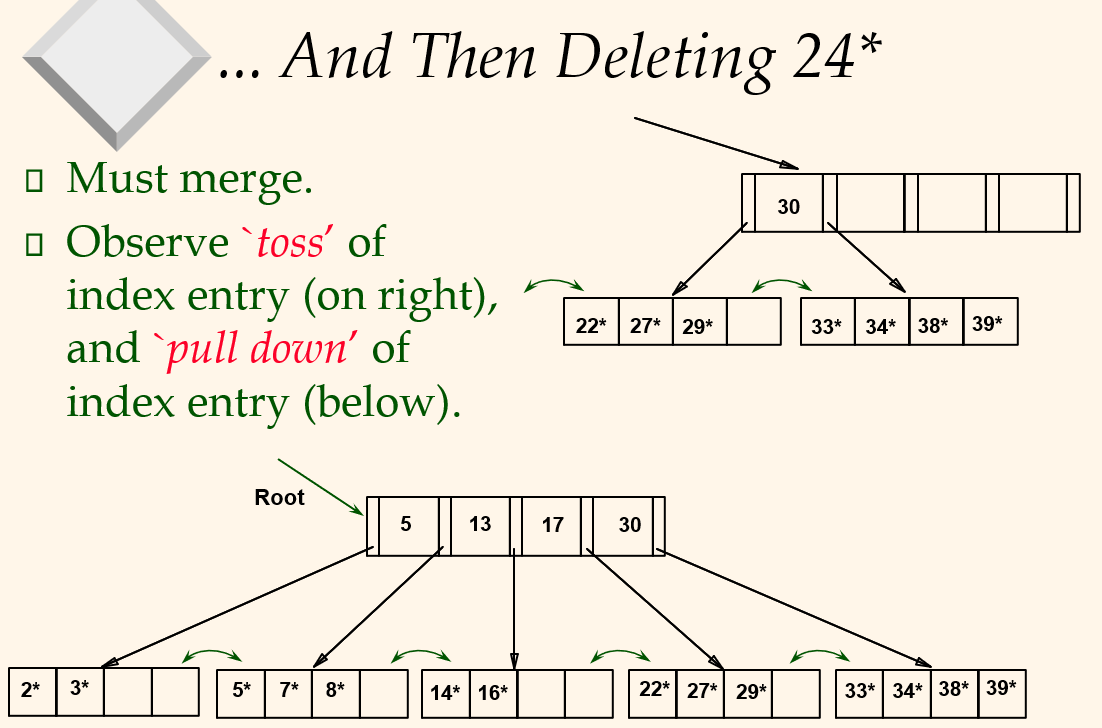
- If re-distribution fials, merge L and sibling. Note merged node has at most 2d-1 entries!
- If merge occurred, must delete entry (pointing to L or sibling) from parent of L.
- Merge could propagate to root, decreasing height.
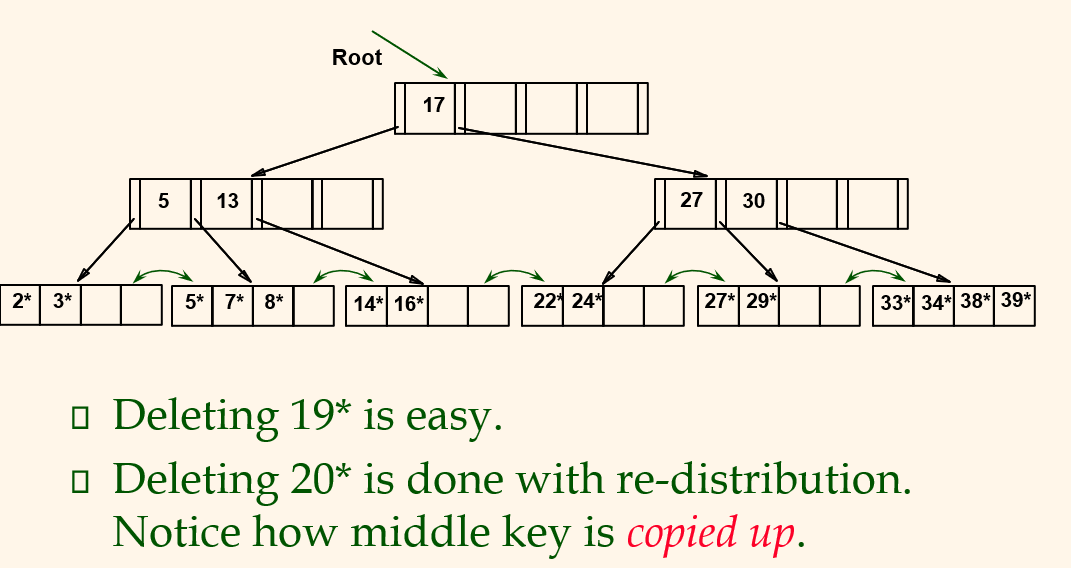
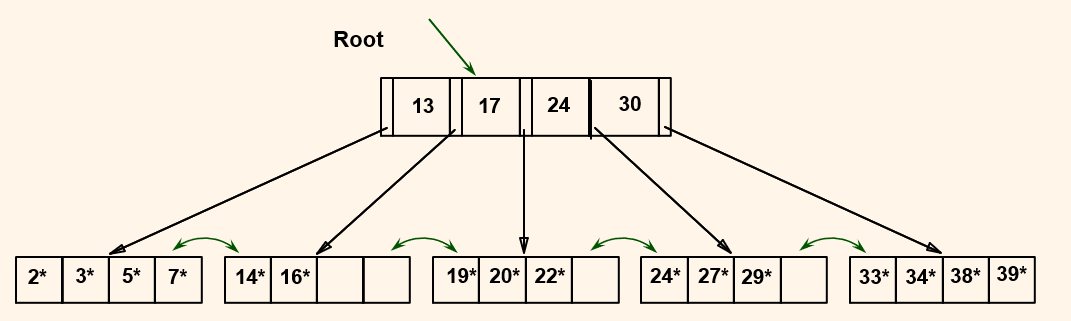
Example Tree After (Inserting 8*, Then) Deleting 19* and 20*...