2024.01.25 TIL - 리액트 숙련(Redux, 비동기, promise, REST), 알고리즘(유클리드 호제법)

Redux

• redux란 : 중앙 State 관리소, 전역 상태관리 라이브러리

• useState는 props 필요 -> prop drilling 발생
  -> 이를 방지하기 위해 등장한 Redux!

• 어떤 컴포넌트에서든지 state 접근, 제어 가능

• redux 설치

  • yarn add redux react-redux
    (package.jason에서 확인 가능)

비동기 프로그래밍

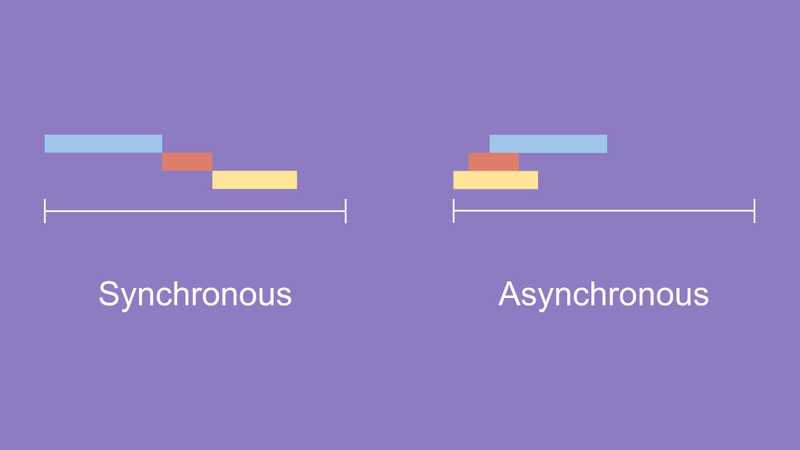
(이미지 출처 : 동기, 비동기 벨로그)

• 동기(Synchronous)적 프로그래밍 : 순차적 진행, 일반적으로 동기적

• 비동기(Asynchronous)적 프로그래밍 : 동시에 실행 (실행중인 코드의 완료 여부와 상관 없이 바로 다음코드로 넘어감)

  • setTimeout, addEventListener
  • 별도의 요청, 실행대기, 보류 등
  • ⭐️ 서버통신과 관련된 로직

• 비동기 통신의 단점 : 콜백함수 지옥

  • 해결책 : promise 객체!
  • 비동기 처리는 약속에 의해 움직임 -> 약속 관련 사항들이 promise 객체에 담김

• promise 객체에 담기는 주요 정보 3가지

  • 대기 상태(pending) : 요청하고 난 직후
  • 이행 상태(fulfilled) : 데이터 전달 성공적으로 완료한 상태
  • 거부 상태(rejected) : 데이터 전달 실패

• promise 객체 핸들링 방법 2가지

① then ~ catch (ES6)

axios.get('API url')	// promise 객체
.then(response => {})	// 성공적 처리시
.catch(error => {})		// 실패시
.finally(() => {})		// 성공, 실패와 무관하게 무조건 실행되는 부분

② async ~ await (ES7)

const getweather = async () => {	// async : 비동기로 처리할거야
  try {
  	const reponse = await axios.get('API url')	// await : 여기 실행한 다음 넘어가
    console.log('정상처리 : ' + response);
  } catch (error) {
    console.lgo('오류 발생 : ' + error)
  };
}

(await 안하면 API 제대로 받기도 전에 다음 console.log 실행해버려서 정상 처리가 안됨)

REST

• REST : REpresentational State Transfer
  • CRUD 할 수 있게 http method(get, post, put, delete)를 사용하여 요청보내는 것
    -> 자원은 특정 형태로 표현됨
• Restful 하다?! : 누가 보더라도 이해 쉽고, 사용 쉬운 REST API

알고리즘

문제 - 최대공약수, 최소공배수

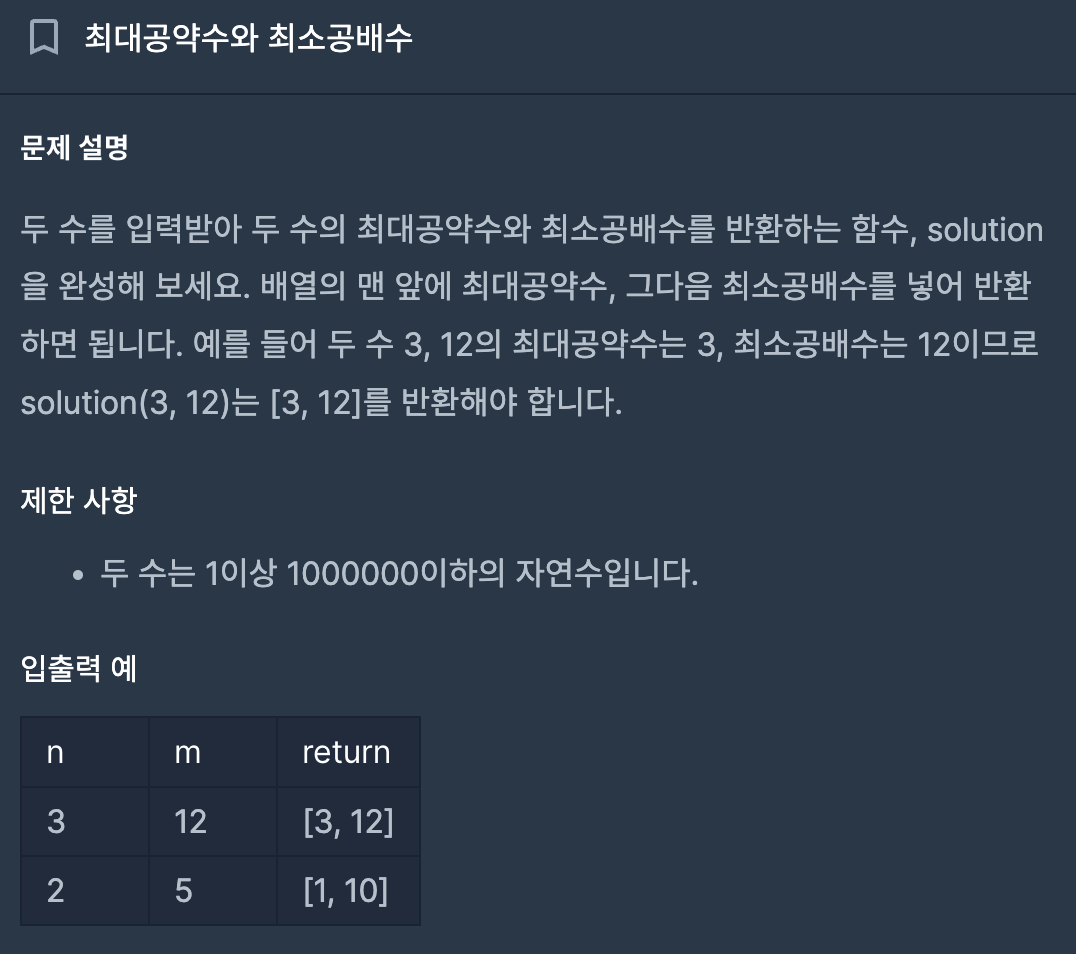
• 최대공약수, 최소공배수란?

  • 최대공약수 : 두 수가 서로 공통으로 가지고 있는 약수 중 가장 큰 수

    • 최대공약수(Greatest Common Divisor, GCD)
      두 수 a, b의 최대공약수는 gcd(a, b) 또는 (a, b)로 나타냄.

  • 최소공배수 : 두 수에 서로 공통으로 존재하는 배수 중 가장 작은 수

    • 최소공배수(Lowest Common Multiple, LCM)
      두 수 a, b의 최소공배수는 lcm(a, b) 또는 [a, b]로 나타냄.

(참고 : B의 개발 공부 기록)

유클리드 호제법

• 두 수의 최대공약수를 구하는 방법
  
  (이미지 출처 : 유클리드 호제법)

풀이

function solution(num1, num2) {
    const gcd = (a, b) => a % b === 0 ? b : gcd(b, a % b);
    const lcm = (a, b) => a * b / gcd(a, b);
    return [gcd(num1, num2), lcm(num1, num2)];
}

💡 두 수의 곱을 최대공약수로 나누면 최소공배수가 됨

🐣 오늘의 느낀점

오늘 배운 내용들은 대체로 js 문법 강의때부터 계속 듣던 내용들이고 팀 프로젝트에서도 다뤘던 내용들인데, 계속 들어도 여전히 어렵고 들을 땐 이해한 것 같다가도 막상 나중에 다시 돌이켜보면 이게 뭐였더라 싶고, 직접 쓰려고 하면 어떻게 쓰는거더라 하면서 영 내 것이 되지 않는 희한한 대목들이다. 그래도 계속 주입식 교육마냥 세뇌되듯이 계속 듣고 있자니 그래도 다행인지 귀에는 익어가는 것도 같다. 캠프 하면서 계속 듣는 내용들이지만 영 낯선 친구들이다.