👀 'Do it! 알고리즘 코딩테스트 with Python(김종관 저)'을 공부하고 정리한 내용입니다.

1. 개념

주어진 데이터의 구간 합과 데이터 업데이트를 빠르게 수행하기 위해 고안해낸 자료구조의 형태가 바로 세그먼트 트리입니다. 더 큰 범위는 '인덱스 트리'라고 불리는데, 코딩 테스트 영역에서는 큰 차이가 없다고 생각해도 됩니다.

세그먼트 트리의 종류는,

구간합, 최대·최소 구하기로 나눌 수 있고, 구현 단계는 트리 초기화하기, 질의값 구하기(구간합 또는 최대·최소), 데이터 업데이트하기로 나눌 수 있습니다.

2. 원리 이해하기

2-1. 트리 초기화하기

리프 노드의 개수가 데이터의 개수(N) 이상이 되도록 트리 배열을 만듭니다. 트리 배열의 크기를 구하는 방법은 ${2}^k \ge N$을 만족하는 k의 최솟값을 구한 후 $2^k*2$를 트리 배열의 크기로 정의하면 됩니다. 예를 들어 다음과 같은 샘플 데이터가 있다면 N=8이므로 $2^k \ge 8$이므로 배열의 크기를 $2^3*2=16$으로 정의합니다.

샘플데이터
{5, 8, 4, 3, 7, 2, 1, 5}

리프 노드에 원본 데이터를 입력합니다. 이때 리프 노드의 시작 위치를 트리 배열의 인덱스로 구해야하는데, 구하는 방식은 $2^k$를 시작 인덱스로 취하면 됩니다. 예를들어 k의 값이 3이면 start index = 8이 됩니다.

리프 노드를 제외한 나머지 노드의 값을 채웁니다.($2^k-1$부터 1번 쪽으로 쯕 채웁니다). 채워야하는 인덱스가 N이라고 가정하면 자신의 자식 노드를 이용해 해당 값을 채울 수 있습니다. 자식 노드의 인덱스는 이진 트리 형식이기 대문에 $2N, 2N+1$이 됩니다.

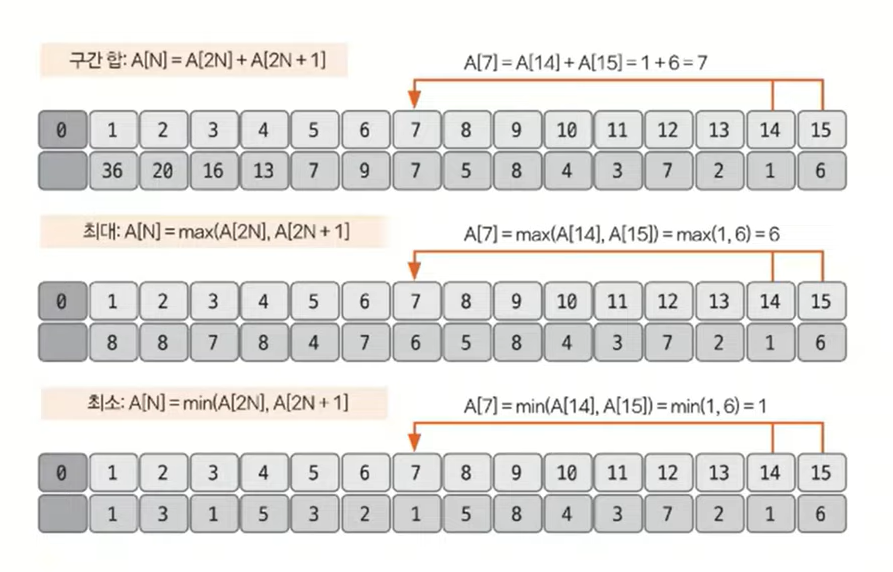
샘플을 이용해 3개의 케이스와 관련된 세그먼트 트리를 구성했습니다. 구성한 트리 배열을 실제 트리 모양으로 구조화하면 다음과 같이 표현할 수 있습니다.

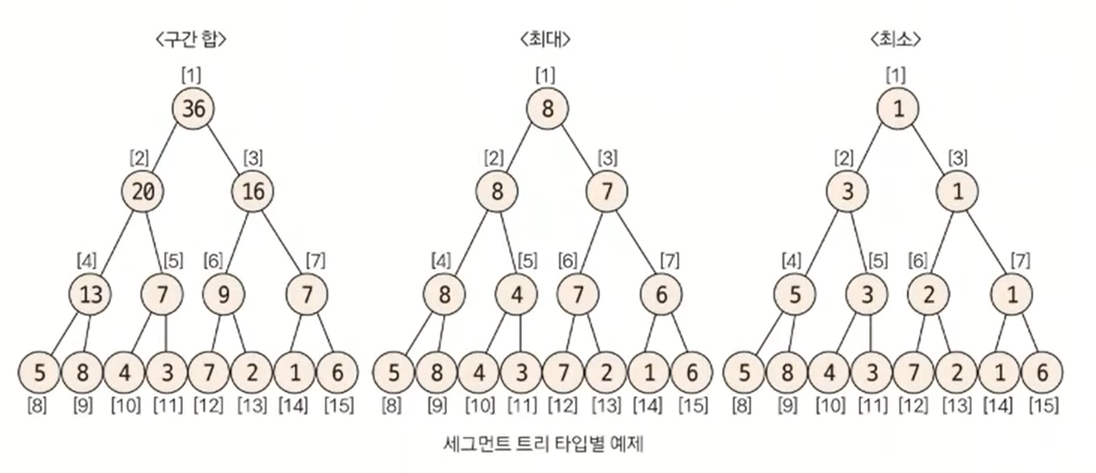
이렇게 세그먼트 트리를 구성해 놓으면 그 이후 질의와 관련된 결과값이나 데이터 없데이트 요구사항에 관해 좀 더 빠른 시간 복잡도 안에서 해결할 수 있게 됩니다.

2-2. 질의값 구하기

주어진 질의 인덱스를 세그먼트 트리의 리프 노드에 해당하는 인덱스로 변경합니다. 기존 샘플을 기준으로 한 인덱스 값과 세그먼트 트리 배열에서의 인덱스 값이 다르기 때문에 인덱스를 변경해야 합니다. 인덱스 변경 방법은 다음과 같습니다.

질의 인덱스를 세그먼트 트리 인덱스로 변경하는 방법
세그먼트 트리 index = 주어진 질의 index + $2^k$-1

질의값 구하는 과정
1. start_index % 2 == 1 일때 해당 노드를 선택한다.
2. end_index % 2 == 0 일때 해당 노드를 선택한다.
3. start_index depth 변경 : start_index = (start_index + 1) / 2 연산을 실행한다.
4. end_index depth 변경: end_index = (end_index - 1) / 2 연산을 실행한다.
1~4를 반복하다가 end_index < start_index가 되면 종료한다.

질의에 해당하는 노드 선택 방법

• 구간합: 선택된 노드를 모두 더함
• 최대값 구하기: 선택된 노드 중 max값을 출력
• 최소값 구하기: 선택된 노드 중 min값을 출력

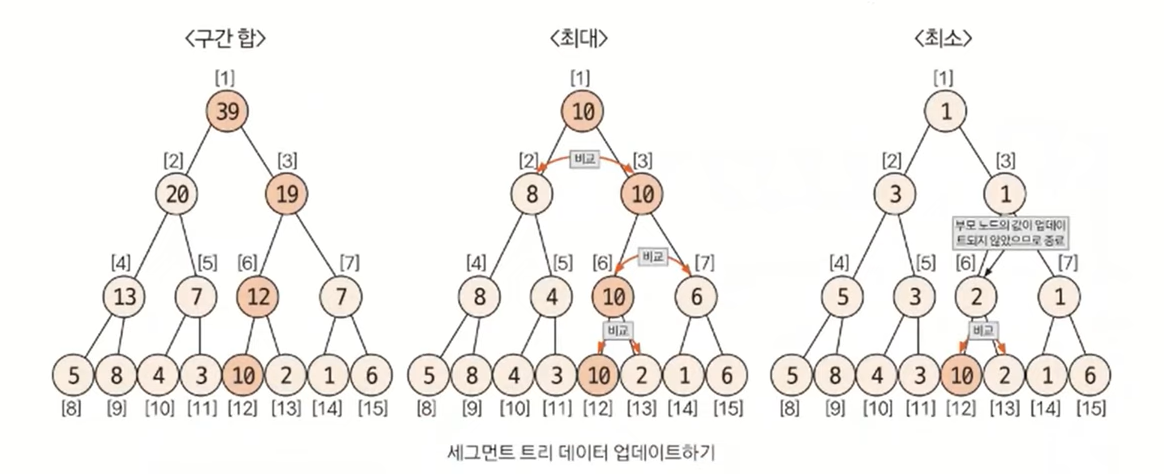
2-3. 데이터 업데이트하기

• 구간합의 경우, 원래 데이터와 변경 데이터의 차이만큼 부모 노드로 올라가면서 변경.

• 최대값 찾기의 경우, 변경 데이터와 자신과 같은 부모를 지니고 있는 다른 자식 노드와 비교해 더 큰 값으로 업데이트. 업데이트가 일어나지 않으면 종료.

• 최솟값 찾기의 경우, 변경 데이터와 자신과 같은 부모를 지니고 있는 다른 자식 노드와 비교해 더 작은 값으로 업데이트. 업데이트가 일어나지 않으면 종료.