[알고리즘] 정렬(insertion, bubble, selection, quick, merge, heap) - C++

정렬

정렬: sorting

• 지정한 기준에 맞게 정렬해서 출력하는 알고리즘

sort	inplace	시간 복잡도
insertion sort( 삽입 정렬 )	O	n^2
bubble sort(버블 정렬)	O	n^2
selection sort(선택 정렬)	O	n^2
quick sort(퀵 정렬)	O	average case: O(nlogn) / worst case: O(n^2)
merge sort(합병 정렬)	X	nlogn
heap sort(힙 정렬)	O	nlogn

⭐️ inplace sort : 정렬하는 데이터에 추가적 메모리 공간이 필요하지 않은 정렬

시간 복잡도: O(1) > O(nlogn) > O(N) > O(Nlogn) > O(n^2) > O(2^n) >O(n!) 의 순서

• O(1)일 때 가장 빠르다-> 효율이 좋은 알고리즘

insertion sort( 삽입 정렬 )

sorted와 key를 비교해 삽입 , 추가적인 메모리 공간 필요 없음, 시간복잡도 : O(n^2)

앞에서부터 혹은 뒤에서부터 차례대로 이미 정렬된 배열과 비교해 자신의 위치를 찾아서 삽입한다.

🎯EX

삽입 정렬은 정렬된 부분과 정렬되지 않은 부분이 나눠져 있는데 어떤 경우이던지 적어도 하나의 자료는 정렬되어 있다. -> 맨 앞(앞에서 부터 정렬), 혹은 맨 뒤(뒤에서 부터 정렬) 자료형은 정렬되어 있다고 생각할 수 있기 때문에 두번째 자료부터 key값으로 해서 정렬한다.

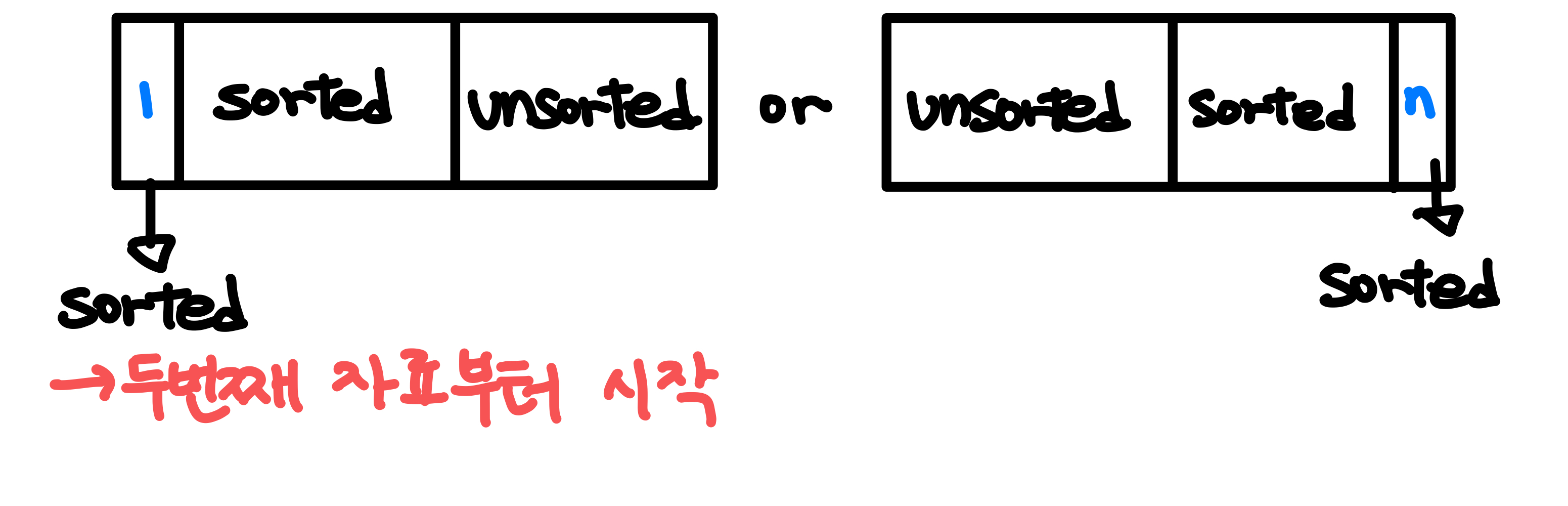
삽입 정렬의 방식에 따라 아직 정렬되지 않은 배열 8 5 6 4 2를 오름차순 정렬하면 과정은 다음과 같다.
1. 정렬된 배열 sorted에 속하는 8과 첫번째 key값이 될 5를 비교해 8과 5의 위치를 바꾼다.
5 8 6 4 2
2. 다음 key값인 6을 sorted에 속하는 8과 비교해 정렬한다.
다음으로 sorted에 속하는 5와 key값을 비교해 정렬한다.(5<6이므로 그대로)
5 6 8 4 2
3. 다음 key값인 4를 sorted에 속하는 8, 6, 4와 차례로 비교해서 정렬한다.
5 6 4 8 2 -> 5 4 6 8 2 -> 4 5 6 8 2
4. 다음 key값인 2를 sorted에 속하는 8, 6, 5, 4 와 차례로 비교해서 정렬한다.
4 5 6 2 8 -> 4 5 2 6 8 -> 4 2 5 6 8 -> 2 4 5 6 8
정렬 완료 : 2 4 5 6 8

구현 (c++)

#include <iostream>
#include <stdio.h>
using namespace std;

void insertNextItem(int a[], int i);
void insertionSort(int a[], int n)//precondition: a는 0부터 n-1까지 범위가 정해진 배열이다 
{
    int i;
    for (i = 1; i < n; i++) 
    {                       
        insertNextItem(a, i);
    }
}//array를 출력해주는 함수

int main()
{
    int length;
    cin >> length;
    int* array = new int[length];

    for (int i = 0; i < length; i++)
        cin >> array[i];
    insertionSort(array, length);
    for (int i = 0; i < length; i++)
        cout << array[i] << endl;

}
void insertNextItem(int a[], int i)
{   
    int newItem(a[i]);
    int insertPos(i);
    for (; insertPos && newItem < a[insertPos - 1]; insertPos--)
    {   
        a[insertPos] = a[insertPos - 1];
        a[insertPos] = newItem;
    }
}//array의 내용을 바꿔주는 함수(작은 수가 들어오면 밀고 큰 수가 들어오면 끝으로 밀기()

bubble sort(버블 정렬)

서로 인접한 두 원소를 검사하여 정렬 , 추가적인 메모리 공간 필요없음, 시간복잡도 : O(n^2)
selection sort와 유사

인접한 2개의 레코드를 비교하여 크기가 순서대로 되어 있지 않으면 서로 위치를 바꿈

selection sort와의 차이:

• selection sort: selcet한 것만 정렬한다.
• bubble sort: select 하지 않은 요소도 정렬해서 swapping 횟수가 증가한다.
  ( 데이터 이동 횟수가 많다.)

🎯EX

버블 정렬은 첫 번째 자료와 두 번째 자료를, 두 번째와 세 번째 자료를, 세 번째와 네 번째를, … 이런 식으로 (마지막-1)번째 자료와 마지막 자료를 비교하여 교환하면서 자료를 정렬한다.이런 버블 정렬의 방식에 따라 아직 정렬되지 않은 배열 8 5 6 4 2를 오름차순 정렬하면
1회전 : 1회전의 결과로 가장 큰 자료가 맨 뒤로 이동
2회전 : 맨 끝에 있는 자료는 정렬에서 제외되고, 2회전을 수행하고 나면 끝에서 두 번째 자료까지는 sorted에 포함되어 정렬에서 제외된다.
...
sorted에 포함되는 자료가 늘어나고 모든 자료가 포함되면 정렬이 완료된다.

구현 (c++)

void swapElements(int a[], int maxPos, int last)
{
    mytype temp = a[first];
    a[first] = a[last];
    a[last] = temp;
}
void bubbleSortPhase(int a[], int last)
{
    int pos;
    for (pos = 0; pos < last ; pos++)
        if (a[pos] > a[pos+1]) {
            swapElements(a, pos, pos+1);
        }

}
void bubbleSort(int a[], int n)
{

    int i;
    for (i = n - 1; i > 0; i--)
        bubbleSortPhase(a, i);
}

selection sort (선택 정렬)

가장 작은 or 큰 것을 찾아 현재 인덱스와 자리바꿈, 추가적인 메모리 공간 필요없음, 시간복잡도 : O(n^2)

배열에서 가장 작은(큰) 값을 찾아서 첫번째 요소와 교환, 두번째로 작은 값을 찾으며 반복해서 배열을 끝까지 정렬한다.

🌟 배열이 클수록 비효율적인 방법으로 크기가 작은 배열에 효율적이다.

최악의 경우 : 배열이 역순인 경우

배열이 역순인 경우 첫 순회에 n-1 번의 비교, 두번째 순회에 n-2 번의 비교...로 배열을 비교해 정렬하는 시간복잡도는 다음과 같다.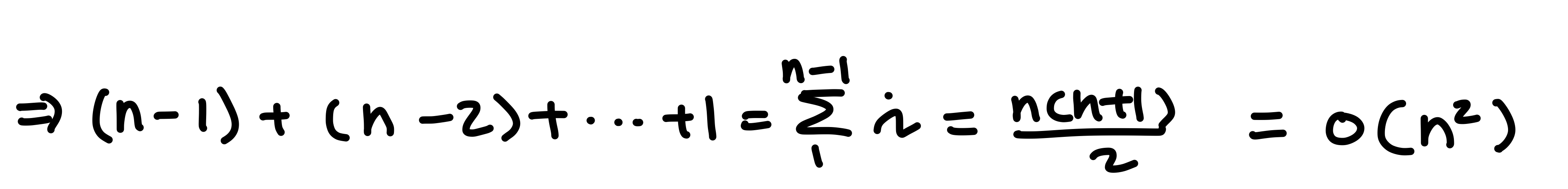

🎯EX

선택 정렬의 방식에 따라 아직 정렬되지 않은 배열 8 5 6 4 2를 오름차순 정렬하면
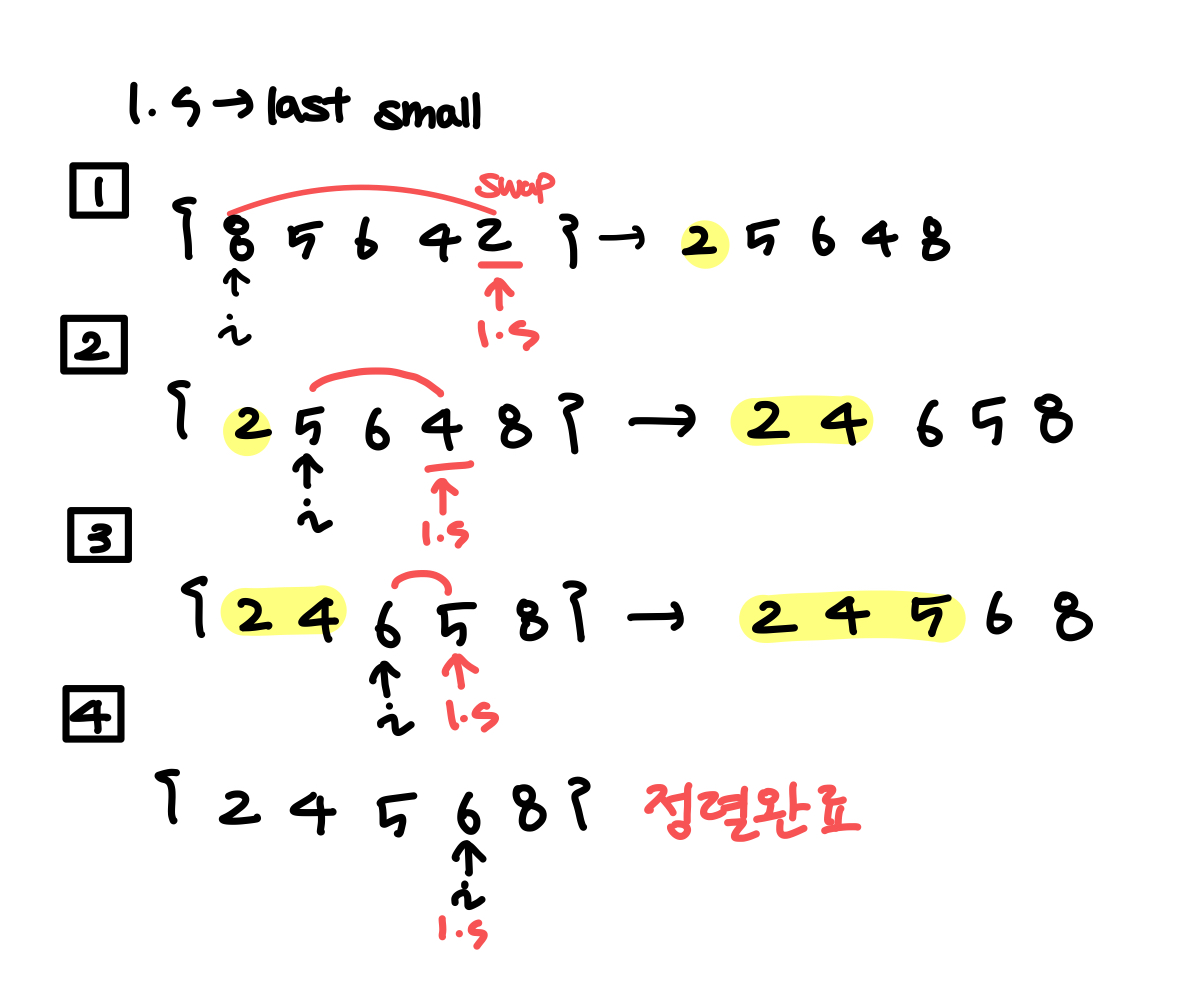매 회마다 맨 앞에서부터 인덱스 i 를 키워가며 배열에서 가장 작은 자료를 찾아 비교해서 인덱스의 위치를 교환한다. 교환해서 정렬된 부분을 sorted라 할 때 인덱스를 키워가며 sorted에 속하지 않는 범위에서 last small을 찾아 계속 교환하다보면 오름차순으로 정렬된다.

구현 (c++)

//selection sort increasing order로 구현
#include <iostream>
using namespace std;

void fillArray(int* a, int size, int& numberUsed);
void selectionSort(int a[], int n);
void swapValues(int& v1, int& v2);
int maxSelect(int a[], int n);

const int NSIZE = 10;

int main()
{
    cout << "Sorting program" << endl;
    int sampleArray[NSIZE], numberUsed;
    fillArray(sampleArray, NSIZE, numberUsed);
    selectionSort(sampleArray, numberUsed);

    cout << "Sorted results" << endl;
    for (int index = 0; index < numberUsed; index++)
        cout << sampleArray[index] << " ";
    cout << endl;

    return 0;
}

void fillArray(int* a, int size, int& numberUsed)
{
    int next, index = 0;
    cin >> next;
    while ((next >= 0) && (index < size))
    {
        a[index] = next;
        index++;
        cin >> next;
    }
    numberUsed = index;
}

void selectionSort(int a[], int n)
{

    int last(n - 1);
    int maxPos;
    while (last > 0)
    {
        maxPos = maxSelect(a, last + 1);
        swapValues(a[maxPos], a[last]);
        last--;
    }
}

void swapValues(int& v1, int& v2)
{
    int temp;
    temp = v1;
    v1 = v2;
    v2 = temp;

}

int maxSelect(int a[], int n)
{
    int maxPos(0), currentPos(1);
    while (currentPos < n) {
        // Invariant: a[maxPos] >= a[0] ... a[currentPos-1]
        if (a[currentPos] > a[maxPos])
            maxPos = currentPos;
        currentPos++;
    }
    return maxPos;
}

Quick sort(퀵 정렬)

대용량 데이터에 유리, 정렬 중 가장 짧은 시간복잡도를 갖는 편
시간 복잡도: 평균의 경우 O(nlogn), 최악의 경우 O(n^2)

기준이 되는 원소 피봇(pivot)을 기준으로 두 개 부분으로 나누어 정렬 후 합쳐서 전체 배열을 생성한다.

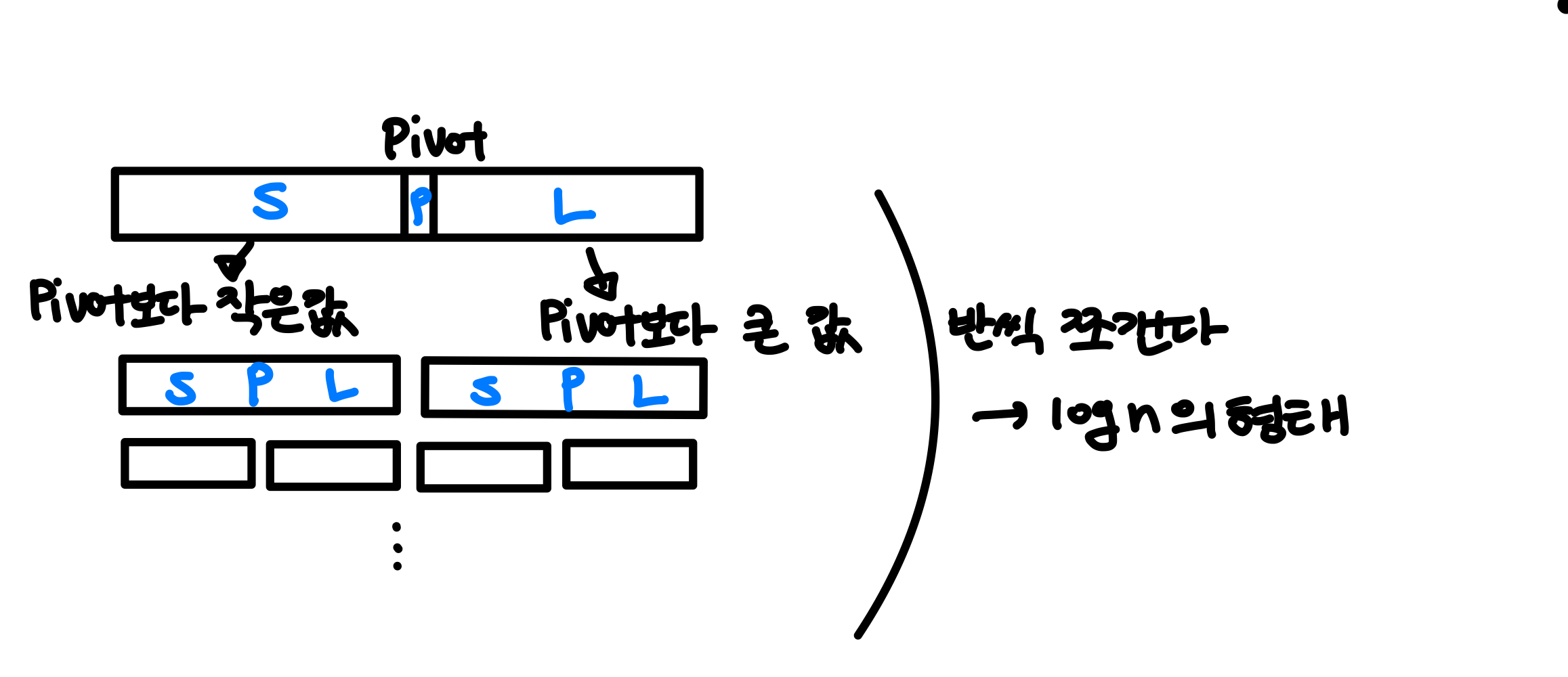
한 회전의 정렬을 마치면 pivot을 기준으로 왼쪽의 자료들은 전부 pivot보다 작고 오른쪽의 자료들은 전부 pivot보다 큰 상태로 정렬된다.

🎯EX

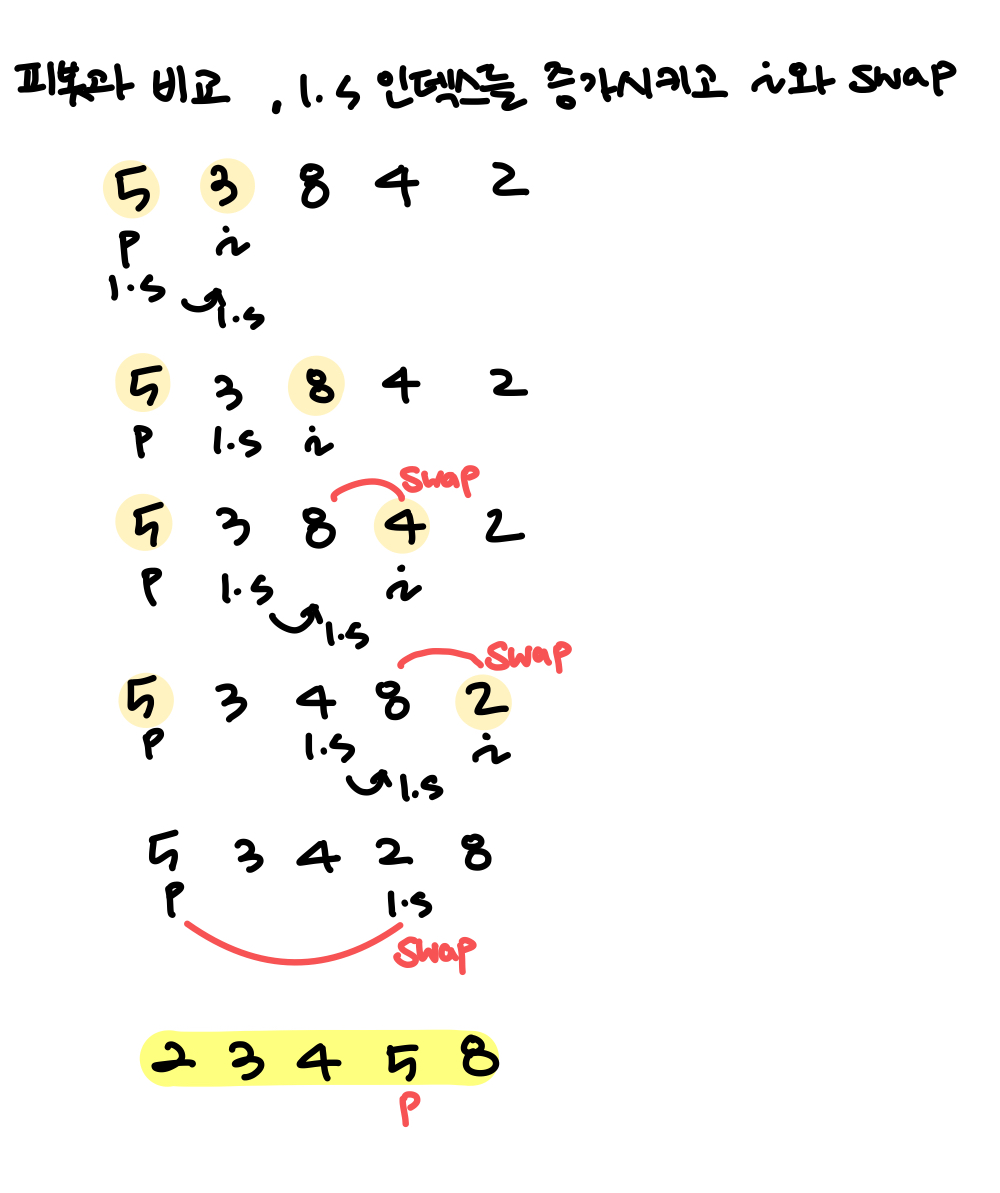
• 피봇을 맨 앞에 두어 pivot의 왼쪽은 pivot 보다 작은 요소 , 뒤는 pivot 보다 큰 요소로 정렬

1. pivot p, last small l.s 을 모두 첫번째 요소로 초기화한 상태에서 sorted에 속하지 않는 두 번째 인덱스부터 i 인덱스를 키워가며 비교
2. pivot 보다 i 가 작으면 l.s를 다음 인덱스로 증가시키고 i 와 l.s 를 교환
   🌟인덱스를 증가시키고 교환한다.
3. i인덱스가 배열 끝에 닿을 때 까지 진행하고 마지막에 pivot과 last small을 교환
4. 배열이 전부 정렬될 때까지 pivot을 첫번째 인덱스로 설정하며 같은 과정 반복
   

구현

#include <iostream>
using namespace std;
typedef int mytype;

int partition(mytype a[], int first, int last);
void quicksort(mytype a[], int first, int last);
void swapElements(mytype a[], int first, int last);

int n;

void swapElements(mytype a[], int first, int last)
{
    mytype temp = a[first];
    a[first] = a[last];
    a[last] = temp;
}

void quicksort(int a[], int first, int last)
{

    if (first >= last) 
        return;
    cout << "no partition:";
    for (int i = 0; i < n; i++) {
        cout << a[i] << " ";
    }
    cout << endl;
    int split(partition(a, first, last));
    cout << "partition: ";
    for (int i = 0; i < n; i++) {
        cout << a[i] << " ";
    }
    cout << endl;
    quicksort(a, first, split - 1);
    quicksort(a, split + 1, last);
}


int partition(mytype a[], int first, int last)
{
    int lastSmall(first), i;
    for (i = first + 1; i <= last; i++)
        // loop invariant: a[first+1]...a[lastSmall] <= a[first] &&
        // a[lastSmall+1]...a[i-1] > a[first]
        if (a[i] <= a[first]) { // key comparison
            ++lastSmall;
            swapElements(a, lastSmall, i);
        }
    swapElements(a, first, lastSmall); 
    return lastSmall; 
}
int main()
{
    mytype* a;
    cin >> n;

    a = new mytype[n];
    for (int i = 0; i < n; i++) {
        cin >> a[i];
    }
    cout << endl;

    quicksort(a, 0, n - 1);
    cout << "정렬된 배열: ";
    for (int i = 0; i < n; i++) {
        cout << a[i] << " ";
    }
}

Merge sort(합병 정렬)

왼쪽과 오른쪽이 정렬된 상태에서 merge(합치기), inplace sort가 아니다. 추가공간 필요

갯수가 1 or 0이 될 때까지 배열을 쪼개고 크기를 비교해서 자른 역순으로 합친다.

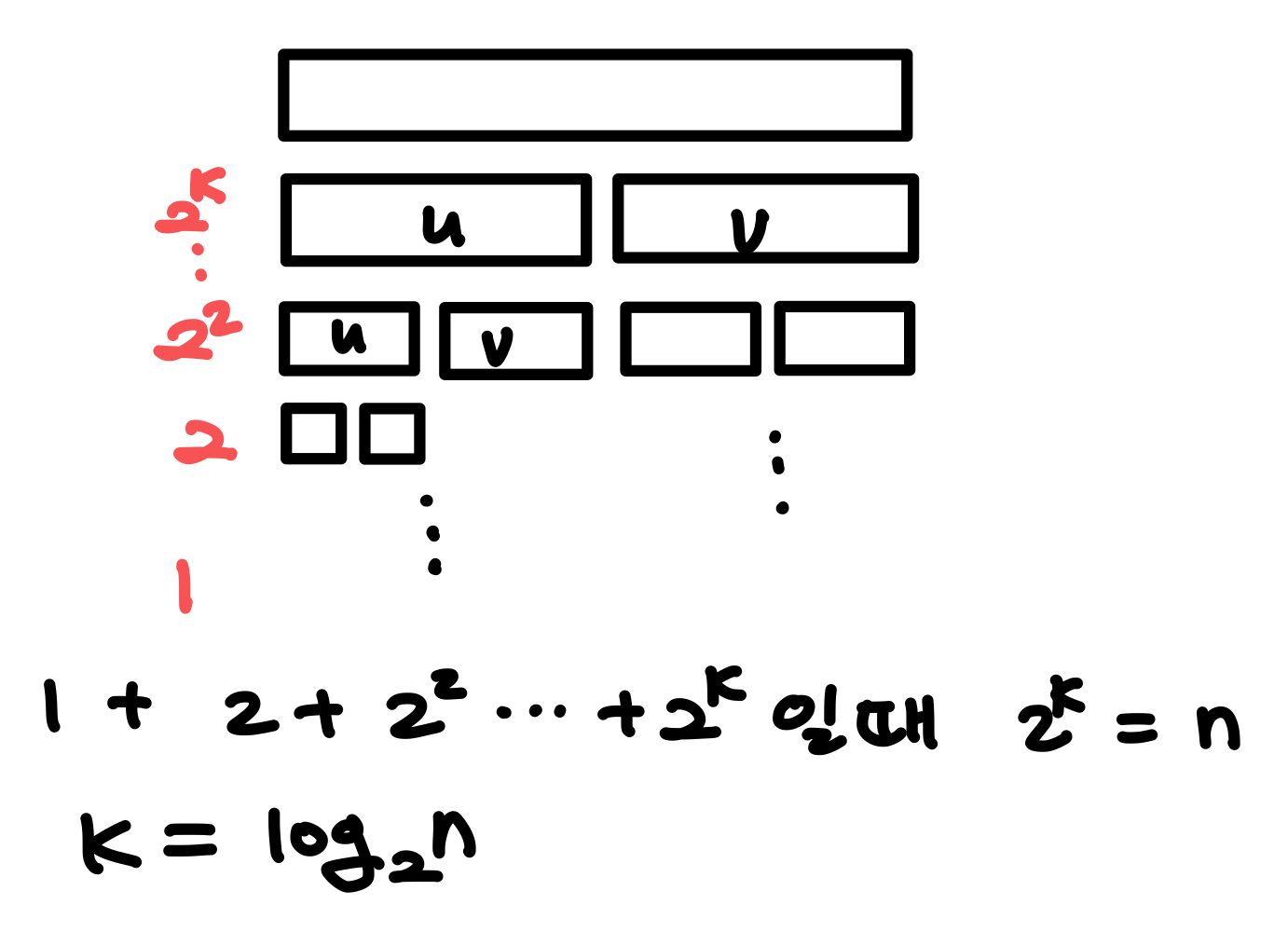
merge sort 공간 복잡도 :

합병 정렬은 기존 배열에서 쪼개서 새 배열 공간 u,v를 추가로 만들어서 사용한다. 배열을 쪼갤 때마다 재귀호출로 배열이 추가로 필요하다. 초기 공간이 n이라 할때 반씩 줄어든 공간이 필요하므로 공간복잡도는 n이다.

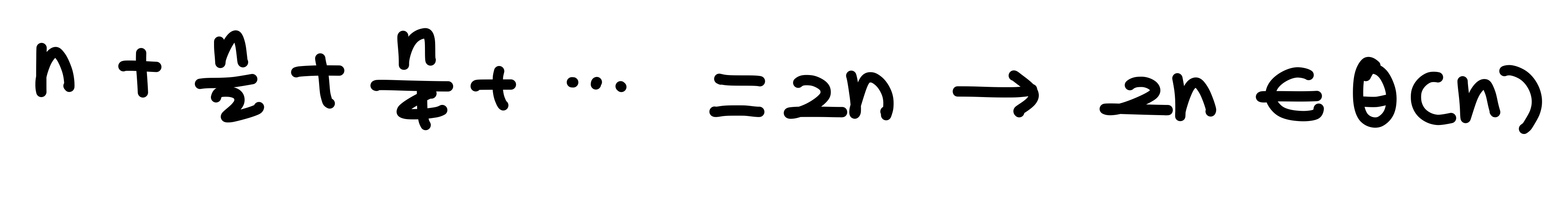
merge sort 시간 복잡도 :

merge sort의 최악의 경우는 A와 B를 끝까지 비교하게 되는 경우, 즉 n개의 자료가 있을 때
n-1번 비교하는 경우이다.

도사정리(Master Theorem)
재귀적인 알고리즘에서 시간복잡도를 계산하지 않고 구할 수 있다.

a와 b를 1보다 큰 상수라고 하고, f(n)을 어떤 함수라 할 때 음수가 아닌 정수 n에 대해 정의된 재현식(반복식) T(n)이 다음과 같은 형태를 이룬다하자.

🎯EX

머지 정렬 방식에 따라 8 5 6 4 2 10 7 1 정렬

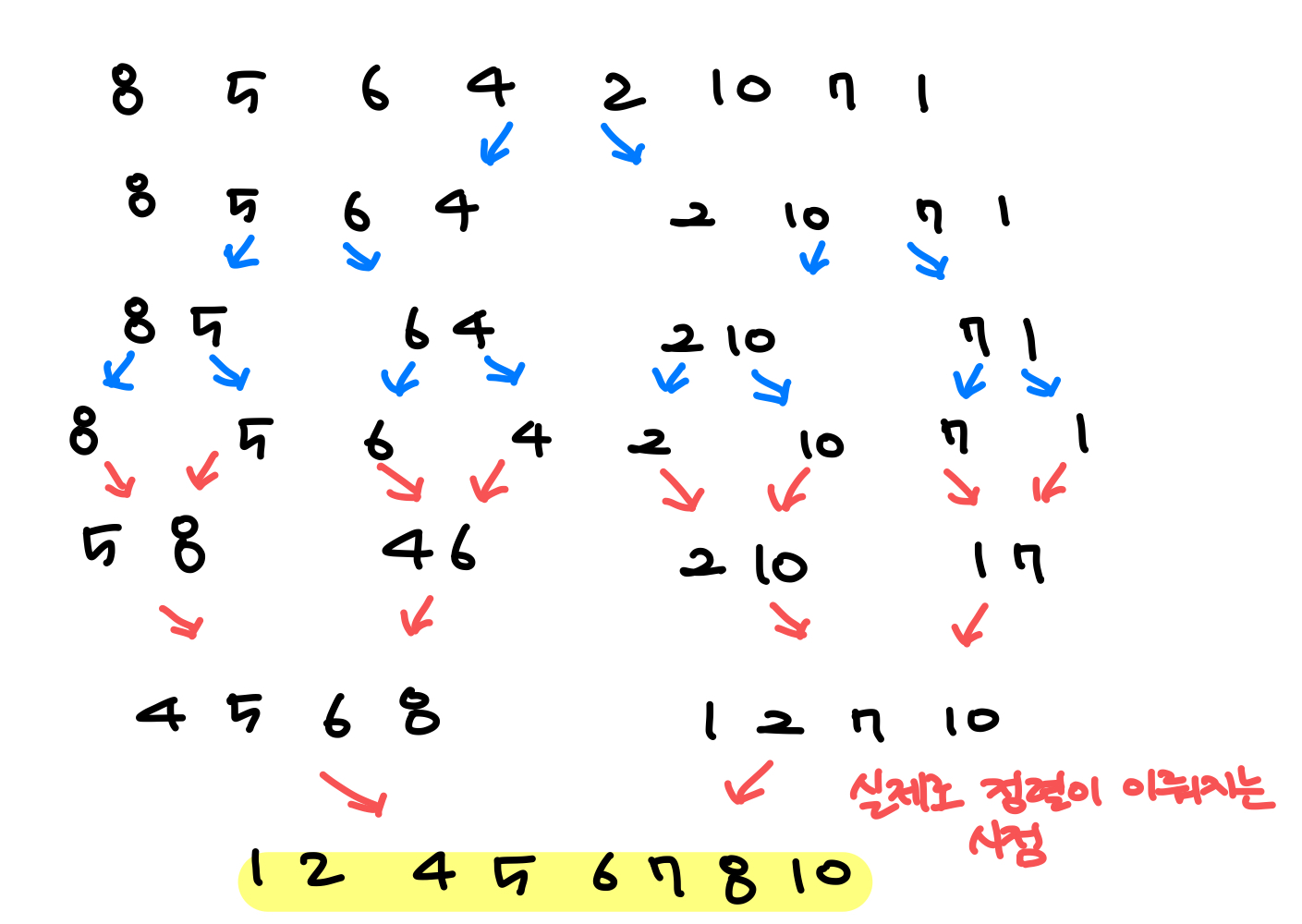배열을 반씩 쪼개서 새 리스트에 저장하고 정렬하며 다시 합친다. divide- and-conqure

구현

#include <iostream>
#include <vector>

using namespace std;
typedef int mytype;
using keytype = int; 

void merge(int h, int m, const keytype U[], const keytype V[], keytype S[]) {
    int i, j, k;
    i = 0; j = 0; k = 0; 
    while (i < h && j < m) {
        if (U[i] < V[j]) {
            S[k] = U[i];
            i++; 
        }
        else {
            S[k] = V[j];
            j++; 
        }
        k++; 
    }
    if (i >= h) // U array의 데이터가 소진되고 V array가 남음
        copy(V + j, V + m, S + k);
    else // V array가 소진 U array가 남음
        copy(U + i, U + h, S + k);
}

void mergeSort(int n, keytype arr[]) {
    if (n > 1) {
        int h = n / 2;
        int m = n - h;
        vector<keytype> U(arr, arr + h);
        vector<keytype> V(arr + h, arr + n);
        
        mergeSort(h, U.data());
        mergeSort(m, V.data());
        
        merge(h, m, U.data(), V.data(), arr);
    }
}

int main() {
	mytype* a;
    cin >> n;

    a = new mytype[n];
    for (int i = 0; i < n; i++) {
        cin >> a[i];
    }
    cout << endl;
    
    mergeSort(n, arr);
    
    cout << "정렬된 배열: ";
    for (int i = 0; i < n; i++) {
        cout << arr[i] << " ";
    }
    cout << endl;
    
    return 0;
}

Heap sort( 힙 정렬)

부모가 자식보다 낫다. 추가 공간 할당 X, 시간복잡도 : O(nlogn)

heap은 완전이진트리(complete binary tree) 구조로 heap이 되기 위한 조건은 다음과 같다.

1. essentially complete binary tree 구조이다.
   min heap의 경우 각 노드에 저장된 값은 자신의 자식 노드들에 저장된 값보다 작거나 같다.
   🌟 root 노드에 저장된 값이 가장 작은 값(min heap)
2. 설계된 힙의 속성에 따라 항상 부모가 자식보다 나은 값을 가진다.
   

• 힙 정렬을 사용해 배열을 정렬할 때는 자기 자신과 자신의 자식 2개만 고려한다.
• 힙은 essentially binary tree 구조이기 때문에 보통 linked list로 구현하는 다른 트리와 달리 배열 기반 인덱싱으로 표현이 가능하다.
  -> 새 노드를 힙의 맨 마지막 위치에 추가해야하는데 이 때 array 기반으로 구현해야 이 과정이 수월하기 때문

구현의 편의를 위해 0번 인덱스는 사용하지 않는다.
완전 이진 트리의 특성을 활용해 array의 index만으로 부모 자식 관계를 정의
n 번 째 노드의 left child node = 2n
n 번 째 노드의 right child node = 2n +1
n 번 째 노드의 parent node = n/2

s[1]	s[2]	s[3]	s[2n]	s[2n+1]
root 노드	root의 자식	s[2]의 자식	s[n]의 왼쪽 자식	s[n]의 오른쪽 자식

heap 정렬이 유용한 경우:

힙 정렬이 가장 유용한 경우는 전체 자료를 정렬하는 것이 아니라 가장 큰 값 몇개만 필요할 때 이다.(특정 조건에 맞는 자료 찾기)

🎯EX

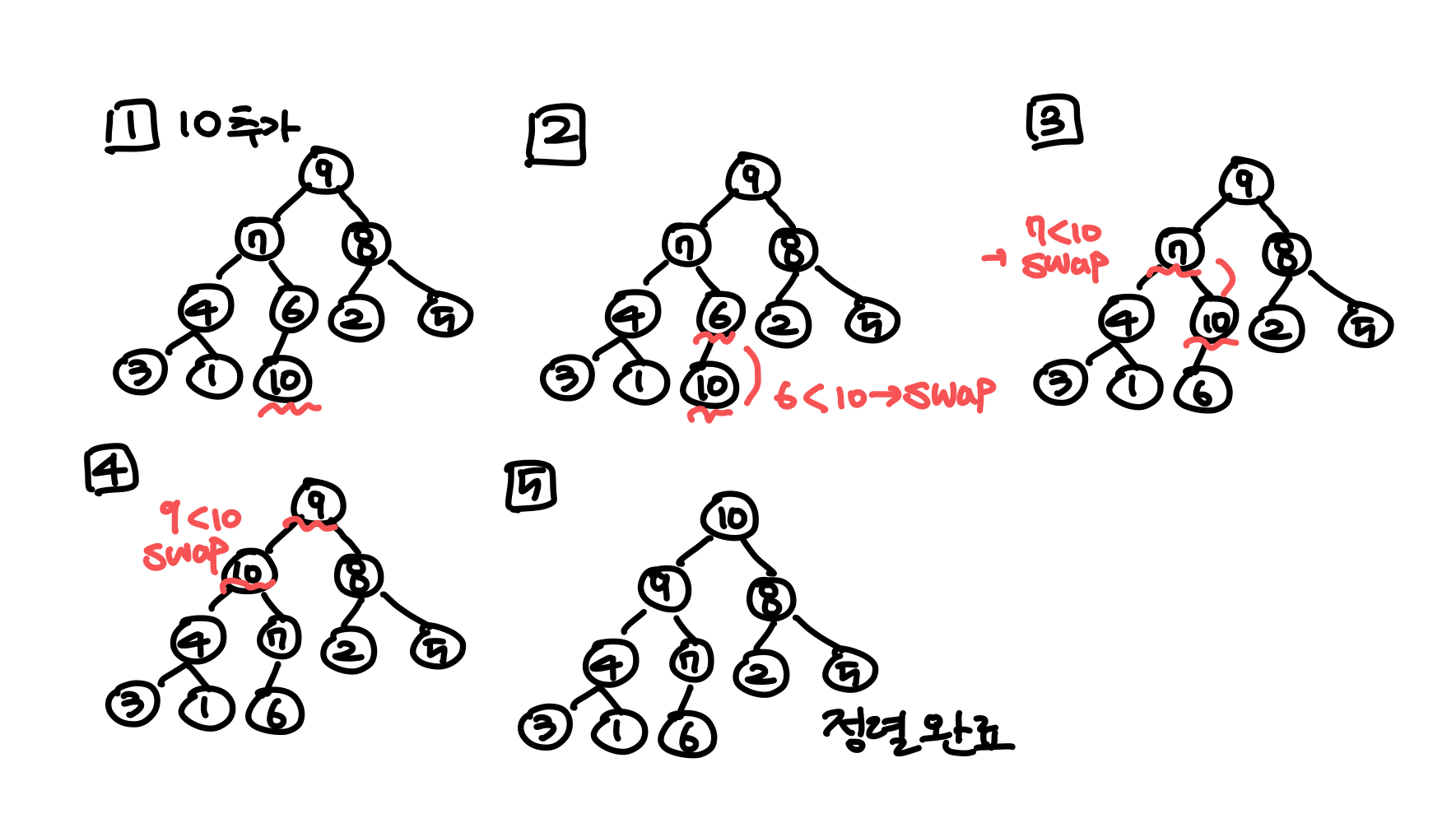
Max heap 데이터 삽입

새로 추가된 데이터는 힙의 가장 마지막 노드에 이어서 들어간다. 새로운 노드들을 부모와 비교해가면서 힙의 조건을 만족시킨다.

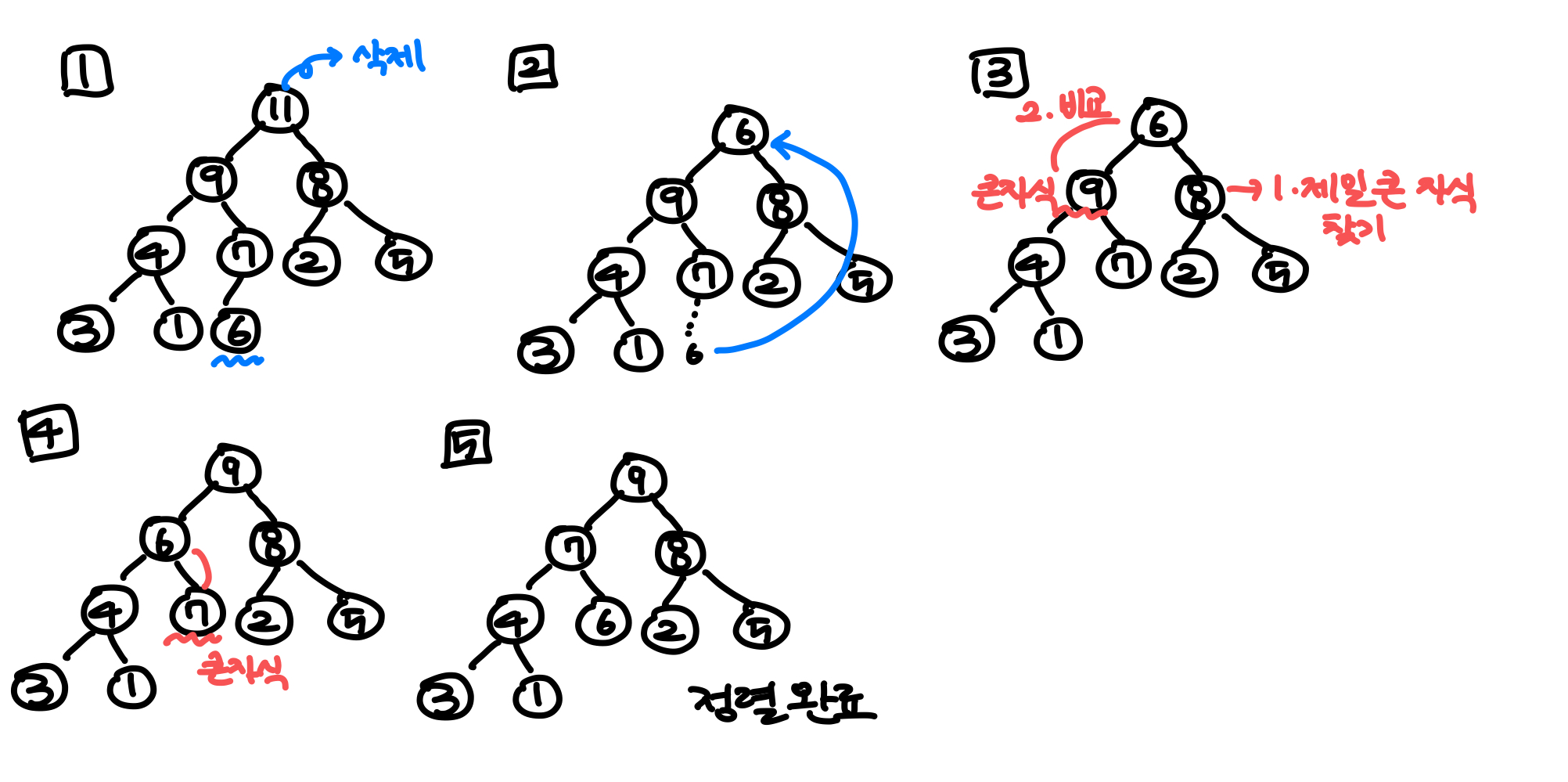
Max heap 데이터 삭제

max heap에서 삭제 연산은 최댓값을 가진 요소를 삭제하는 것이다.maxheap에서 최대값은 루트 노드이므로 루트 노드가 삭제된다.삭제된 루트 노드에는 힙의 마지막 노드를 가져와서 대체하고 힙을 재구성한다.

구현

#include <iostream>
#include <vector>

using namespace std;

struct Node {
    int key;
    Node(int k) : key(k) {}
};

struct Heap {
    vector<Node> nodes;
};

void siftdown(Heap& H) {
    int parentIndex = 0;
    int largerChildIndex = 2 * parentIndex + 1; // 왼쪽 자식

    while (largerChildIndex < H.nodes.size()) {
        if (largerChildIndex + 1 < H.nodes.size() && H.nodes[largerChildIndex + 1].key > H.nodes[largerChildIndex].key) {
            largerChildIndex++; // 오른쪽 자식이 더 큰 경우
        }
        
        if (H.nodes[parentIndex].key >= H.nodes[largerChildIndex].key) {
            break; // 부모가 자식보다 크거나 같으면 종료
        }

        swap(H.nodes[parentIndex], H.nodes[largerChildIndex]);
        parentIndex = largerChildIndex;
        largerChildIndex = 2 * parentIndex + 1;
    }
}

int root(Heap& H) {
    int keyout = H.nodes[0].key;
    H.nodes[0] = H.nodes.back(); // 맨 끝에 추가된 노드를 루트 노드로 이동
    H.nodes.pop_back();
    siftdown(H);
    return keyout;
}

void removeKeys(int n, Heap& H, int S[]) {
    for (int i = n - 1; i >= 0; i--) {
        S[i] = root(H);
    }
}

void makeHeap(int n, Heap& H) {
    for (int i = n / 2 - 1; i >= 0; i--) {
        siftdown(H);
    }
}

void heapSort(int n, Heap& H, int S[]) {
    makeHeap(n, H);
    removeKeys(n, H, S);
}

int main() {

    Heap H;
    for (int i = 0; i < n; i++) {
        H.nodes.push_back(Node(arr[i]));
    }

    int sorted[n];
    heapSort(n, H, sorted);

    cout << "Sorted array: ";
    for (int i = 0; i < n; i++) {
        cout << sorted[i] << " ";
    }
    cout << endl;

    return 0;
}