결측치 처리
1. 결측치 탐색
📌 1. 결측치
- 데이터의 값이 누락된 것 = missing value
- NA, N/A(Not Applicable or Not Available), NaN(Not a Number), Null로 표기
- 설문조사, 종단연구(longtitudinal research)에서 보편적으로 발생
- 설문조사는 참가자 중 일부가 답변하기 곤란한 질문에 의도적으로 응답을 회피할 경우
- 종단연구는 사망, 임의탈퇴, 연락두절 등의 상태인 경우
📌 2. 결측치의 유형
1. MCAR(Missing Completely At Random, 완전 무작위 결측)
- 결측치가 발생한 변수의 값에 상관없이 전체ㅔ 걸쳐 무작위로 발생한 경우
- 통계적으로 결측치의 영향이 없으므로 제거 가능
- ex) 전산오류, 통신문제 등으로 인한 데이터 누락
2. MAR(Missing At Random, 무작위 결측)
- 결측치가 발생한 변수의 값이 다른 변수와 상관관계가 있어 추정이 가능한 경우
- 통계적으로 결측치의 영향이 다소 있으나 편향은 없으므로 대체 가능
- ex) 성별을 사용해 체중을 예측할 경우 여성의 데이터가 누락된 것은 성별에 영향을 받는다
3. MNAR(Missing Not At Random, 비무작위 결측)
- 결측치가 발생한 변수의 값과 관계가 있고 그 이유가 있는 경우
- 통계적으로 결측치의 영향이 크므로 결측치의 원인에 대한 조사 후 대응 필요
- ex) IQ 측정할 경우 105 이하의 IQ에서만 결측치가 나타날 경우
📌 3. 결측치 탐색
1. pandas를 이용한 결측치 탐색
- 데이터 다운로드하기
데이터 다운로드
import pandas as pd
#데이터셋 불러오기
df = pd.read_csv("C:/Users/isabe/Downloads/preprocessing_students.csv", sep = ',')
print(df.head()) id name sex height weight IQ mid_score final_score employed
0 1 홍길동 male 173 62.0 109.0 68.0 78 대기업
1 2 김홍익 female 165 53.0 NaN 91.0 82 공기업
2 3 오나라 female 173 NaN 121.0 NaN 55 창업
3 4 이실장 male 178 78.0 107.0 NaN 56 미취업
4 5 차도남 male 165 82.0 125.0 78.0 74 공기업- 결측치 개수 확인하기
: df.info(), df.isnull(), df.notnull(), .sum(0), .sum(1)
print(df.info())<class 'pandas.core.frame.DataFrame'>
RangeIndex: 20 entries, 0 to 19
Data columns (total 9 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 id 20 non-null int64
1 name 20 non-null object
2 sex 20 non-null object
3 height 20 non-null int64
4 weight 16 non-null float64
5 IQ 14 non-null float64
6 mid_score 14 non-null float64
7 final_score 20 non-null int64
8 employed 18 non-null object
dtypes: float64(3), int64(3), object(3)
memory usage: 1.5+ KB#isnull()의 true 개수 합해서 확인하기
print(df.isnull().sum(axis = 0)) #axis = 0: 열기준 , 1 : 행기준id 0
name 0
sex 0
height 0
weight 4
IQ 6
mid_score 6
final_score 0
employed 2
dtype: int642. klib을 이용해 결측치 탐색
import klib
import warnings
warnings.filterwarnings(action = 'ignore')
#결측치 프로파일링 플롯
print(klib.missingval_plot(df))
#결측치에 대한 프로파일링 플롯
print(klib.missingval_plot(df, sort = True))
#상관관계 플롯
print(klib.corr_plot(df))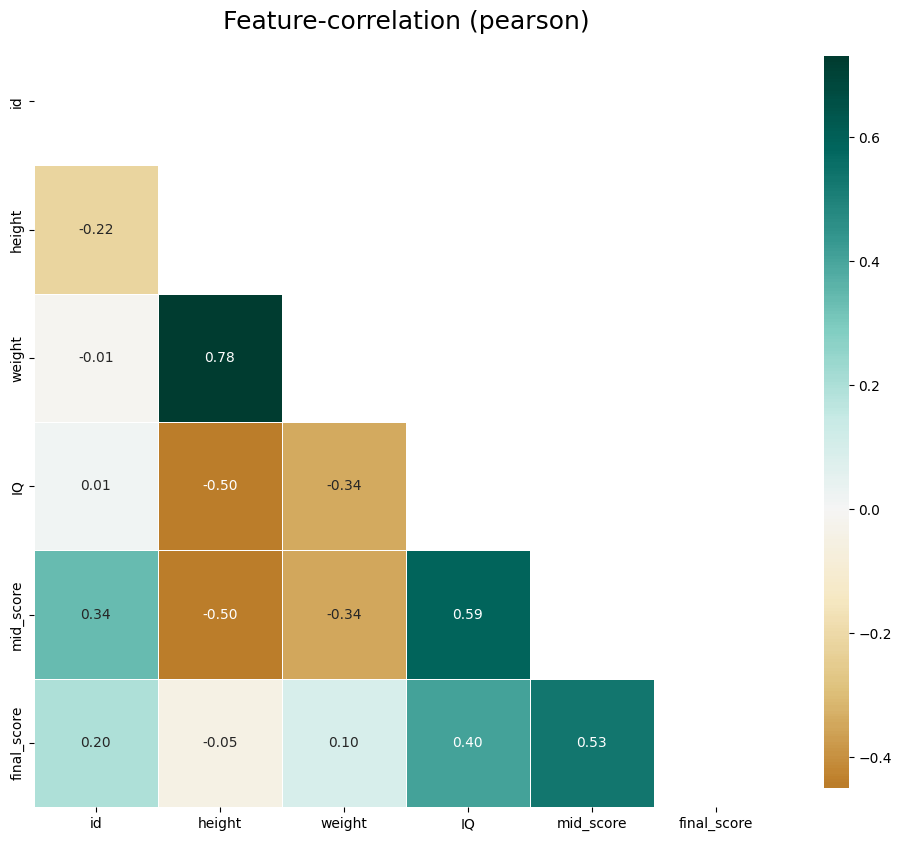
weight와 height가 강한 양의 상관관계(0.78)를 보인다.
IQ와 mid_score가 양의 상관관계(0.59), mid_score와 final_score가 양의 상관관계(0.53)을 보인다.
import matplotlib.pyplot as plt
plt.rc('font', family = 'Malgun Gothic')
#범주형 변수에 대한 분석
print(klib.cat_plot(df))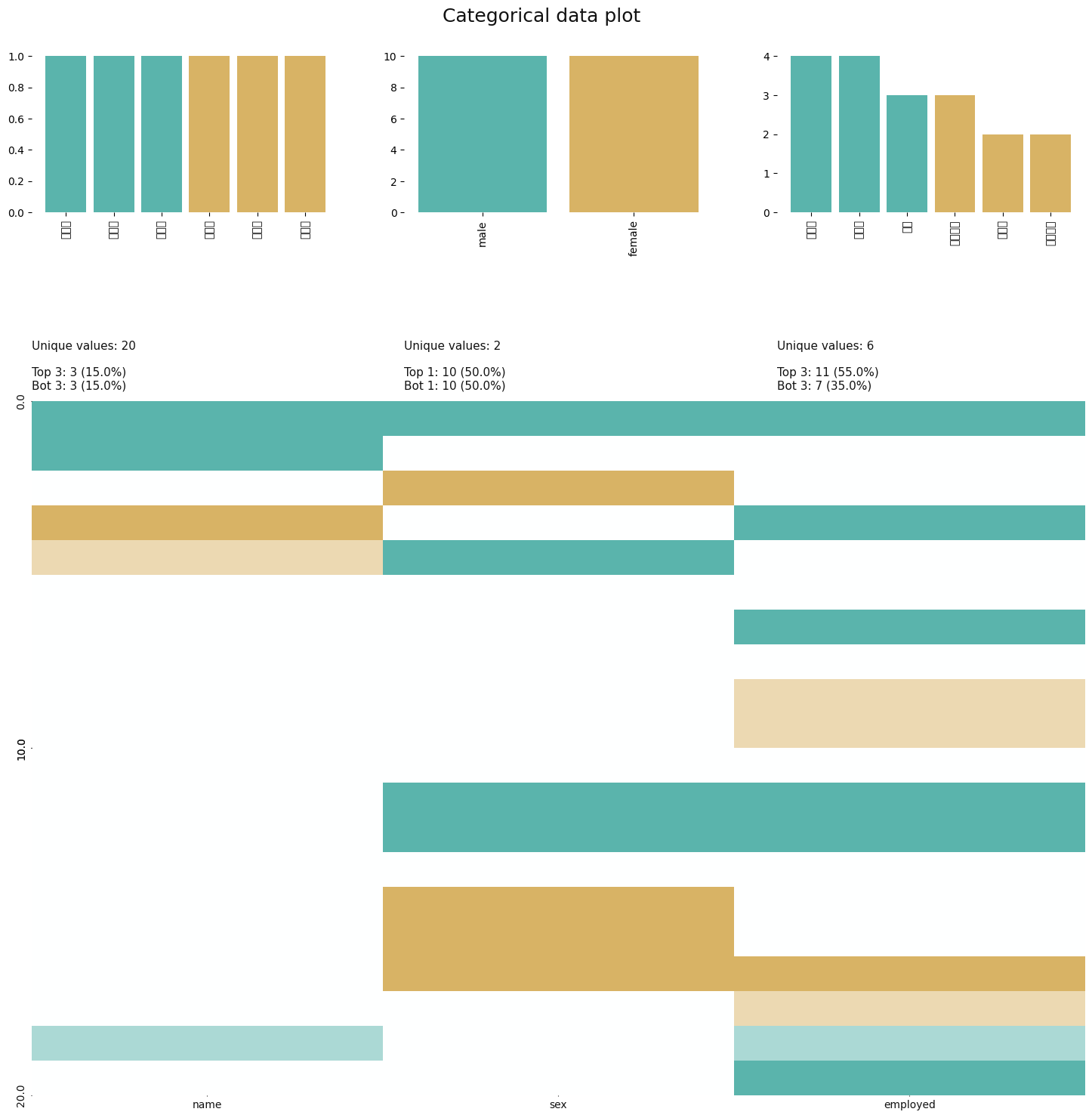
#결측치가 있는 변수의 분표 확인하기
print(klib.dist_plot(df.weight))
print(klib.dist_plot(df.IQ))
print(klib.dist_plot(df.mid_score))
특정한 패턴이 보이지 않음

중간 영역대의 밀도가 낮은 것으로 보아 중간 영역대의 데이터가 누락되었음

낮은 점수대의 데이터가 누락되었음
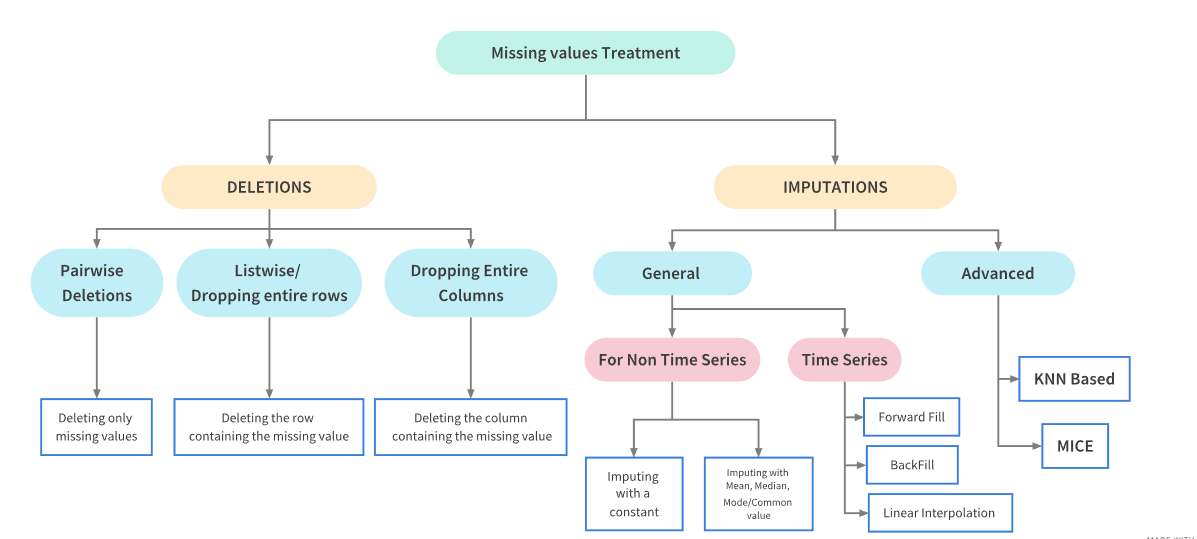
2. 결측치 처리
📌 1. 결측치 처리 개요
-
결측치의 비율에 따른 처리 방법
10% 미만 : 제거 또는 치환
10% 이상 20% 미만 : 모델 기반 처리
20% 이상 : 모델 기반 처리 -
제거(deletion)
: MCAR(완전 무작위 결측)일 때 사용 가능
: 데이터의 손실이 발생 -> 자유도 감소 -> 통계적 검정력 저하
: 표본의 수가 충분하고 결측값이 10-15% 이내일 때에는 결측값을 제거한 후 분석해도 결과에 크게 영향을 주지 않음 -
대체(imputation)
: 표본 평균과 같은 대표값으로 대체할 경우 -> 대표값 데이터가 많아짐 -> 잔차 변동이 줄어듬 -> 잘못된 통계적 결론 유도
: 모수 추정 시 편향(bias) 발생 -
모델 기반 처리
: 결측치를 예측하는 새로운 모델을 구성하고 이를 기반으로 결측치 채워나가는 방식
: 변수의 특성에 따라 Knn, PolyRegression 등 시행 가능
: R 프로그램 패키지인 Mice 함수 사용 가능
📌 2. 결측치 제거(deletion)
- listwise deletion
- 결측치가 존재하는 행(instance) 자체를 삭제
- MCAR일 때만 가능
- 데이터 표본의 숫자가 적은 경우 표본의 축소로 인한 검정력 감소
- pairwise deletion
- 분석에 사용하는 속성의 결측치가 포함된 행만 제거
- MCAR일 때만 가능
import pandas as pd
#listwise deletion
df_listwise = df.dropna()
#pairwise deletion
df_pairwise = df.dropna(subset = ['weight', 'mid_score'])
print(f'original data:\n {df}\n')
print(f'Listwise Deletion:\n {df_listwise}\n')
print(f'Pairwise Deletion:\n {df_pairwise}\n')original data:
id name sex height weight IQ mid_score final_score employed
0 1 홍길동 male 173 62.0 109.0 68.0 78 대기업
1 2 김홍익 female 165 53.0 NaN 91.0 82 공기업
2 3 오나라 female 173 NaN 121.0 NaN 55 창업
3 4 이실장 male 178 78.0 107.0 NaN 56 미취업
4 5 차도남 male 165 82.0 125.0 78.0 74 공기업
5 6 설빛가람 female 154 45.0 132.0 78.0 82 대기업
6 7 김철수 male 187 NaN NaN 63.0 65 미취업
7 8 이영희 female 163 61.0 128.0 74.0 89 중소기업
8 9 김용식 male 167 52.0 NaN 79.0 95 NaN
9 10 풍다희 female 162 56.0 NaN NaN 35 중견기업
10 11 최창현 male 175 61.0 NaN NaN 62 대기업
11 12 남궁선웅 male 176 73.0 108.0 87.0 87 창업
12 13 봉문혁 male 185 97.0 100.0 47.0 67 미취업
13 14 정윤혜 female 158 44.0 103.0 NaN 55 중소기업
14 15 오수경 female 169 55.0 120.0 88.0 65 미취업
15 16 노보선 female 172 89.0 121.0 98.0 94 중견기업
16 17 복하민 female 157 NaN NaN NaN 62 중소기업
17 18 한동진 male 156 42.0 125.0 89.0 73 NaN
18 19 고유진 female 165 NaN 104.0 76.0 89 대기업
19 20 풍진태 male 169 63.0 134.0 98.0 98 창업
Listwise Deletion:
id name sex height weight IQ mid_score final_score employed
0 1 홍길동 male 173 62.0 109.0 68.0 78 대기업
4 5 차도남 male 165 82.0 125.0 78.0 74 공기업
5 6 설빛가람 female 154 45.0 132.0 78.0 82 대기업
7 8 이영희 female 163 61.0 128.0 74.0 89 중소기업
11 12 남궁선웅 male 176 73.0 108.0 87.0 87 창업
12 13 봉문혁 male 185 97.0 100.0 47.0 67 미취업
14 15 오수경 female 169 55.0 120.0 88.0 65 미취업
15 16 노보선 female 172 89.0 121.0 98.0 94 중견기업
19 20 풍진태 male 169 63.0 134.0 98.0 98 창업
Pairwise Deletion:
id name sex height weight IQ mid_score final_score employed
0 1 홍길동 male 173 62.0 109.0 68.0 78 대기업
1 2 김홍익 female 165 53.0 NaN 91.0 82 공기업
4 5 차도남 male 165 82.0 125.0 78.0 74 공기업
5 6 설빛가람 female 154 45.0 132.0 78.0 82 대기업
7 8 이영희 female 163 61.0 128.0 74.0 89 중소기업
8 9 김용식 male 167 52.0 NaN 79.0 95 NaN
11 12 남궁선웅 male 176 73.0 108.0 87.0 87 창업
12 13 봉문혁 male 185 97.0 100.0 47.0 67 미취업
14 15 오수경 female 169 55.0 120.0 88.0 65 미취업
15 16 노보선 female 172 89.0 121.0 98.0 94 중견기업
17 18 한동진 male 156 42.0 125.0 89.0 73 NaN
19 20 풍진태 male 169 63.0 134.0 98.0 98 창업📌 3. 결측치 대체(imputation)
1. 단순대체법(single imputation)
-
결측치의 대체값으로 하나의 값 선정
-
mean, correlation, 회귀계수와 같은 파라미터 추정 시 편향 발생 가능성 높다.
-
추정 편향으로 인해 결측치 제거하는 것보다 통계적 특성이 나빠질 수 있다.
-
종류
- Explicit Modeling
- Mean Imputation
: 데이터의 평균값(mean, median, mode)으로 결측값 대체)
: 평균 대체 -> 표본오차 왜곡, 축소 -> 부정확한 p-value -> 검정력 약화 - Regression imputation
: 회귀식을 만들어 예측된 값으로 결측값 대체
: 관측된 데이터로 1차 회귀식(Linear Regression)선을 구하고 결측치를 회귀선의 y값으로 대체
: 회귀 예측값 대체 -> 잔차 축소, 왜곡 -> R^2 증가, 왜곡 - Stochastic regression imputation
: 회귀 예측값으로 대체하는 것과 유사하지만 random error term을 추가해 예측값에 변동을 주는 방법
: 관측된 값들의 평균과 표준편차 등을 계산하고 확률 모형의 무작위 결과를 통해 결측값 대체
: 표본오차의 과소 추정 문제 있음
- Implicit Modeling
- Hot deck imputation
: 연구중인 자료에서 표본을 바탕으로 비슷한 규칙을 찾아 결측값 대체
: 다른 변수에서 비슷한 값을 갖는 데이터 중 하나를 랜덤 샘플링
: 결측값이 존재하는 변수가 가질 수 있는 값의 범위가 한정되어 있을 때 사용 가능 - Cold deck imputation
: 외부 출처에서 비슷한 연구를 찾아 결측값 대체
: 어떠한 규칙 하(ex. k번째 샘플의 값을 취해온다)에서 하나를 선정
2. 단순대체법 python 적용
- Mean imputation
- scikit-learn의 SimpleImputer 클래스 사용
: strategy : mean/ mode/ most_frequent
: 데이터가 실수 연속값인 경우 평균/ 중앙값 이용, 값의 분포가 대칭적이면 평균, 값의 분포가 심하게 비대칭인 경우 중앙값 사용
: 데이터가 범주값이거나 정수값인 경우 최빈값 사용
- scikit-learn의 SimpleImputer 클래스 사용
- Regression/Stochastic regression imputation
- scikit-learn의 LinearRegression 사용
- Hot deck/ Cold deck imputation
- pandas의 fillna() 사용
from sklearn.impute import SimpleImputer
df_imputed = pd.DataFrame.copy(df)
#110대가 결측인 IQ는 mean으로 대체
df_imputed[['IQ']] = SimpleImputer(strategy = 'mean').fit_transform(df[['IQ']])
#비대칭 분포를 갖는 mid_score은 median으로 대체
df_imputed[['mid_score']] = SimpleImputer(strategy = 'median').fit_transform(df[['mid_score']])
#범주형 employed는 Hot Deck로 대체
df_imputed['employed'].fillna(method = 'bfill', inplace = True)
# height와 양의 상관관계가 있는 weight는 Stochastic regression으로 대체
from sklearn.linear_model import LinearRegression
import numpy as np
# 결측치가 있는 인덱스 검색
idx = df.weight.isnull() == True
# 학습을 위한 데이터 세트 분리
X_train, X_test, y_train = df[['height']][~idx], df[['height']][idx], df[['weight']][~idx]
# 선형회귀모형 인스탄스 생성 후 학습
lm = LinearRegression().fit(X_train, y_train)
# 예측값 + 변동값하여 결측치를 대체
df_imputed.loc[idx, 'weight'] = lm.predict(X_test) + 5*np.random.rand(4,1)
print(df_imputed) id name sex height weight IQ mid_score final_score \
0 1 홍길동 male 173 62.000000 109.000000 68.0 78
1 2 김홍익 female 165 53.000000 116.928571 91.0 82
2 3 오나라 female 173 71.145130 121.000000 78.5 55
3 4 이실장 male 178 78.000000 107.000000 78.5 56
4 5 차도남 male 165 82.000000 125.000000 78.0 74
5 6 설빛가람 female 154 45.000000 132.000000 78.0 82
6 7 김철수 male 187 93.305695 116.928571 63.0 65
7 8 이영희 female 163 61.000000 128.000000 74.0 89
8 9 김용식 male 167 52.000000 116.928571 79.0 95
9 10 풍다희 female 162 56.000000 116.928571 78.5 35
10 11 최창현 male 175 61.000000 116.928571 78.5 62
11 12 남궁선웅 male 176 73.000000 108.000000 87.0 87
12 13 봉문혁 male 185 97.000000 100.000000 47.0 67
13 14 정윤혜 female 158 44.000000 103.000000 78.5 55
14 15 오수경 female 169 55.000000 120.000000 88.0 65
15 16 노보선 female 172 89.000000 121.000000 98.0 94
16 17 복하민 female 157 49.637373 116.928571 78.5 62
17 18 한동진 male 156 42.000000 125.000000 89.0 73
18 19 고유진 female 165 59.299214 104.000000 76.0 89
19 20 풍진태 male 169 63.000000 134.000000 98.0 98
employed
0 대기업
1 공기업
2 창업
3 미취업
4 공기업
5 대기업
6 미취업
7 중소기업
8 중견기업
9 중견기업
10 대기업
11 창업
12 미취업
13 중소기업
14 미취업
15 중견기업
16 중소기업
17 대기업
18 대기업
19 창업 3. 다중대체법(Multiple Imputation)
- 결측치의 대체값을 여러 추정값을 종합해 선정하는 것
- 단일대체법의 문제점인 표준오차의 과소추정을 보완한 방법
- 다중대체법의 3단계
1. imputation phase : 가능한 대체값의 분포에서 추출된 서로 다른 값으로 복수의 데이터셋 생성- analysis phase : 각 데이터셋에 대해 모수의 추정치와 표본오차 계산
- pooling phase : 모든 데이터셋의 추정치와 표본오차를 통합하여 하나의 대치값 생성
- 종류 : 사전 분포 가정의 존재 여부에 따라 MVNI, MICE로
MVNI(Multivariate normal imputation)은 다변량 정규분포 대체방식으로 MCMC(Markov Chain Monte Carlo)가 대표적인 예시이며, MICE(Multiple Implutation with Chained Equations)는 연쇄방정식에 의한 다중대체로 이외에도 딥러닝을 활용한 GAIN(Generative adversarial imputation nets) 등이 있다.
- MICE(Multivariate Imputation by Chained Equation)
- 누락된 데이터를 여러번 채우는 방식, 여러 결측치 대치 세트를 만들어 with함수로 특정 통계 모델링을 수행하고 pool함수로 생성한 m개의 대치세트를 평균하여 결과 도출. 연속형, 이진형, 범위형 패턴도 처리 가능
import numpy as np
from sklearn.experimental import enable_iterative_imputer
from sklearn.impute import IterativeImputer
# 데이터 세트
X_train = [[33, np.nan, .153], [18, 12000, np.nan], [np.nan, 13542, .125]]
X_test = [[45, 10300, np.nan], [np.nan, 13430, .273], [15, np.nan, .165]]
# mice 인스턴스 생성
mice = IterativeImputer(max_iter=10, random_state=0)
mice.fit(X_train)
np.set_printoptions(precision=5, suppress=True)
print('X_train MICE: \n', mice.transform(X_train))
print('X_test MICE: \n', mice.transform(X_test))X_train MICE:
[[ 33. 12770.99952 0.153 ]
[ 18. 12000. 0.181 ]
[ 48.00002 13542. 0.125 ]]
X_test MICE:
[[ 45. 10300. 0.2427 ]
[ 45.82103 13430. 0.273 ]
[ 15. 11845.80217 0.165 ]]- KNN imputation
- KNN(K-Nearest Neighbor)은 분석대상을 중심으로 가장 가까운 k개 요소들 중에서 가장 많은 수의 집단으로 분류하는 지도학습 알고리즘
- KNN imputation은 결측치가 범주형이면 이웃 데이터 중 최빈값으로 대체하고 연속형이면 이웃 데이터들의 중앙값으로 대체
- but 이상치에 민감하다는 단점 존재
import numpy as np
from sklearn.impute import KNNImputer
knn = KNNImputer(n_neighbors=2, weights="uniform")
knn.fit(X_train)
print('X_train KNN: \n', knn.transform(X_train))
print('X_test KNN: \n', knn.transform(X_test))X_train KNN:
[[ 33. 12771. 0.153]
[ 18. 12000. 0.139]
[ 25.5 13542. 0.125]]
X_test KNN:
[[ 45. 10300. 0.139]
[ 25.5 13430. 0.273]
[ 15. 12771. 0.165]]