노이즈 처리
1. 노이즈(Noise)
📌 1. 노이즈
- 측정된 변수에 무작위의 오류(random error)또는 분산으로 존재하는 것
1. 정형 데이터의 노이즈
- 정형 데이터에서 노이즈는 분산(variance)으로 나타남
- 통계 모형에서는 오차항으로 나타남
ex) 단순선형회귀모형에서 오차항 ϵ이 노이즈
2. 이미지/영상 데이터의 노이즈
- blur : 이미지가 흐릿하게 보이는 현상
- white noise : 백색 잡음, 모든 주파수를 가진 잡음
- pink noise : 특정 주파수 대역(일반적으로 낮은 주파수)에서 강하게 나오는 노이즈
- Gaussian noise : 가우시안 분포를 따르는 노이즈
3. 시계열/음성/신호 데이터의 노이즈
- 일반적으로 white noise, Gaussian noise으로 나타남
- white noise는 모든 주파수 영역에서 동일한 에너지를 가지는 잡음
- Gaussian noise는 평균이 0이고 분산이 1인 정규분포를 따르는 잡음
4. 텍스트 데이터의 노이즈
- 일반적으로 철자 오류, 약어, 비표준 단어, 반복, 구두점 누락, 의성어 등
- 텍스트 데이터의 노이즈는 자연어 처리의 성능을 저하시키는 중요한 요인
- 자동 음성 인식, 광학 문자 인식, 기계 번역, Web Scraping 등으로 수집한 데이터에 노이즈가 많음
📌 2. Defact / Fault / Artifact / Noise
- Defact(결함)
- 전체 데이터에 존재하는 일부 오류(error)데이터
: 범위에서 벗어난 이상치가 아니라 잘못된 데이터
: 주로 생산, 제조 분야
: Defact가 제품/설비의 기능에 손상을 야기하면 제품/설비가 Fault(불량)이 됨
- Artifact
- Defact와 동일한 의미를 갖는 용어
: 주로 과학기술 분야에서 사용, 주로 이미지의 defact 지칭
- Noise
- 일반적으로 원인을 알 수 없는 무작위 변동 의미
: 주로 신호처리(signal processint) 분야에서 사용
: 동작 기전을 모르므로 제거는 불가하고 이를 저감(denoising)해야 함
2. 디노이징(Denoising)
📌 1. 정형 데이터의 디노이징
1. 구간화(Binning)
-
정렬된 데이터 값들을 몇 개의 bin으로 분할해 대표값으로 대체
-
구간 설정 방법
- 동일 간격(equal-distance) 구간화 : pandas의 cut() 사용
- 동일 빈도(equal-frequency) 구간화 : pandas의 qcut() 사용
-
구간별 대표값 설정 방법
평균값 평활화 : bin에 있는 값들을 평균값으로 대체
중앙값 평활화 : 중앙값으로 대체
경계값 평활화 : 경계값 중 가까운 값으로 대체
import pandas as pd
import numpy as np
#데이터 생성하기
df = pd.DataFrame({'uniform' : np.sort(np.random.uniform(0, 10, 10)),
'normal' : np.sort(np.random.normal(5, 1, 10)),
'gamma' : np.sort(np.random.gamma(2, size = 10))})
#데이터 확인하기
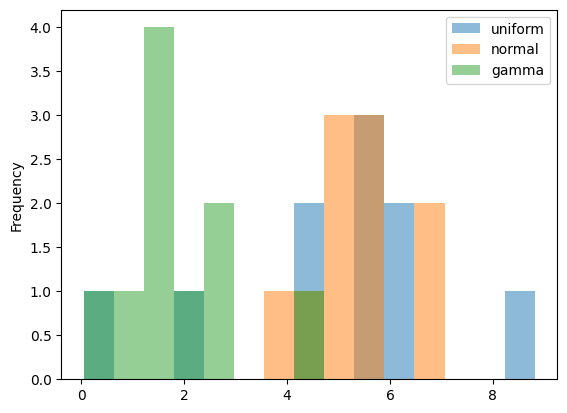
df.plot(kind = 'hist', bins = 15, alpha = 0.5)
df.describe() uniform normal gamma
count 10.000000 10.000000 10.000000
mean 4.973770 5.376446 1.861706
std 2.316884 0.850170 1.180829
min 0.589282 3.830165 0.054764
25% 4.412152 4.929383 1.255541
50% 5.522566 5.377682 1.709675
75% 6.173430 5.628082 2.493288
max 8.812105 6.718039 4.175562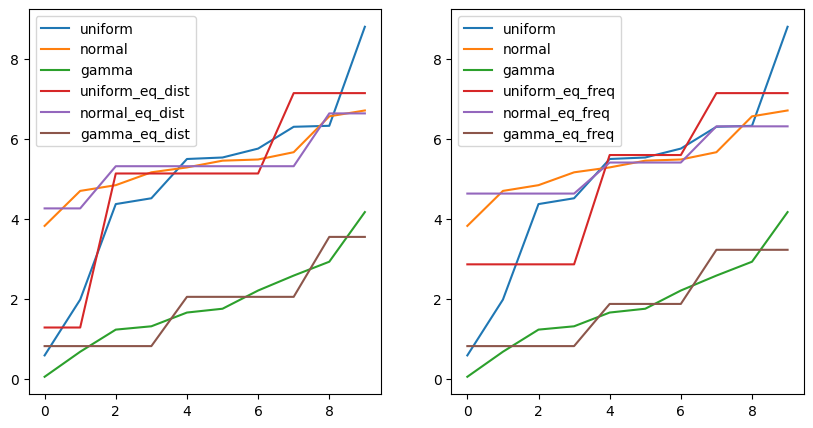
1) pandas로 구간화
- cut() , qcut() 동작 확인
col = 'uniform'
num_bins = 5
df_binned = pd.DataFrame()
#원래 데이터
df_binned[col] = df[col].sort_values()
#동일 간격으로 나누기 : cut()
df_binned['eq_dist_auto'] = pd.cut(df_binned[col], num_bins)
#지정된 구간으로 나누기
df_binned['eq_dist_fixed'] = pd.cut(df_binned[col], bins = [0,2,4,6,8,10])
#동일 빈도로 나누기 : qcut()
df_binned['eq_freq_auto'] = pd.qcut(df_binned[col], num_bins)
df_binned uniform eq_dist_auto eq_dist_fixed eq_freq_auto
0 0.589282 (0.581, 2.234] (0, 2] (0.588, 3.898]
1 1.985700 (0.581, 2.234] (0, 2] (0.588, 3.898]
2 4.375758 (3.878, 5.523] (4, 6] (3.898, 5.111]
3 4.521335 (3.878, 5.523] (4, 6] (3.898, 5.111]
4 5.503819 (3.878, 5.523] (4, 6] (5.111, 5.63]
5 5.541313 (5.523, 7.168] (4, 6] (5.111, 5.63]
6 5.764158 (5.523, 7.168] (4, 6] (5.63, 6.315]
7 6.309853 (5.523, 7.168] (6, 8] (5.63, 6.315]
8 6.334373 (5.523, 7.168] (6, 8] (6.315, 8.812]
9 8.812105 (7.168, 8.812] (8, 10] (6.315, 8.812]- 구간화하여 평균값 대체하기
cols = ['uniform', 'normal', 'gamma']
#동일 간격 구간화
df_eqw = df.copy()
for col in cols :
df_eqw[col + '_eq_dist'] = pd.cut(df_eqw[col], 3) #구간으로 나누기
means = df_eqw.groupby(col + '_eq_dist')[col].mean() #구간별 평균값 계산
df_eqw.replace({col + '_eq_dist' : means}, inplace = True) #평균값 대체
display(df_eqw)
#동일 빈도 구간화
df_eqf = df.copy()
for col in cols :
df_eqf[col + '_eq_freq'] = pd.qcut(df_eqf[col], 3) #구간으로 나누기
means = df_eqf.groupby(col + '_eq_freq')[col].mean() #구간별 평균값 계산
df_eqf.replace({col + '_eq_freq' : means}, inplace = True) #평균값 대체
display(df_eqf)
#시각화
import matplotlib.pyplot as plt
fig, axes = plt.subplots(1, 2, figsize = (10, 5))
df_eqw.astype(float).plot(ax = axes[0])
df_eqf.astype(float).plot(ax = axes[1])
plt.show() uniform normal gamma uniform_eq_dist normal_eq_dist gamma_eq_dist
0 0.589282 3.830165 0.054764 1.287491 4.267738 0.822230
1 1.985700 4.705312 0.681460 1.287491 4.267738 0.822230
2 4.375758 4.848995 1.234735 5.141277 5.323289 0.822230
3 4.521335 5.170547 1.317962 5.141277 5.323289 0.822230
4 5.503819 5.293394 1.661983 5.141277 5.323289 2.054775
5 5.541313 5.461970 1.757367 5.141277 5.323289 2.054775
6 5.764158 5.491075 2.213051 5.141277 5.323289 2.054775
7 6.309853 5.673751 2.586700 7.152110 5.323289 2.054775
8 6.334373 6.571216 2.933474 7.152110 6.644627 3.554518
9 8.812105 6.718039 4.175562 7.152110 6.644627 3.554518
uniform normal gamma uniform_eq_freq normal_eq_freq gamma_eq_freq
0 0.589282 3.830165 0.054764 2.868019 4.638755 0.822230
1 1.985700 4.705312 0.681460 2.868019 4.638755 0.822230
2 4.375758 4.848995 1.234735 2.868019 4.638755 0.822230
3 4.521335 5.170547 1.317962 2.868019 4.638755 0.822230
4 5.503819 5.293394 1.661983 5.603097 5.415480 1.877467
5 5.541313 5.461970 1.757367 5.603097 5.415480 1.877467
6 5.764158 5.491075 2.213051 5.603097 5.415480 1.877467
7 6.309853 5.673751 2.586700 7.152110 6.321002 3.231912
8 6.334373 6.571216 2.933474 7.152110 6.321002 3.231912
9 8.812105 6.718039 4.175562 7.152110 6.321002 3.231912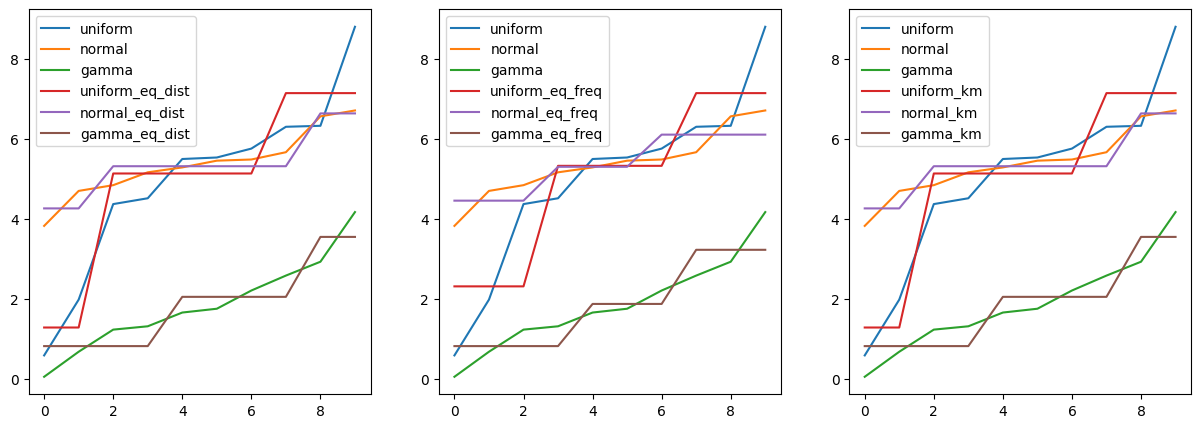
2. 군집화(clustering)
-
scikit-learn으로 구간화
: KBinsDiscretizer() 사용
encode{‘onehot’, ‘onehot-dense’, ‘ordinal’}, default=’onehot’
strategy{‘uniform’(동일간격), ‘quantile’(동일빈도), ‘kmeans’(K-Means 군집화)}, default=’quantile’ -
구간화하기
import warnings
warnings.filterwarnings("ignore")
from sklearn.preprocessing import KBinsDiscretizer
#동일 간격 구간화
ed_binner = KBinsDiscretizer(n_bins = 3, encode = 'ordinal', strategy = 'uniform', subsample = None)
df_ed = ed_binner.fit_transform(df)
#동일 빈도 구간화
ef_binner = KBinsDiscretizer(n_bins = 3, encode = 'ordinal', strategy = 'quantile', subsample = None)
df_ef = ef_binner.fit_transform(df)
#K-Means 구간화
km_binner = KBinsDiscretizer(n_bins = 3, encode = 'ordinal', strategy = 'kmeans', subsample = None)
df_km = km_binner.fit_transform(df)
#결과 확인
df_ed = pd.DataFrame(df_ed, columns = df.columns + '_eq_dist')
df_ef = pd.DataFrame(df_ef, columns = df.columns + '_eq_freq')
df_km = pd.DataFrame(df_km, columns = df.columns + '_km')
df_bin = pd.concat([df, df_ed, df_ef, df_km], axis = 1)
df_bin uniform normal gamma uniform_eq_dist normal_eq_dist gamma_eq_dist uniform_eq_freq normal_eq_freq gamma_eq_freq uniform_km normal_km gamma_km
0 0.589282 3.830165 0.054764 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
1 1.985700 4.705312 0.681460 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
2 4.375758 4.848995 1.234735 1.0 1.0 0.0 0.0 0.0 0.0 1.0 1.0 0.0
3 4.521335 5.170547 1.317962 1.0 1.0 0.0 1.0 1.0 0.0 1.0 1.0 0.0
4 5.503819 5.293394 1.661983 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
5 5.541313 5.461970 1.757367 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
6 5.764158 5.491075 2.213051 1.0 1.0 1.0 1.0 2.0 1.0 1.0 1.0 1.0
7 6.309853 5.673751 2.586700 2.0 1.0 1.0 2.0 2.0 2.0 2.0 1.0 1.0
8 6.334373 6.571216 2.933474 2.0 2.0 2.0 2.0 2.0 2.0 2.0 2.0 2.0
9 8.812105 6.718039 4.175562 2.0 2.0 2.0 2.0 2.0 2.0 2.0 2.0 2.0- 구간화하여 평균값 대체하기
for bin_col in df_bin.columns:
col = bin_col.split('_')[0]
means = df_bin.groupby(by = bin_col)[col].mean()
df_bin.replace({bin_col:means}, inplace = True)
df_bin0 0.589282 3.830165 0.054764 1.287491 4.267738 0.822230 2.316913 4.461491 0.822230 1.287491 4.267738 0.822230
1 1.985700 4.705312 0.681460 1.287491 4.267738 0.822230 2.316913 4.461491 0.822230 1.287491 4.267738 0.822230
2 4.375758 4.848995 1.234735 5.141277 5.323289 0.822230 2.316913 4.461491 0.822230 5.141277 5.323289 0.822230
3 4.521335 5.170547 1.317962 5.141277 5.323289 0.822230 5.332656 5.308637 0.822230 5.141277 5.323289 0.822230
4 5.503819 5.293394 1.661983 5.141277 5.323289 2.054775 5.332656 5.308637 1.877467 5.141277 5.323289 2.054775
5 5.541313 5.461970 1.757367 5.141277 5.323289 2.054775 5.332656 5.308637 1.877467 5.141277 5.323289 2.054775
6 5.764158 5.491075 2.213051 5.141277 5.323289 2.054775 5.332656 6.113520 1.877467 5.141277 5.323289 2.054775
7 6.309853 5.673751 2.586700 7.152110 5.323289 2.054775 7.152110 6.113520 3.231912 7.152110 5.323289 2.054775
8 6.334373 6.571216 2.933474 7.152110 6.644627 3.554518 7.152110 6.113520 3.231912 7.152110 6.644627 3.554518
9 8.812105 6.718039 4.175562 7.152110 6.644627 3.554518 7.152110 6.113520 3.231912 7.152110 6.644627 3.554518- 시각화
import matplotlib.pyplot as plt
fig, axes = plt.subplots(1, 3, figsize = (15, 5))
pd.concat([df_bin.iloc[:, :3], df_bin.iloc[:, 3:6]], axis = 1).astype(float).plot(ax = axes[0])
pd.concat([df_bin.iloc[:, :3], df_bin.iloc[:, 6:9]], axis = 1).astype(float).plot(ax = axes[1])
pd.concat([df_bin.iloc[:, :3], df_bin.iloc[:, 9:]], axis = 1).astype(float).plot(ax = axes[2])
plt.show()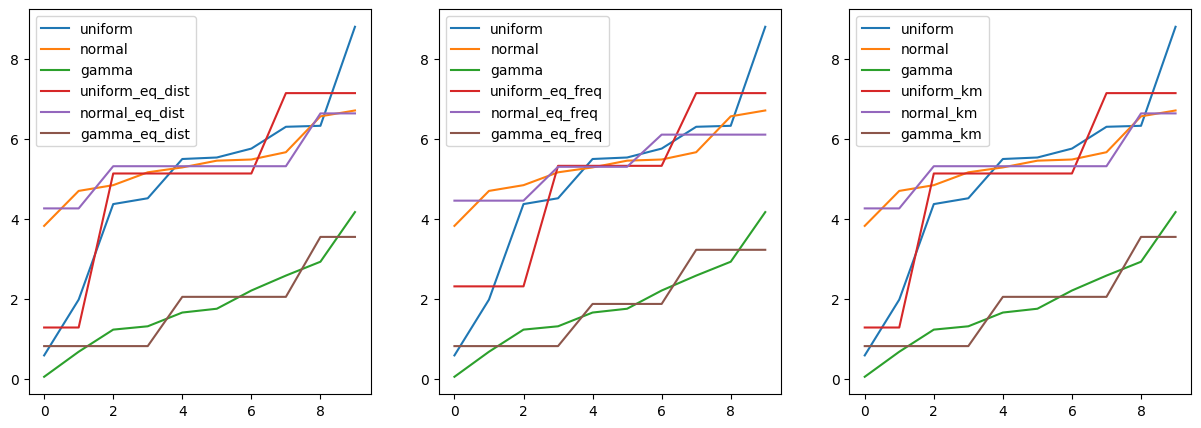
📌 2. 시계열 데이터의 디노이징
- 예시 데이터셋 불러오기
!pip install finanace-datareader- 사용 라이브러리 : finance datareader
한국과 글로벌 거래소에 상장되어있는 주식 종목의 시계열 데이터를 불러올 수 있는 라이브러리 - 삼성 전자의 2021년 전체 시계열 주가 데이터를 불러오기
import pandas as pd
import FinanceDataReader as fdr
import matplotlib.pyplot as plt
start_date = "20210101"
end_date = "20211231"
sample_code = "005930" #삼성전자
df = fdr.DataReader(sample_code, start = start_date, end = end_date)
df Open High Low Close Volume Change
Date
2022-01-03 79400 79800 78200 78600 13502112 0.003831
2022-01-04 78800 79200 78300 78700 12427416 0.001272
2022-01-05 78800 79000 76400 77400 25470640 -0.016518
2022-01-06 76700 77600 76600 76900 12931954 -0.006460
2022-01-07 78100 78400 77400 78300 15163757 0.018205
... ... ... ... ... ... ...
2022-12-23 58200 58400 57700 58100 9829407 -0.016920
2022-12-26 58000 58100 57700 57900 6756411 -0.003442
2022-12-27 58000 58400 57900 58100 10667027 0.003454
2022-12-28 57600 57600 56400 56600 14665410 -0.025818
2022-12-29 56000 56200 55300 55300 11295935 -0.022968
246 rows × 6 columns1. 단순 이동평균법(Simple Moving Average)
: 평균값으로 관측치 대체, 이상치들을 평활화할 수 있다.
: m일의 평균을 구해본다고 가정한다면, n번째 데이터의 단순이동평균 = n번째 데이터를 포함한 왼쪽 m개의 데이터의 산술평균
: window 크기와 m값에 큰 영향을 받는다.
# 단순 이동평균
# 5일 이동평균
ma5 = df['Close'].rolling(window=5).mean()
df['ma5'] = ma5
# 20일
ma20 = df['Close'].rolling(window=20).mean()
df['ma20'] = ma20
# 60일(기업실적 발표 사이클)
ma60 = df['Close'].rolling(window=60).mean()
df['ma60'] = ma60
# 120일(기업 반기결산 사이클)
ma120 = df['Close'].rolling(window=120).mean()
df['ma120'] = ma120- plotting
def draw(df):
plt.figure(figsize=(10, 5))
plt.plot(df.index, df['Close'],label='Close')
plt.plot(df.index, df['ma5'],label='ma5')
plt.plot(df.index, df['ma20'],label='ma20')
plt.plot(df.index, df['ma60'],label='ma60')
plt.plot(df.index, df['ma120'],label='ma120')
plt.legend()
plt.grid(alpha=0.5)
plt.show()
draw(df.loc[start_date:end_date])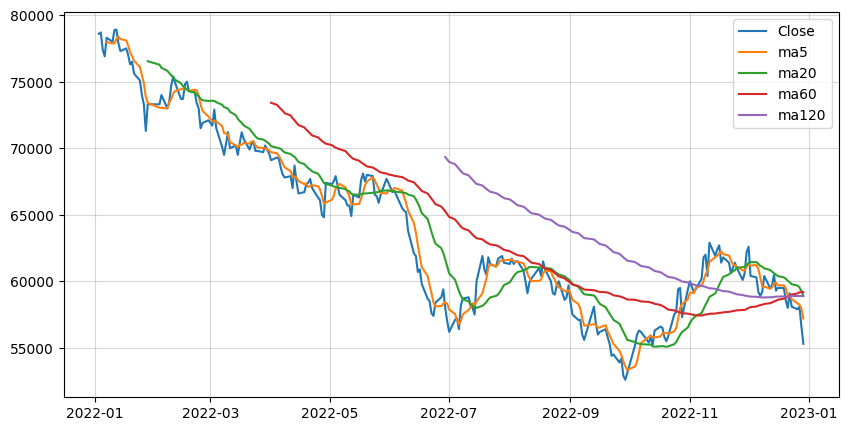
2. 지수이동평균(Exponential Moving Average)
: 최근값에 가중치를 두는 방식
: 가장 오래된 데이터부터 시작해 재귀적으로(recursive)하게 가장 최근 데이터까지 지수 가중 이동평균을 구할 수 있다.
# 12일, 26일에 대한 지수 이동평균
short = 12
long = 26
df["ema_short"] = df["Close"].ewm(short).mean()
df["ema_long"] = df["Close"].ewm(long).mean()# "Close", "ema_short", "ema_long" 시각화
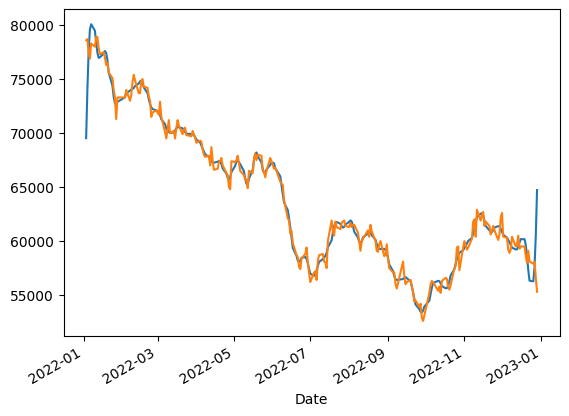
df[["Close", "ema_short", "ema_long"]].plot()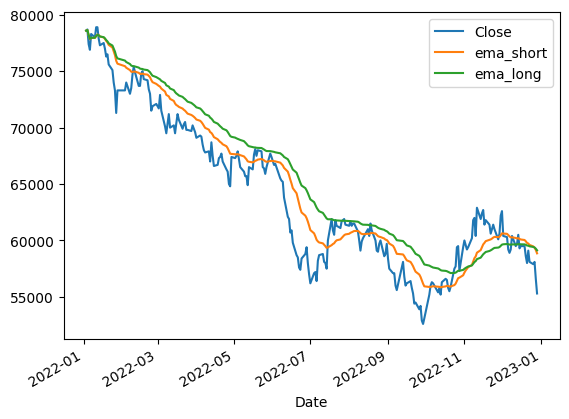
3. 푸리에 변환(Fourier Transform)
어떤 복잡한 파동이라도 진동수와 진폭이 다른 간단한 파동들의 합으로 나타낼 수 있다는 푸리에 정리를 이용해 잡음 제거에 활용하면 시간 차원에서 발생한 주식 종가 가격을 주파수 차원으로 변환하여 특정 상위 파동들의 합(예시에서는 상위 30개)을 계산하고 다시 시간 차원으로 변환한다. 이를 통해 잡음을 제거하여 올바른 신호를 포착할 수 있다.
import numpy as np
def FFT(df, col, topn=2):
fft = np.fft.fft(df[col])
fft[topn:-topn] = 0
ifft = np.fft.ifft(fft)
return ifft
df['FFT(30)'] = FFT(df, 'Close', 30)
df['FFT(30)'].plot() #FFT 플로팅
df['Close'].plot() #Raw데이터 플로팅