[ML/Python] K-최근접 이웃(K-NN) 분류(Classifier) 기법 알고리즘 실습

K-NN(K-Nearest Neighbor) 분류 기법 실습

Python 라이브러리

%matplotlib inline # notebook 환경에서 바로 볼 수 있도록 해줌
import matplotlib.pyplot as plt
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.datasets import load_breast_cancer

• KNeighborsClassifier (sklearn페이지 참고) :
  • n_neighbors : default=5 , 이웃 갯수
  • .fit(X,y) : training dataset 학습
  • .predict(X) : X data에 대한 class labels 예측
  • .score(X, y) : dataset의 평균 정확도 return
• load_breast_cancer : sklearn 유방암 데이터 사용 (load_breast_cancer)
• train_test_split:
  • train_size : default=0.25, train 데이터 셋의 비율
  • test_size : default=0.25, test(validation) 데이터 셋의 비율
  • shuffle : default=True, split해주기 전에 섞을건지 여부. 보통 default값으로 놔둠
  • stratify*: default=None, stratify 값을 target으로 지정하면, 각각의 class 비율을 train / test(validation)에 유지하여, 한 쪽에 쏠려서 분배되는 것을 방지함.
    ex) 목적변수 Y가 25%의 0과 75%의 1로 이루어진 Binary Set일 때, stratify=Y로 설정하면 나누어진 데이터셋들도 0과 1을 각각 25%, 75%로 유지한 채 분할됨.
  • random_state: 세트를 섞을 때, 해당 int값을 보고 섞으며, 매번 데이터셋이 변경되는 것을 방지할 수 있다.

K-NN 실습

• 전체 코드

# KNN_Classifier 함수 
def KNN_Classifier(data, target, k_nb, test_size):
    """ train - test(validation) set 분리 """
    X_train,X_test,y_train,y_test = train_test_split(data,target,stratify=target, test_size=test_size, random_state=66)
    # X_train: 426  X_test: 143
	# y_train: 426  y_test: 143
    
    """ k후보군 1 ~ k_nb 개로 모델 생성 및 학습"""
    neighbors=range(1,k_nb+1)
    train_accuracy, test_accuracy = [], []
    for n in neighbors:
        # k=n으로 모델 생성
        clf = KNeighborsClassifier(n_neighbors=n)
        # 모델에 학습시키기
        clf.fit(X_train,y_train)
        # 모델의 정확도 확인
        train_accuracy.append(clf.score(X_train,y_train))
        test_accuracy.append(clf.score(X_test,y_test))
	""" 그래프로 정확도 확인 """
    plt.plot(neighbors, train_accuracy, label="train accuracy")
    plt.plot(neighbors, test_accuracy, label="test accuracy")
    plt.ylabel("accuracy")
    plt.xlabel("K (n_neighbors)")
    plt.title("KNN - Breast Cancer Classifier Accuracy")
    plt.legend()
    plt.savefig('KNN_python.png', #파일이름 
                facecolor='#eeeeee', #여백색
                edgecolor='black', #테두리색
                format='png', #파일형식
                dpi=100) #해상도(default:100)
    plt.show()

""" 유방암 데이터구조 살펴보기 """
cancer = load_breast_cancer()
# print(cancer.data) # X
# print(cancer.feature_names)
# print(cancer.target) # label(Y)
# print(cancer.DESCR)

""" KNN_Classifier 함수 실행 """
KNN_Classifier(cancer.data, cancer.target, 10, 0.25)

• 결과
  
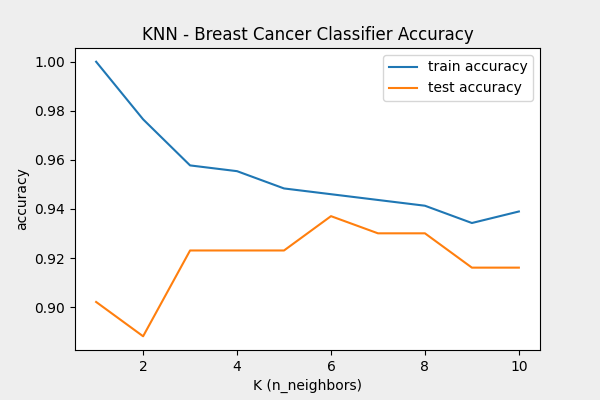
  • 그림에서 k=6일 때 테스트 정확도가 가장 높다. k<6인 경우, train accuracy는 높지만 test accuracy는 낮기 때문에 훈련 데이터에 과적합된 케이스다. 반대로, k>6일 때는 정확도가 떨어지는 과소적합의 케이스다.

Ref

• https://assaeunji.github.io/machine%20learning/2020-02-05-knn/