DFS와 BFS

🎦영상 내용 정리

깊이 우선 탐색 (DFS)

---

• 가장 직관적이고 구현하기 쉬운 탐색 방법
• 현재 정점과 연결된 정점들을 하나씩 갈 수 있는지 검사하고, 특정 정점으로 갈 수 있다면 그 정점에 가서 같은 행위를 반복한다.
• 같은 정점을 다시 방문하지 않아도 정점에 방문했다는 것을 표시해준다.
• 재귀 함수를 통해 구현한다.(동작 원리는 스택)
• 장점: 코드가 직관적이고 구현하기 쉽다.
• 단점
  • 1: 재귀 깊이가 지나치게 깊어지면 메모리 비용을 예측하기 어렵다.
  • 2: 최단 경로를 알 수 없다.

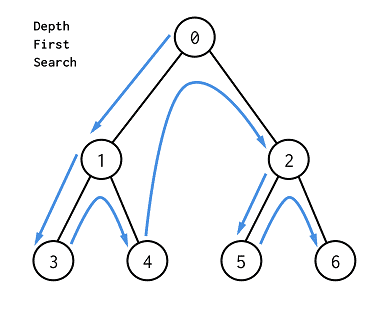
순회 흐름1. 트리

시작점에서 한 갈래로 더 이상 갈 수 없을 때까지 탐색하고, 더 갈 곳이 없다면 이전의 경로로 되돌아간다.

void DFS_Graph(int nodeId) {    // nodeId: 현재 정점을 표시하는 ID 값
	visit(nodeId);   // 방문했음 표시
	
	// 연결된 그래프들을 확인
	for (Node node : linkedNode(nodeId)) {
		if (isVisit(node.getId()) != true) {   // 아직 방문하지 않은 경우, 재귀적으로 탐색
			DFS_Graph(node.getId());
		}
	}
}

순회 흐름2. 2차원 이동

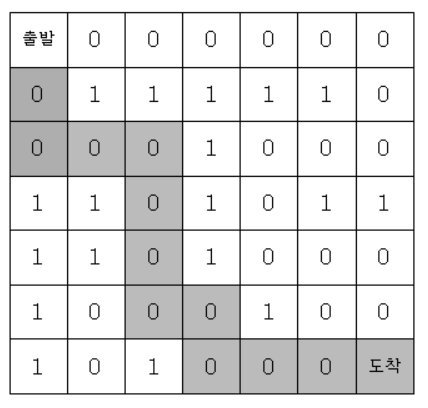
1. 현재 위치에 방문한 것을 저장
2. 내가 특정 방향으로 이동할 수 있는지 검사
   1. 이전에 방문한 적 있는지 확인
   2. 해당 위치가 좌표계 범위를 벗어나는지 확인
3. 이동할 수 있다면 이동한 위치를 재귀적으로 호출
   
   

void DFS_Coordinate(int x, int y) {   // 현재 정점의 좌표(x, y)
    visit(x, y);   // 방문했음을 표시

    // 위로 이동
    if (isValid(x, y - 1)) {
       DFS_Coordinate(x, y - 1);
    }
    // 아래로 이동
    if (isValid(x, y + 1)) {
        DFS_Coordinate(x, y + 1);
    }
    // 왼쪽으로 이동
    if (isValid(x - 1, y)) {
        DFS_Coordinate(x - 1, y);
    }
    // 오른쪽으로 이동
    if (isValid(x + 1, y)) {
        DFS_Coordinate(x + 1, y);
    }
}

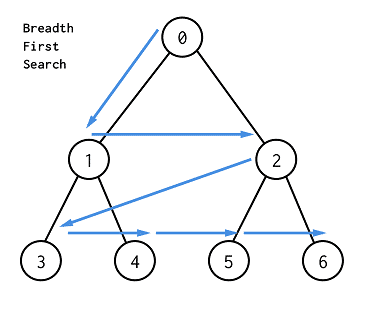
너비 우선 탐색(BFS)

---

• 시작점에서 가까운 정점부터 순서대로 방문하는 탐색 알고리즘
• 큐를 이용하여 구현
• 출발점을 먼저 큐에 넣고, 다음 로직을 반복한다.
  • 큐에 저장된 정점을 하나 Dequeue한다.
  • 그리고 Dequeue된 정점과 연결된 모든 정점을 큐에 넣는다.
  • 큐가 비어있다면 반복을 종료.
• 장점
  • 효율적인 운영이 가능하고, 시간/공간 복잡도 면에서 안정적이다.
  • 간선의 비용이 모두 같을 경우, 최단 경로를 구할 수 있다. (다를 경우 다익스트라 알고리즘 등을 활용)
• 단점
  • DFS에 비해 코드 구현이 어렵다.
  • 모든 지점을 탐색할 경우를 대비해, 큐의 메모리가 미리 준비되어 있어야 한다.

📌 DFS와 BFS의 메모리 사용량

DFS: 예상치 못한 경우에는 많은 메모리를 사용하지만, 전체적으로는 적게 든다
BFS: 메모리는 효율적으로 쓰지만 기본적으로 메모리 사용량이 많다.

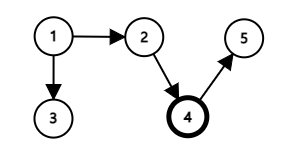
구현방법1: 그래프

1. 시작점을 큐에 넣고, 큐가 빌 때까지 루프를 돌린다.
2. 큐의 제일 앞에 있는 정점을 뽑는다.
   1. 뽑은 지점과 연결된 정점을 큐에 추가한다.
   2. 뽑은 지점이 목표 정점이라면 루프를 종료한다.
3. 만약 목표 지점을 찾지 못하더라도, 더 갈 수 있는 지점이 없으면 루프가 종료된다.
   
   

그래프	Queue

void BFS_Graph(int startNodeId) {
    queue.push(startNodeId);    // 먼저 시작점을 큐에 넣는다.

    // 큐가 빌 때까지 반복
    while(!queue.isEmpty()) {
        Long nodeId = queue.pop();   // 큐의 제일 앞에 있는 정점을 뽑는다.
        visit(nodeId);   // 뽑은 지점와 연결된 정점을 큐에 추가한다.

        if (targetId.equals(node.getId())) {   // 뽑은 지점이 목표 정점이라면 반복 종료
            return;
        }

        // 연결된 다른 정점들을 순회한다.
        for (Node node : linkedNode(nodeId)) {
            if (isVisit(node.getId()) != true) {
                queue.push(node.getId());
            }
        }
    }
}

구현방법2. 2차원 이동

Queue에 들어가는 값이 Id가 아닌 (x, y)로 바뀌는 것 빼고는 그래프와 동일하다.

void BFS_Coordinate(int start_x, int start_y) {   // 시작 지점(x, y)
    queue.push(new Position(start_x, start_y));    // 위치를 하나 뽑는다.

    // 큐가 빌 때까지 반복
    while(!queue.isEmpty()) {
        Position position = queue.pop();

        visit(position.x, position.y);   // 방문 처리

        if (targetPosition.Equals(position)) {   // 만약 목적지라면 로직 종료
            return;
        }

        // 위로 이동
        if (isValid(position.x, position.y - 1)) {
            queue.push(position.x, position.y - 1);
        }
        // 아래로 이동
        if (isValid(position.x, position.y + 1)) {
            queue.push(position.x - 1, position.y + 1);
        }
        // 왼쪽으로 이동
        if (isValid(position.x - 1, position.y)) {
            queue.push(position.x - 1, position.y);
        }
        // 오른쪽으로 이동
        if (isValid(position.x + 1, position.y)) {
            queue.push(position.x + 1, position.y);
        }
    }
}