알고리즘 - 이진 탐색

itonse·2024년 4월 18일

알고리즘

자료구조 & 알고리즘

목록 보기

2/19

1. 개념

이진 탐색 알고리즘은 정렬된 배열에서 특정 값을 빠르게 찾기 위해 사용됩니다.
탐색 과정에서 배열의 중간값과 찾고자 하는 값을 비교하여 매 단계에서 탐색 범위를 절반으로 줄이는 방식으로 동작합니다.

이 알고리즘은 평균 O(logN)의 시간 복잡도를 갖습니다.

2. 동작 방식

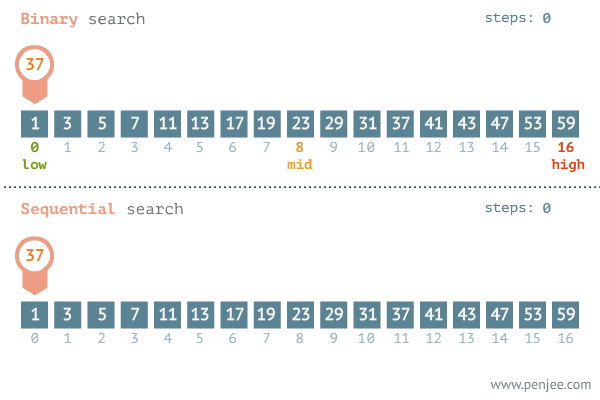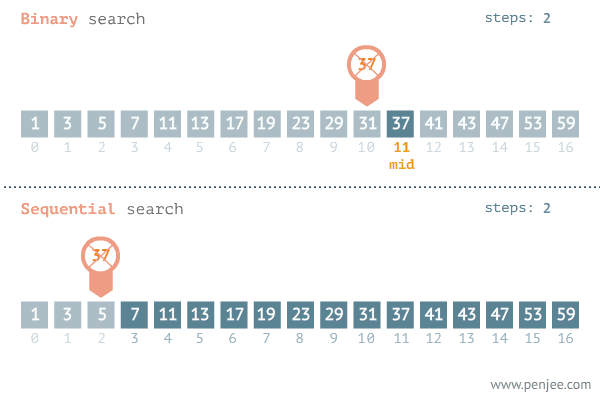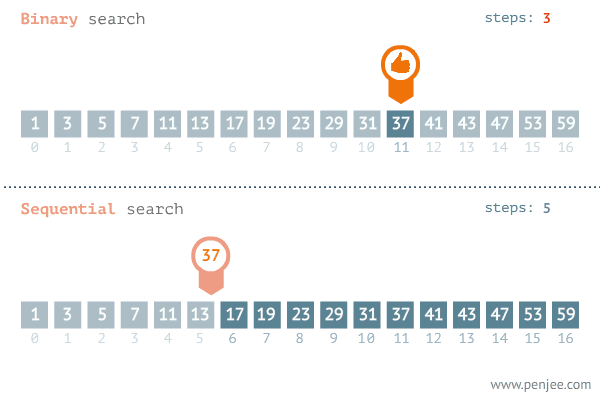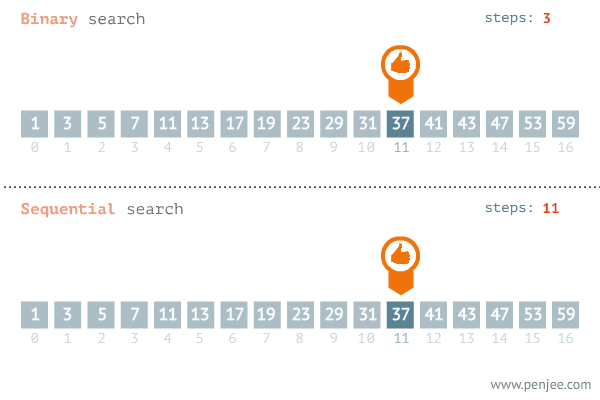
key값 37을 찾는 과정 (1~2 반복)

1. 배열의 중간 값을 가져옵니다.

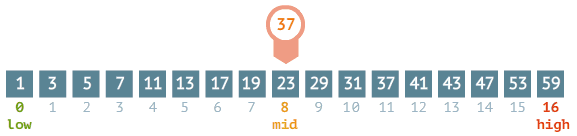
중간 값과 검색 값을 비교합니다
- 중간 값보다 검색 값이 크다면 중간값 기준 배열의 오른쪽 구간을 대상으로 탐색합니다. (low = mid + 1)
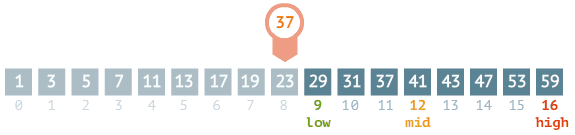
- 중간 값보다 검색 값이 작다면 중간값 기준 배열의 왼쪽 구간을 대상으로 탐색합니다. (high = mid - 1)
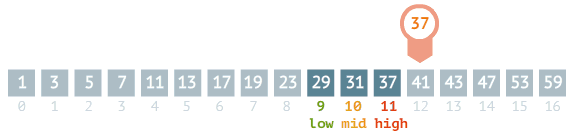
- 중간 값이 검색 값과 같다면 종료합니다.

(순차 탐색과 비교: key값 37을 찾는 과정)

3. 구현 코드

출력문에서 실행 결과를 보면 37을 찾을 시 arr에서 37이 위치한 index 11을 반환 합니다.

1. 반복문을 이용한 방법

package algorithm;
 
public class Binarysearch {
    public static void main(String[] args) {
        int[] arr = {1, 3, 5, 7, ..., 47, 53, 59};
        binarySearch(arr, 37);
    }
 
    public static int binarySearch(int arr[],  int findKey) {
        int low = 0;
        int high = arr.length - 1;
 
        // low가 high보다 작거나 같을 때 까지 반복.
        while (low <= high) {
            int mid = low + (high - low) / 2;   // 중간 인덱스 계산
 			
            // 찾고자 하는 키 값을 발견하면 해당 인덱스를 반환.
            if (arr[mid] == findKey) {
                return mid;
            }
            // 중간값보다 찾고자 하는 키 값이 크면, 검색 범위를 중간값 기준으로 오른쪽으로 조정.
            if (arr[mid] < findKey) {
                low = mid + 1;
            }
        	// 중간값보다 찾고자 하는 키 값이 작으면, 검색 범위를 중간값 기준으로 왼쪽으로 조정.
            if (arr[mid] > findKey) {
                high = mid - 1;
            }
        }
        
        // 찾고자 하는 키 값이 배열에 없으면 -1을 반환.
        return -1;
    }
}

2. 재귀 함수를 이용한 방법

public static int binarySearch(int[] arr, int find, int left, int right) {
    // 탐색 범위를 벗어났을 때 찾지 못한 것으로 -1 반환
    if (left > right) {
        return -1;
    }

    int mid = (left + right) / 2;   // 중간 인덱스 계산
    
    // 찾고자 하는 키 값을 발견하면 해당 인덱스를 반환.
    if (arr[mid] == find) {
        return mid;
    }

    // 중간값보다 찾고자 하는 키 값이 크면, 오른쪽 하위 배열에서 재귀적으로 탐색
    if (arr[mid] < find) {
        return binarySearch(arr, find, mid + 1, right);  // left을 mid + 1 값으로
    }
    // 중간값보다 찾고자 하는 키 값이 작으면, 왼쪽 하위 배열에서 재귀적으로 탐색
    return binarySearch(arr, find, left, mid - 1);  // right를 mid - 1 값으로
}