알고리즘 - Dynamic Programming(동적 계획법)

itonse·2024년 5월 7일

자료구조 & 알고리즘

목록 보기

6/19

1. Dynamic Programming 이란?

다이나믹 프로그래밍은 복잡한 문제를 여러 개의 간단한 하위 문제로 나누어 해결하는 알고리즘 설계 기법입니다. 각 하위 문제의 해답을 저장하고 재사용함으로써, 전체 문제를 효율적으로 해결할 수 있습니다.

이 방법은 특히 반복되는 계산을 많이 요구하는 문제에 효과적이며, 메모이제이션(Memoization)과 타뷸레이션(Tabulation) 두 가지 주요 방식으로 구현됩니다.

2. 다이나믹 프로그래밍의 예시

문제: 피보나치 수열의 n번째 항을 구하는 프로그램을 작성하세요.

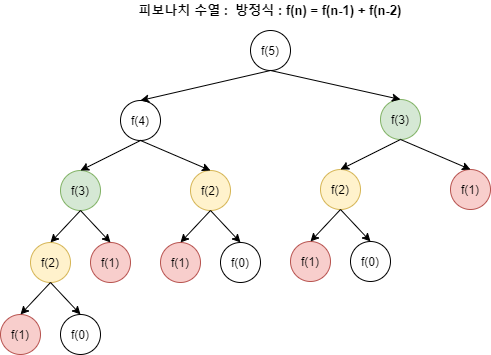
위에서 보면 f(3), f(2), f(1)과 같이 동일한 부분 문제가 중복되어 나타나는데, DP를 이용하면 1회 계산했을 때, 저장된 값을 재활용할 수 있게 된다.

(1) 메모이제이션(Memoization)을 이용한 방법

메모이제이션
탑-다운(Top-Down) 접근 방식을 따름
재귀적 구조를 사용하며, 계산 결과를 저장하는 캐시(메모리)를 사용
필요할 때만 하위 문제를 해결

public class Fibonacci {
    private static long[] memo;

    public static long fib(int n) {
        if (memo[n] != 0) return memo[n];
        if (n <= 2) return 1;
        memo[n] = fib(n - 1) + fib(n - 2);
        return memo[n];
    }

    public static void main(String[] args) {
        int n = 50; // 50번째 피보나치 수를 계산
        memo = new long[n + 1];
        System.out.println(fib(n));
    }
}

(2) 타뷸레이션(Tabulation)을 이용한 방법

타뷸레이션
바텀-업(Bottom-Up) 접근 방식을 따름
모든 하위 문제의 해답을 미리 계산하여 테이블에 저장
테이블을 순차적으로 채우며 최종 결과 도출

public class Fibonacci {
    public static long fib(int n) {
        long[] table = new long[n + 1];
        table[1] = 1;
        table[2] = 1;
        for (int i = 3; i <= n; i++) {
            table[i] = table[i - 1] + table[i - 2];
        }
        return table[n];
    }

    public static void main(String[] args) {
        int n = 50; // 50번째 피보나치 수를 계산
        System.out.println(fib(n));
    }
}