📗 Greedy
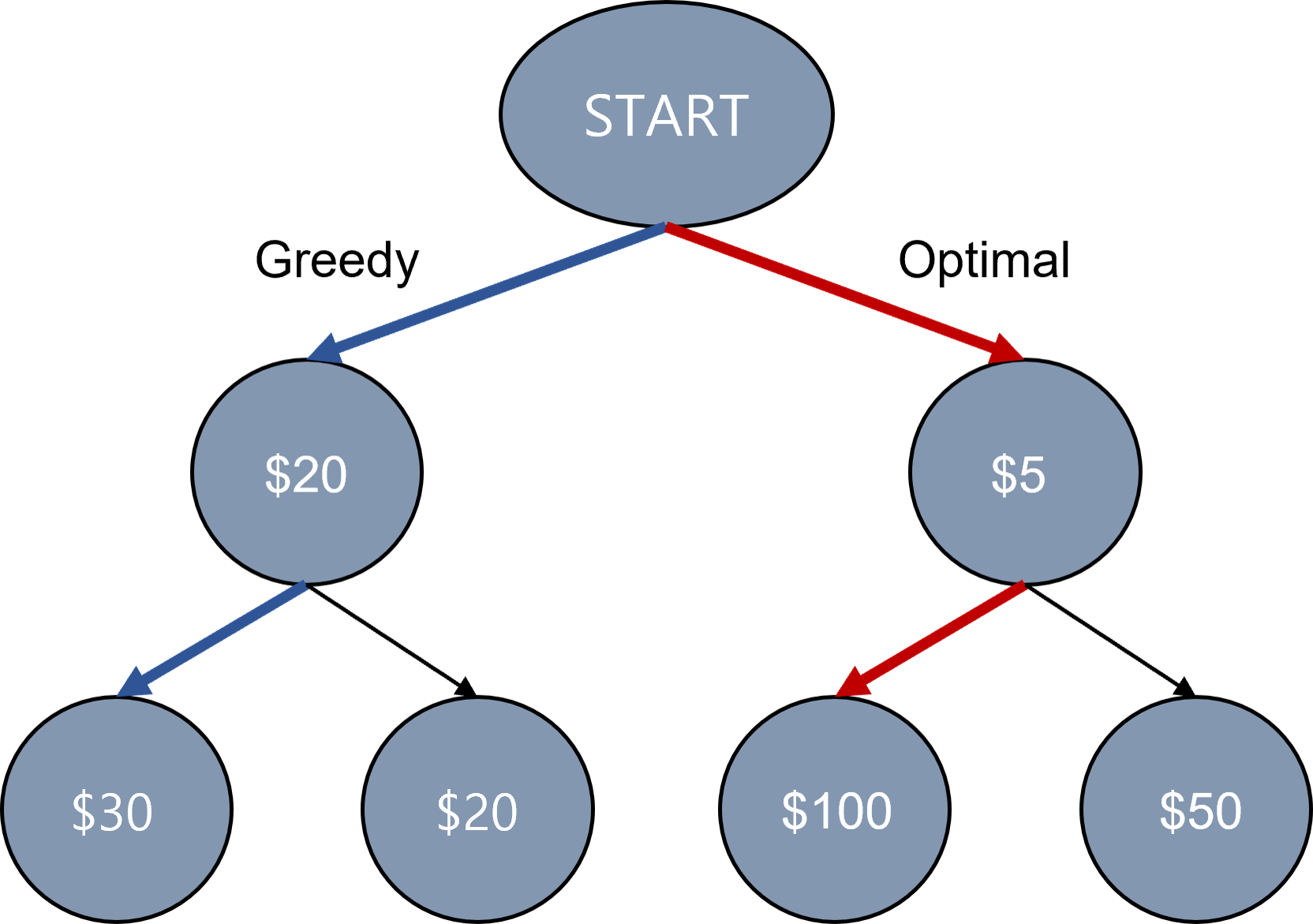
- 현재 상황에서 지금 가장 좋은 것만 고르는 방법 = 매 순간 가장 좋아 보이는 것을 선택
- 현재의 선택이 나중에 미칠 영향은 고려하지 않음
- 기준에 따라 좋은 것을 선택하는 알고리즘이므로, '가장 큰 순서대로' 또는 '가장 작은 순서대로'와 같은 기준을 제시함
- greedy 알고리즘은 최적의 해를 보장할 수 없을 때가 많음. 하지만 코딩 테스트에서 대부분의 greedy 유형은 탐욕법으로 얻은 해가 최적의 해가 되는 상황에서 이를 추론할 수 있어야 풀리도록 출제됨! - 제시되는 기준을 잘 파악할 필요가 있음
:) 주의할 점
- greedy 해법은 정당성 분석이 중요함
- 단순히 가장 좋아 보이는 것을 반복적으로 선택해도 최적의 해를 구할 수 있는지 검토
- 최단 경로를 구하는 다익스트라 알고리즘은 그리디 알고리즘으로 분류됨
🔔 Greedy 알고리즘의 정당성
- greedy 알고리즘으로 최적해를 도출하기 위해서는 2가지 조건을 만족해야함
- 탐욕적 선택 속성
- 탐욕적인 선택이 항상 안전하다는 것이 보장된다는 의미. 언제나 최적해를 보장함
- 최적 부분 구조
- 부분 최적해들이 모여 전체 최적해를 구할 수 있는 경우
🔔 Greedy 알고리즘 수행 과정
1. 해 선택
- 현재 상태에서 부분 문제의 최적 해를 구한 뒤, 이를 부분 해 집합에 추가함
2. 실행 가능성 검사
- 새로운 부분 해 집합이 실행 가능한지 확인. 문제의 제약 조건을 위반하지 않는지 검사
3. 해 검사
- 새로운 부분 해 집합이 문제의 해가 되는지 확인
- 전체 문제의 해가 완성되지 않았다면 1번 과정부터 다시 시작함
🔔 Dijkstra(다익스트라) 알고리즘
- 최단 경로 알고리즘으로 그래프에서 특정 노드에서 다른 모든 노드까지의 최단 경로를 구함
- greedy 알고리즘 기반에 동적 계획법을 활용한 알고리즘이며 그래프에서 양수 가중치만 있을 때 적용 가능
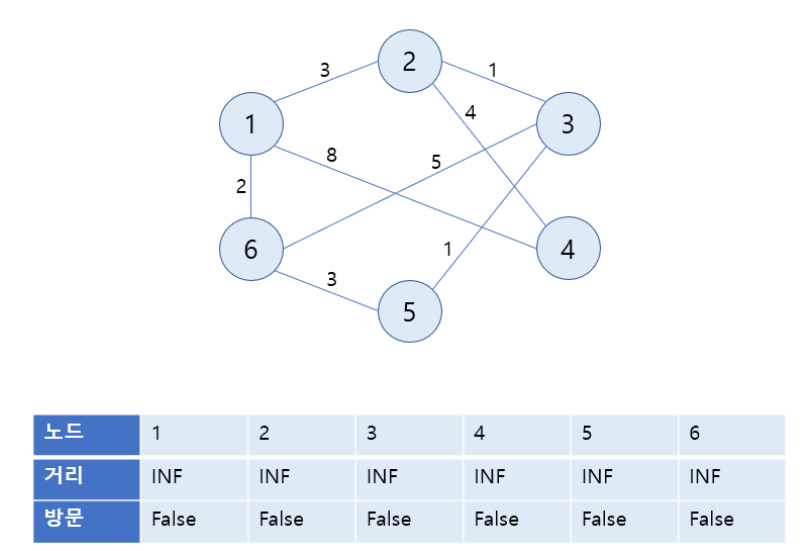
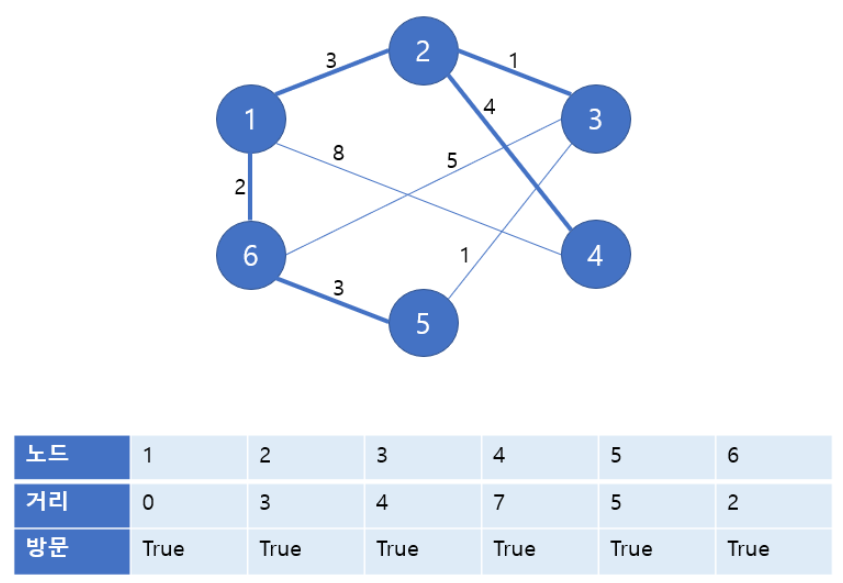
동작 설명
1. 거리, 방문 테이블 준비 (거리 테이블 : INF, 방문 테이블 : False로 모두 초기화)
2. 시작 노드 선택 (방문 처리)
3. 연결되어 있는 노드와의 최단 거리를 구함 (거리 테이블 갱신)
4. 갱신 후 아직 방문하지 않은 노드 중 가장 거리가 짧은 노드를 선택 (방문 처리)
5. 3~4번 과정 반복
순차 탐색 구현
def min_node(): # 탐색 이력이 없고 최단경로가 최솟값인 노드 반환
min_n = INF
node = 0
for i in range(1, node_cnt + 1): # 탐색이력이 없는 최단 경로를 가진 노드 탐색
if dis[i] < min_n and not visited[i]:
min_n = dis[i]
node = i
return node
def dijkstra(start):
dis[start] = 0
visited[start] = True
for i in range(1, node_cnt + 1):
if graph[start][i] != 0:
dis[i] = graph[start][i]
for i in range(node_cnt - 1):
min_node = min_node()
visited[min_node] = True
for j in range(1, node_cnt + 1):
if graph[min_node][j] != 0 and dis[min_node] + graph[min_node][j] < dis[j]:
dis[j] = dis[min_node] + graph[min_node][j]- 해당 구현 방식은 순차 탐색을 통해 최단 거리를 찾으므로 노드의 수 만큼 순차 탐색이 수행되어 O(N^2)의 시간 복잡도를 가짐
- 이를 보완하기 위해 우선 순위 큐를 사용하여 보다 효율적으로 구현할 수 있음
우선순위 큐 구현
import heapq
import sys
INF = int(1e9)
n, m = map(int, input().split())
start = int(input())
graph = [[] for _ in range(n+1)] # 그래프
distance = [INF]*(n+1) # 최단 경로 테이블
for _ in rnage(m): # 간선 초기화
node, target, cost = map(int, input().split())
graph[node].append((target, cost))
def dijkstra(start):
q = []
heapq.heappush(q, (0, start))
distance[start] = 0 # 최단경로 테이블 최적해 갱신
while q:
cost, node = heapq.heappop(q) # (비용, 현재 노드)
if distance[node] < cost : continue # 이미 방문한 노드인 경우
for next in graph[node]:
next_cost = next[1] + cost
if next_cost < distance[next[0]]:
distance[next[0]] = next_cost # 최단경로 테이블 최적해로 갱신
heapq.heappush(q, (next_cost, next[0]))
dijkstra(start)- 큐가 모두 빌 때까지 반복되므로 최대 반복횟수는 총 간선의 갯수(E)이며 한본 반복 시 O(logE )으로 힙 구조가 재배열되므로, 시간복잡도는 O(E log N)이 되고 순차 탐색보다 더 효율적으로 구현이 가능함

