Kruskal

📗 Kruskal

• greedy method를 이용해 네트워크(가중치를 간선에 할당한 그래프)의 모든 정점을 최소 비용으로 연결하는 최적 해답을 구하는 알고리즘
• 최소 신장 트리를 구하는 알고리즘 중 하나로, 그래프의 모든 노드를 연결하는 간선의 부분 집합 중에서 가중치의 합이 최소인 트리를 찾게 됨
• 시간복잡도 : O(ElogE)
  
  

🔔 신장 트리

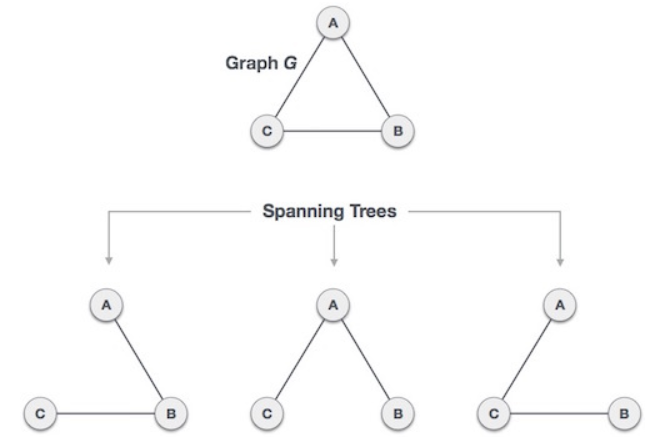
• 하나의 그래프가 있을 때, 모든 노드를 포함(연결)하되 사이클이 존재하지 않는 '부분' 그래프를 의미함
  

🔔 Kruskal 알고리즘의 동작
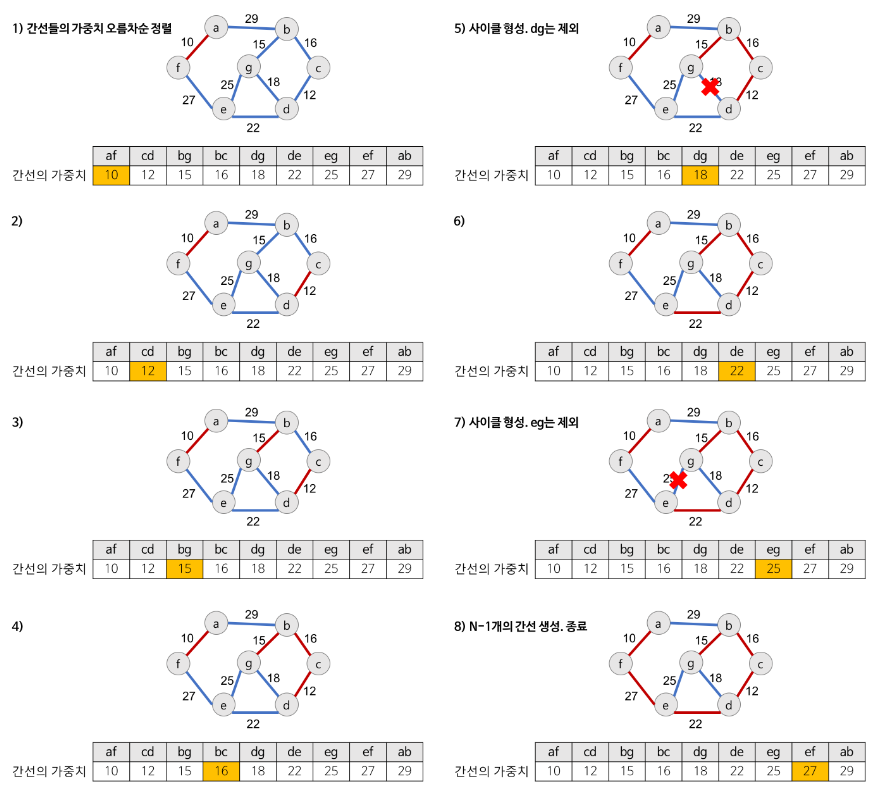
1. 그래프의 간선들을 가중치의 오름차순으로 정렬
2. 정렬된 간선 리스트에서 순서대로 사이클을 형성하지 않는 간선을 선택함
- 가장 낮은 가중치를 먼저 선택
- 사이클을 형성하는 간선을 제외
3. 해당 간선을 현재의 MST(최소 비용 신장 트리) 집합에 추가함

🔔 Kruskal 알고리즘 구현

def find_parent(parent, x):
	if parent[x] != x:
    	parent[x] = find_parent(parent, parent[x])
    return parent[x]

def union_parent(parent, a, b):
	a = find_parent(parent, a)
    b = find_parent(parent, b)
    if a < b:
    	parent[b] = a
    else:
    	parent[a] = b
        
def kruskal(graph):
	edges = []
    for node in graph:
    	for neighbor, weight in graph[node]:
        	edges.append((weight, node, neighbor))
   	edges.sort()
    
    parent = [i for i in range(len(graph))]
    mst = []
    
    for edge in edges:
    	weight, a, b = edge
        if find_parent(parent, a) != find_parent(parent, b):
        	union_parent(parent, a, b)
            mst.append(edge)
    return mst 

📘 관련 문제

⭐ 섬 연결하기