• 다음 내용은 [CS-188] Introduction to Aritificial Intelligence, UC Berkeley, Fall 2018의 Readings-Note2을 정리하였음을 밝힙니다.
• 스스로 이해하기에 영문 용어가 이해하기 직관적이면 그대로 사용했습니다.

Structure

트리 구조의 CSP 문제를 풀 때 $O(d^N)$에서 $O(nd^2)$으로 시간 복잡도를 줄일 수 있다. 이때 트리 구조라는 뜻은 제약조건 그래프 내에서 사이클이 없다는 뜻이다. 주어진 CSP가 트리 형태라면 다음과 같이 진행하자.

1. 루트 노드를 택한다. 아래 그림에서 노드 A를 루트 노드로 고르자.

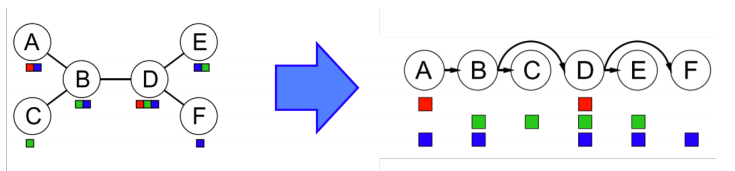
2. 트리를 사이클이 없는 방향 그래프로 만든다. 루트를 중심으로 모든 연결된 간선을 "뻗어 나가는" 형태로 만들어야 한다. 루트 노드 A가 tail이 된 형태로 연결된 간선을 연결하고, topological sort를 통해 트리를 linearlize한다.

3. arc consistenc에 따라 backwards pass한다. 즉 부모 노드의 도메인 값이 변경되면 부모 노드와 연결된 노드의 도메인 값을 확인해야 한다. 가령 노드 A와 노드 B를 비교해할 때 A의 파란색 값이 제거되고, B와 C를 비교할 때 B의 초록색 값이 제거된다.

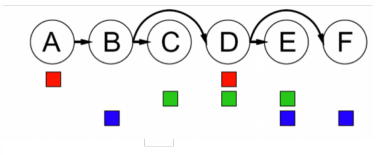
4. backwards pass(부모 노드 → 자식 노드 arc consistency 확인)이 끝난 뒤 거꾸로 forward assignment를 시작한다. 도메인 값을 확인하는 게 아니라, 정말로 각 변수에 할당할 색깔을 남아 있는 도메인에서 골라야 한다.

backwards pass에서 부모/자식 노드 간의 arc consistency를 확보했기 때문에 forward assignment 과정에서 어떤 색을 골라도 arc consistency가 사라지지 않는다. 즉 solution이 가능하다.

Cutset Conditioning

컷셋 알고리즘을 통해 위와 비슷하게 트리 형태 CSP를 풀 수 있다.

1. CSP 그래프를 CSP 트리 형태로 만들자. 즉 특정 변수들을 그래프에서 떼어냈을 때 트리가 되는 가장 작은 규모의 변수들, 컷셋(cutset)을 찾자. 아래 map-coloring 그래프에서 SA 노드를 제거하면 나머지 5개 노드는 트리가 된다. 즉 SA가 가장 작은 규모의 변수 집합, 컷셋이다.

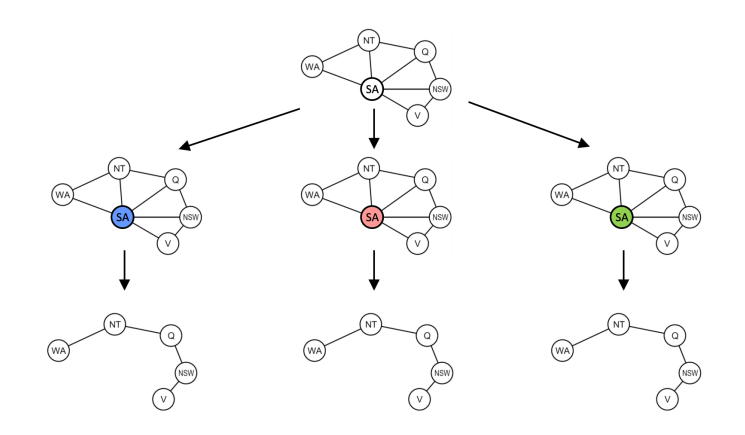
2. 컷셋을 떼어나고 남은 트리를 앞의 알고리즘(backwards pass + forward assignment)으로 풀자.

• time complexity: 컷셋의 크기를 충분히 작은 $c$라고 하자. 컷셋을 프루닝한 뒤 다시 백트래킹한다면 도메인의 크기가 $d$일 때 $d^c$번 해야 한다. 전세 변수의 개수가 $n$개이므로 트리 구조 알고리즘은 변수 $n-c$개를 각 도메인의 크기 $d$에 맞춰 두 번 확인(backward + forward)하면 된다. 즉 컷셋 크기에 따른 백트래킹 비용과 트리 구조 알고리즘 비용의 곱이므로 $O(d^c(n-c)d^2)$이다. CSP를 brute force로 풀 때에는 $O(d^N)$이 필요하다는 점에서 효율적이다.

따라서 충분히 작은 규모의 컷셋 c를 고를 수 있다면 곧바로 트리 알고리즘으로 CSP를 풀 수 있다. trade-off를 고려해 필터링과 정렬, 트리 알고리즘 중 CSP 풀이 방법을 선택하자.

Local Search

로컬 탐색 역시 백트래킹과 같이 CSP를 푸는 유용한 알고리즘이다. 최소 충돌 휴리스틱(min-conflicts heuristic)을 사용해 가장 제약 조건과 충돌이 적은 값을 변수에 반복적으로 할당해가며 답을 찾을 수 있다.

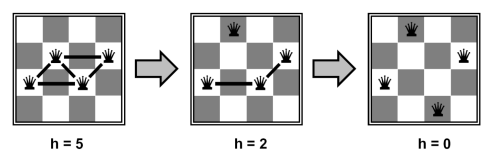
위 N-queens 문제에서 h는 퀸 사이에서 발생하는 가능한 충돌의 수로, 각 변수 퀸을 확인할 때 이를 최소화하는 값을 할당하면서 퀸의 위치를 변경한다. 반복적으로 값을 할당하면서 h==0이라는 문제 해결 상태에 도달할 때까지 로컬 탐색이 반복된다.

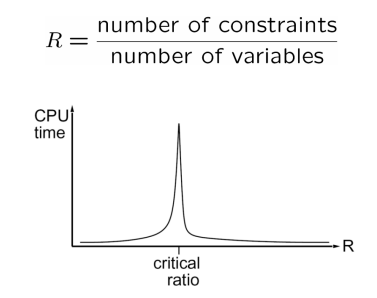
하지만 로컬 탐색은 백트래킹 알고리즘과 달리 특정 조건을 만족하지 못할 때 최적의 답을 찾지 못할 수 있다. CSP 문제의 제약 조건과 변수의 수 비율 R에 따라서 로컬 탐색에 사용되는 비용이 매우 비싸기 때문이다.

CSP 문제를 해결하는 알고리즘이 백트래킹만이 아니라 로컬 탐색 역시 있다는 사실만 기억해두자. 하지만 로컬 탐색은 특정 조건에서 매우 실용적이지 못할 수 있다.