• 다음 내용은 [CS-188] Introduction to Aritificial Intelligence, UC Berkeley, Fall 2018의 Readings-Note3을 정리하였음을 밝힙니다.
• 스스로 이해하기에 영문 용어가 이해하기 직관적이면 그대로 사용했습니다.

Summary

단순한 경로 찾기 문제가 아니라 경로를 찾는 중에 agent를 방해하는 적이 있다면 다음과 같은 알고리즘을 고려할 수 있다.

• Minimax: agent를 방해하는 적이 optimal하게 행동할 때 적용할 수 있다. 알파-베타 프루닝 기법을 통해 연산 수를 줄이는 최적화가 가능하다. expectimax 알고리즘보다 소극적으로 확장하기 때문에 미지의 적을 다룰 떄 적절하다.

• Expectimax: minimax와 달리 optimal하지 않을 수 있는 적을 상대할 때 적절하다. agent가 생각하기에 상대방의 움직임을 예상한 확률 분포를 사용해 agent가 이동할 상태에서 얻을 평균 값을 최대화한다.

agent는 어느 알고리즘을 택하느냐에 따라 위험을 감수할 수도, 위험을 피할 수도 있다. 또한 이러한 알고리즘은 agent가 적의 행동을 고려한 사전 연산을 해야 하는 까닭에 비용이 크다. 즉 어느 레벨까지 agent가 미리 계산하는지 역시 중요하다.

Games

path finding, identification 문제에서 agent는 주어진 문제의 solution을 구하기만 한다면 곧바로 행동으로 옮길 수 있었다. 하지만 게임을 하는 중 agent의 활동을 방해하는 적이 존재한다면, 사전에 계획한 경로를 그대로 따를 수 없다. 이를 적대적 탐색 문제(adversarial search problems) 또는 게임이라 한다. 게임의 특징은 다음과 같다.

1. agent가 한 행동에 따른 결정적인 / 확률적인 결과가 나온다.
2. 다양한 수의 agent(player)가 존재한다.
3. 제로 섬일 수 있다.

체커, 체스, 바둑 등 다양한 게임이 존재하며, 이는 AI가 풀었거나(solved), 푸는 중이거나, 아직 알지 못한다. 이중 고스트(적)가 등장하는 팩맨 문제는 결정론적 제로 섬 게임이다. 1). 팩맨이 행동하는 이동에 따라 결과가 결정되며 2). 팩맨의 이득이 고스트의 손실(제로 섬)이기 때문이다.

특정 게임이 AI에 의해 solved되었다는 게 무슨 뜻일까? 간략히 말하자면 게임을 하는 두 명 이상의 agent가 서로를 optimal한 플레이어로 받아들인 채 게임을 할 수 있다는 뜻이다.

이러한 적대적 탐색 문제, 게임을 풀기 위해서는 어떻게 해야 할까?

• strategy or policy: 일반적인 탐색 문제와 달리 적대적 탐색 문제는 상대방과 자신의 구성 정보를 총합해 추천받은 최고의 가능한 움직임, 전략(정책)을 따라 행동한다.

1. Game trees: One agent

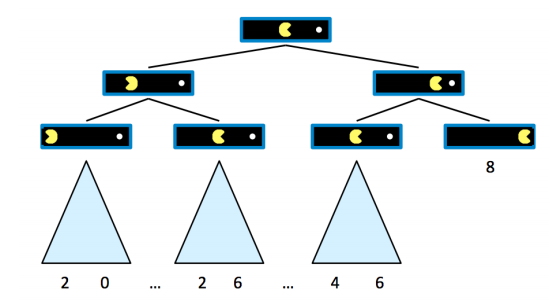
앞으로 팩맨이 어느 방향으로 어떻게 이동하는지에 따라 트리 형태로 가능한 미래를 파악할 수 있다. 여기에서 팩맨은 10점으로 시작한다. 움직일 때마다 1점씩 잃고 맨 오른쪽의 음식을 먹으면 게임이 종료된다.

수를 통해 가능한 경우의 점수를 보면 맨 오른쪽의 경우(즉 오른쪽에 있는 음식으로 직진했을 때)가 가장 높다.

• ternimal utilities: 게임이 종료되는 시점에서 팩맨이 얻을 수 있는 총 점수(utility, outcome)이다.

이 터미널 노드에서 다른 자식 노드가 이어지지 않음을 확인하자. (가장 오른쪽의 8) 수식으로 표현하면 $\forall\, terminal \,states,\,V(s)=known$

• state values: 터미널 노드가 아니기 때문에 앞으로 agent가 어떻게 움직이느냐에 따라 얻을 수 있는 terminal utilities가 달라진다.

이때 경우의 수를 통해 이 상황에서 얻을 수 있는 terminal utility의 최댓값과 최솟값을 확실히(deterministic) 고를 수 있다. 우리의 목적은 agent가 얻을 수 있는 utilities의 총합을 최대화하는 것이기 때문에, 평균도, 최소도 아니라 최댓값을 state value로 고를 수 있다. (왼쪽부터 2, 6, 6) 수식으로 표현하면 $\forall\, non-terminal \,states,\,V(s)=max_{s'\in successors(s)}V(s')$

2. Game trees: Adversary

위의 게임 트리에서 적대자가 추가되어 한 차례에는 우리가, 다음 차례에는 상대방이 움직일 수 있다. 제로 섬인 까닭에 서로의 목적은 완전히 반대다. agent는 상대를 피해 최대한 많은 점수를 얻어야 하는 반면, 상대는 우리를 잡으려 달려들 것이다.

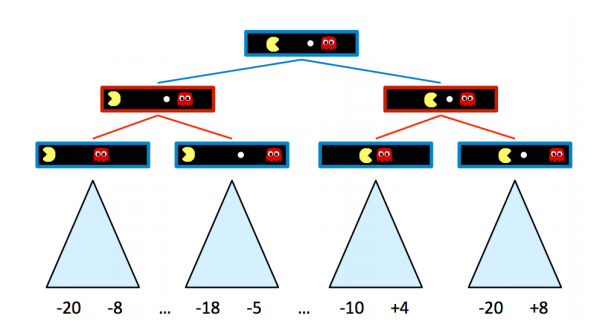
앞에서 정의한 state value가 여기에서도 (agent의 입장에서) 유용하게 사용된다. 위 그림에서 팩맨이 고를 수 있는 점수의 최대치를 기준으로 삼자면, 왼쪽에서 -8, -5, -10, +8이 state value다. 이때 팩맨은 어떤 선택지를 골라야 적을 피해 점수를 얻을 수 있을까? 미니맥스 알고리즘은 적이 optimal하게 행동한다고 가정한 뒤, 우리가 얻을 수 있는 최적의 점수를 얻어낸다.

Minimax

미니맥스 알고리즘을 통해 제로 섬 게임의 해결책을 찾을 수 있다. 미니맥스에서 적은 항상 optimal하게 행동한다. 즉 언제나 최악의 상황, worst case를 고려한다. 모든 레벨에서 점수를 최대화하지 않고 미니맥스 알고리즘은 다음 정책을 따른다.

• 자신의 차례: state value를 최대화
• 상대방의 차례: state value를 최소화

언제나 optimal한 적은 우리가 얻을 수 있는 최댓값을 얻도록 허용하지 않는다. 차라리 이를 계산해서 최대한 얻을 수 있는 선에서의 최댓값을 얻는데 관심을 기울이자.

그렇기 때문에 각 레벨에서의 state value를 표현하는 수식은 앞의 게임 트리에서 $\forall\, opponent-controlled \,states,\,V(s)=min_{s'\in successors(s)}V(s')$를 추가한 것이다.

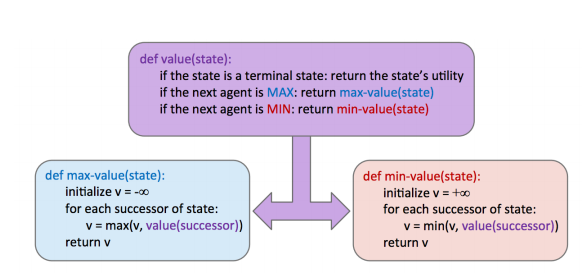
Alpha-Beta Pruning

미니맥스 알고리즘은 최악의 경우에서 상대방을 피해 얻을 수 있는 최적의 값을 반환하지만, 각 레벨의 state value를 반환하기 위해 엄청난 노드를 연산해야 한다. 트리의 깊이를 $m$, branching factor가 $b$라고 할 때 시간 복잡도는 $O(b^m)$이다. 그렇다면 미니맥스 알고리즘의 연산량을 줄일 수 있는 방법이 없을까?

알파-베타 프루닝은 미니맥스 알고리즘의 최댓값/최솟값을 확인할 때, 특정 위치의 값이 정해진다면 다른 노드 값은 확인 안 해도 결과가 같다는 데에서 출발한다.

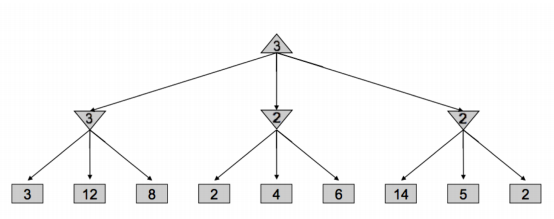
삼각형을 우리, 거꾸로 된 삼각형을 상대방의 차례라고 생각하자. 삼각형은 자식 노드의 state values 중 최댓값을, 거꾸로 된 삼각형은 그 중 최솟값을 골라야 한다. (탐색 및 확인 방향이 왼쪽부터라 가정한다)

1. 상대방: 맨 왼쪽 노드에서 3을 고른다. 이 레벨 위에서 우리가 택할 로컬 최댓값이 3으로 설정된다.
2. 상대방: 중간 노드에서 2를 확인한다. 이때 나온 2가 왼쪽 노드에서 고른 3보다 작다. 즉 다른 값을 확인해 설령 2보다 작은 1이 나오더라도 윗 단계에서 이 값이 뽑힐 일은 없다. 그렇기 때문에 탐색을 중단한다.
3. 상대방: 맨 오른쪽 노드에서 14, 5, 2 순서대로 노드를 확인한다. 2가 나올 때까지 값을 확인하는 건 이전과 달리 14와 5가 이 레벨의 로컬 최댓값 3보다 크기 때문이다.

미니맥스 알고리즘을 통해 얻은 게임 트리의 각 노드 별 state value가 알파-베타 프루닝의 state value와 정확히 일치하지 않을 수도 있는데, 도중 프루닝할 수도 있기 때문이다. 하지만 결과적으로 루트 노드에 반환되는 값은 같다.

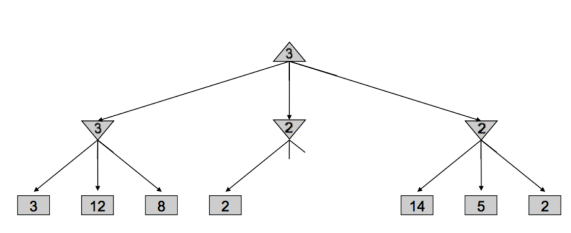
다시 말해 굳이 계산하지 않아도 결과를 알 수 있는 부분은 가지 치기를 통해 넘어가 연산 과정을 생략할 수 있다. 알파-베타 프루닝은 각 최댓값/최솟값을 고르는 단계에서 루트까지의 가장 좋은 선택지를 계속해서 비교해간다.

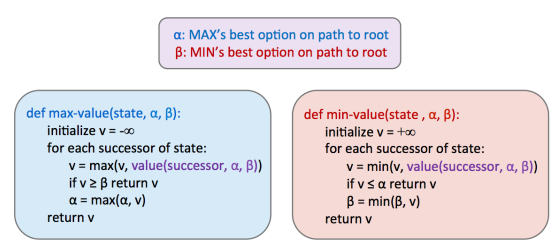
Evaluation Functions

하지만 알파-베타 프루닝으로도 미니맥스에 필요한 연산량을 감당하기 힘들다. 대신 추정 함수를 통해 실제 state value의 추정치를 얻어내자.

깊이 제한 미니맥스 알고리즘은 추정 함수를 사용해 실제로는 터미널 노드가 아닌 노드를 마치 터미널 노드처럼 다루면서 확실한(determined) 선택지를 확인한다. 따라서 (추정 함수의 성능에 따라서) optimal한 경로를 찾지 못할 수도 있다.

물론 추정 함수는 더 깊이 있는 노드까지 다룰 수록 성능이 높다. 이 함수는 입력 상태 s의 feature와 할당된 비용 w 등을 통해 계산한 함수 $Eval(s)=w_1f_1(s)+...+w_nf_n(s)$로 표현된다.

미니맥스 알고리즘은 determisitic한 게임의 경로를 반환하지만, 실제 게임 환경 상 모든 state value를 계산할 수는 없다는 점에서 추정치를 활용한다. 이를 통해 비용 대 정확도라는 trade-off가 발생한다. 이를 주의하면서 이후 expectimax 알고리즘 어떻게 non-deterministic 또는 stochastic 게임을 다루는지 살펴보자.