• 다음 내용은 [CS-188] Introduction to Aritificial Intelligence, UC Berkeley, Fall 2018의 Readings-Note3을 정리하였음을 밝힙니다.
• 스스로 이해하기에 영문 용어가 이해하기 직관적이면 그대로 사용했습니다.

Expectimax

미니맥스는 optimla한 상대방을 가정하므로 최악의 경우 얻을 수 있는 가장 좋은 solution을 준다. 하지만 상대방이 언제나 optimal하게 행동하지 않는다면? 또는, 상대방이 언제나 optimal하다고는 할 수 없는 주사위와 같은 확률 게임이라면 어떨까? 따라서 미니맥스의 state value는 주어진 상황에서 agent가 택할 수 있는 확률을 상정해야 한다.

• chance states: 확실하게(deterministic) 자식 노드를 고를 수 없기 때문에 각 successor를 택하는 확률을 이용해 총 기댓값을 계산한다. $\forall chance\,states,\,\,\,\,V(s)=\sum_{s' \in successors(s)} p(s'|s)V(s')$

$p(s'|s)$를 통해 주어진 상태 s에서 s'로 이동할 수 있는 확률을 얻고, 그 상태 s'에서 나오는 state value 합을 현재 chance state의 값으로 삼자.

Expectimax는 현재 주어진 chance nodes에 연결된 '모든' successor를 판단해야 한다. 반면 Minimax는 이 successor 중 값이 가장 낮은 노드만을 택한 알고리즘이다.

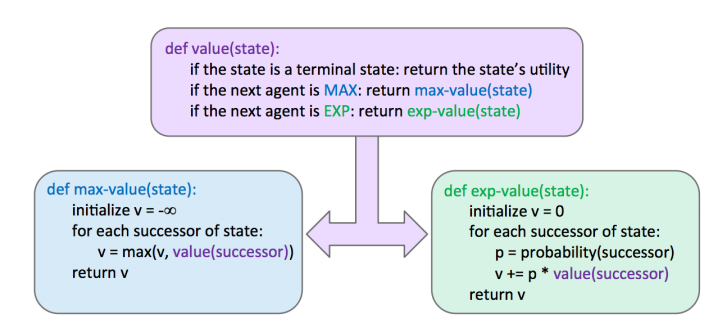
미니맥스와 달리 평균값(exp-value로 구함)이 가장 높은 길을 택하는데, 그 과정에서 이 길로 이어지는 확률이 포함되어 있다.

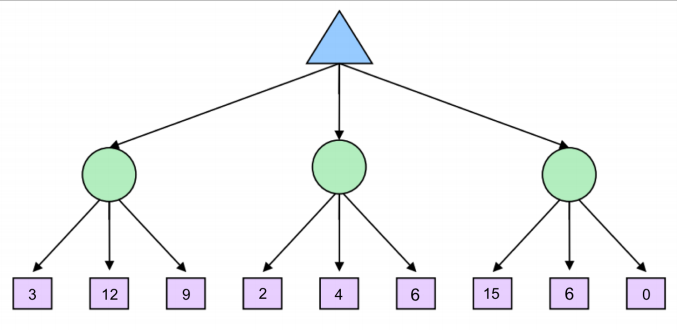
expectimax 알고리즘은 위 게임 트리의 삼각형이 세 개의 chance states 중 하나를 택할 때 평균 기댓값을 바탕으로 선택한다. 위 경우 모든 경우가 $\frac13$이므로 왼쪽에서부터 8, 4, 7이 나오기 때문에 가장 높은 값인 왼쪽 길을 택할 것이다.

평균 값을 계산하기 위해서는 chance states의 모든 successor를 살펴보아야 하기 때문에 알파-베타 프루닝은 적용할 수 없다.

Layers and general Games

앞에서 살펴본 minimax와 expectimax는 일 대 일 상황(팩맨 대 고스트)을 가정한 단순한 경우이기 때문에 게임이 어떻게 구현되었는지 파악한 뒤 레이어를 추가할 수 있다. 이 경우 최댓값과 최솟값을 구하는 레이어에 몇 개의 노드를 둘 것인지, 모든 상대방이 optimal한지 등을 확인하자.

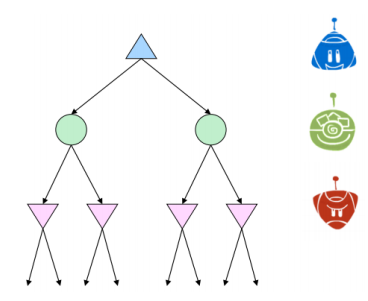
위 게임에서는 팩맨 차례가 끝난 뒤 네 마리 고스트 차례로 넘어간다. 이때 팩맨은 이들이 optimal하지 않다고 가정, 확률적으로 가장 높은 점수를 얻을 expectimax 알고리즘을 따르고 있다.

multi-agent가 하는 게임인 경우 역시 게임 트리를 새롭게 구성할 수 있다.

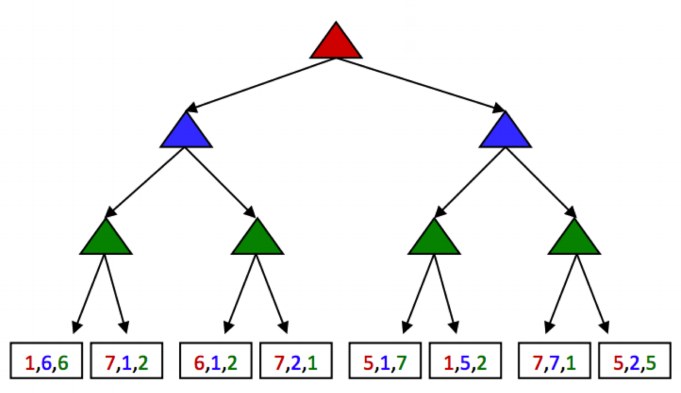
자기 차례에서 자신만의 가장 '큰' 점수를 고려하는 세 명의 agent는 어떤 선택을 할까? 초록색은 각각 (1,6,6), (6,1,2), (5,1,7), (5,2,5)를 고른다. 이후 파란색은 (1,6,6), (5,2,5)를, 마지막으로 빨간색은 (5,2,5)를 고른다.

이 과정에서 agent는 자신의 점수만을 신경쓰는 것보다 이후에 고를 다른 agent와 협력하는 게 더 이득일 수도 있다.

Utilities

합리적인 게임 agent의 행동 원칙은 언제나 (게임을 시작할 때 정해진) utility를 극대화하는 것이다. 하지만 특정한 규칙만 따른다고 모든 선택이 이 원칙과 부합하는 것은 아니기 때문에, 다음 5가지 원칙을 지켜야 한다.

1. Orderability: A와 B의 중 하나를 일관되게 고를 수 있다.
2. Transitivity: A보다 B를 선호하고 B보다 C를 선호할 때, A보다 C를 선호해야 한다.
3. Continuity: A를 B보다, B를 C보다 선호할 때 A와 C를 통해 B를 구할 수 있다.
4. Substitutability: A와 B 선호도가 같다면 A를 B로, B를 A로 바꾼 선택지도 상관없다.
5. Monotonicity: A를 B보다 선호하고 이 두 가지 길만 있는 선택지가 주어지면 A에 더 큰 확률을 할당하는 선택지를 선호한다.

이 다섯 가지를 지킬 때 agent는 곧 utility를 극대화하는 합리적(rational)인 존재라고 할 수 있다. 이 agent가 주어진 정책에 따라 위험을 부담할 수도, 위험을 감수하지 않을 수도 있다.