[CS-188] Note4: MDPs

Junyoung Park·2022년 2월 17일

CS-188

목록 보기

12/23

다음 내용은 [CS-188] Introduction to Aritificial Intelligence, UC Berkeley, Fall 2018의 Readings-Note4을 정리하였음을 밝힙니다.
스스로 이해하기에 영문 용어가 이해하기 직관적이면 그대로 사용했습니다.

Non-Deterministic Search

비결정적 탐색 문제는 현재 노드의 같은 action으로 이어질 수 있는 successor가 동시에 여러 노드인 문제이다. 이전 결정적 탐색 문제에서는 action만 고른다면 그 이후에 어떤 successor 노드가 올지는 아무런 의심 없이 확신할 수 있었다. 하지만 비결정적 탐색 문제에서 다음 successor가 어떤 값이 될지는 확신할 수 없는 불확실성 uncertainty의 영역이다. 이 문제를 어떻게 해결할 수 있을까? MDP라 불리는 마르코프 의사 결정 과정을 통해 풀 수 있다.

MDPs

마르코프 결정 과정은 다음과 같은 요소로 정의된다.

상태 S
행위 A
시작 상태
한 개 이상의 종료 상태
discount factor $\gamma$
트랜지션 함수 $T(s,a,s')$ : 비결정적 탐색 문제에서 주어진 상태 s에서 특정 행위 a를 할 때 어떤 상태 s'가 나올지는 확률적으로 표현할 수 있다.
보상 함수 $R(s,a,s')$ : MDP 문제는 종료 상태에서 받는 "큰" 보상과 각 단계에서 agent가 살아 있다면 받는 "작은" 보상이 있다. 합리적 agent는 자신이 받는 보상을 최대화하는 행동을 택해야 한다.

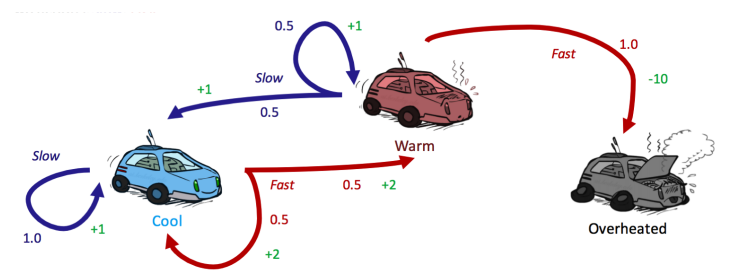
위의 상태 공간 그래프은 각 상태 s에서 확률적으로 어떤 다음 상태 s'가 오는지, 그리고 그에 따른 보상 R을 보여준다. 이때 overheated될 때 보상이 -10으로 음수일 수도 있다.

처음 시작 상태를 $s_0$ 이라고 한다면 이 때 택하는 행위 $a_0$ 에 따라 $s_1$ 이 확률적으로 결정된다. $s_0 \rightarrow a_0\rightarrow s_1 \rightarrow a_1 ...$ 이 상황에서 agent가 보상을 최대화하려면 $U([s_0,a_0,s_1,a_1,...])=R(s_0,a_0,s_1)+R(s_1,a_1,s_2)+...$ 를 통해 utility 함수를 표현할 수 있다.

위 상태 공간 그래프처럼 MDP는 탐색 트리로 표현할 수 있다. 시작 상태 $s_0$ 이 cool한 자동차일 때 선택 a를 두 번할 수 있다면 나올 수 있는 가능한 모든 상황을 트리로 구조화했다.

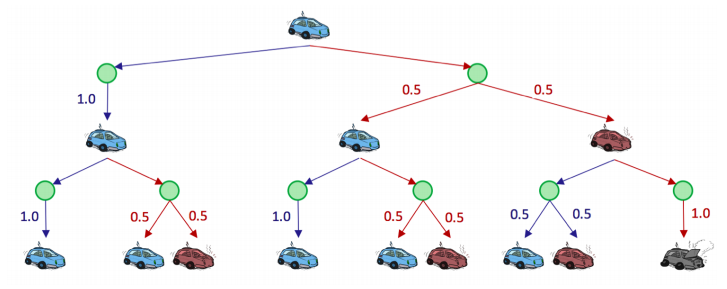
초록색 원 노드는 지금 상태 s에서 선택 a를 했지만 이후 s'가 결정되지 않은 상황 그 자체를 표현하고 있다. 이를 q-state 또는 action state라고 한다.

1. Finite Horizons and Discounting

위 트리는 agent가 얻을 수 있는 가장 큰 보상은 무엇일까? 정답은 무한이다. 언제나 파란색 a, 즉 slow라는 선택지를 고른다면 overheated되는 위험 없이 보상을 늘려 나갈 수 있다. 하지만 이런 가정은 agent가 택할 수 있는 행위에 1). 개수 제한을 두지 않았을 때, 또는 2). 각 상태에서 받는 보상 값을 모두 같다고 평가할 때 비로소 성립한다.

finite horizons: 트리 깊이를 n으로 제한해 agent가 택할 수 있는 action 개수를 제한한다. 어떤 종류의 상태더라도 타임 스탬프 n에 agent가 있는 상태 s가 종료(터미널) 상태가 된다.
discounting: 지금 agent가 있는 타임 스탬프 t의 상태를 $s_t$ 이라고 하자. 이때 t단계에서 고려할 보상에 이후에 t+1, t+2.. 단계에서 얻을 보상보다 가중치를 둔다는 개념이다.

즉 미래보다 현재 얻는 보상에 집중하는 discounting은 이 가중치 $\gamma$ 를 이후 미래 상태 t+1, t+2에 반복해서 곱해나가면서 그 가중치를 줄인다. 따라서 MDP의 agent가 utility를 최대화하기 위해 세운 utility 함수 $U([s_0,a_0,s_1,a_1,...])=R(s_0,a_0,s_1)+R(s_1,a_1,s_2)+R(s_2,a_2,s_3)...$ 에 $\gamma$ 를 사용해, $U([s_0,a_0,s_1,a_1,...])=R(s_0,a_0,s_1)+\gamma R(s_1,a_1,s_2)+\gamma^2R(s_2,a_2,s_3)...$ 를 구할 수 있다.

이때 discounting factor $\gamma$ 의 범위는 $0<\gamma<1$ 이다. 따라서 지금 상태보다 무한한 거리만큼 떨어진 상태의 보상은 따라서 0에 가깝다. 이를 반영해서 다시 utility 함수를 표현하면, $U([s_0,a_0,s_1,a_1,...])=\sum^{\infty}_{t=0} \gamma^t R(s_t,a_t,s_{t+1}) \geq \sum^{\infty}_{t=0}\gamma' R_{max}=\frac{R_{max}}{1-\gamma}$

2. Markovianess

MDP의 markovian이라는 용어는 미래와 과거 상태가 조건적으로 독립되어 있다는 Markov property 또는 memoryless property를 만족할 때 사용할 수 있다. 즉 현재 상태가 주어지기만 하면 과거 상태를 알 필요 없다는 말이다. 과거 상태를 아는 것은 미래 상태를 파악하는 데 그 어떤 영향도 미치지 않는다.

여태까지 방문한 상태 $s_0,s_1,...,s_t$ 에서 agent가 한 $a_0,a_1,...,a_{t-1}$ 이 주어진다면, $P(S_{t+1}=s_{t+1}|S_t=s_t,A_t=a_t,S_{t-1}=s_{t-1},A_{t-1}=a_{t-1},...,S_0=s_0)$ 으로 표현할 수 있다.

하지만 이때 $S_{t+1}$ 를 결정하는 요소에는 현재 상태 $s_t$ 와 $a_t$ 만 있으면 된다. 앞의 확률은 $P(S_{t+1}=s_{t+1}|S_t=s_t,A_t=a_t)$ 로 짧게 표현된다.

Markovianess 또는 memoryless라는 용어를 통해 MDP의 다음 상태를 확인하기 위해 필요한 건 현재 상태일 뿐임을 기억하자. 따라서 트랜지션 함수 T는 곧바로 현재 상태에서 다음 상태를 꺼내오는 확률이다. $T(s,a,s')=P(s'|s,a)$

3. Solving MDPs

optimal policy $\pi^* : S \rightarrow A$ 를 통해 보상 기댓값을 최대화한다.

a	b	c	d	e
10				1

이 MDP 문제를 풀어보자. $S={a,b,c,d,e}, A={East,West,Exit}$ 인 MDP 문제에서 Exit는 상태 a 또는 e에서만 사용 가능하며, discounting facotr $\gamma=0.1$ 이다. 이때 어떤 정책을 사용할 수 있을까? e보다 a에서 Exit할 때 얻을 수 있는 보상이 더 크다. 각 상태 s에서 a에 대한 기댓값을 확인해보자.