• 다음 내용은 [CS-188] Introduction to Aritificial Intelligence, UC Berkeley, Fall 2018의 Readings-Note7을 정리하였음을 밝힙니다.
• 스스로 이해하기에 영문 용어가 이해하기 직관적이면 그대로 사용했습니다.

Decision Networks

의사결정 네트워크를 통해 확률 분포를 나타내는 그래프가 주어질 때 유틸리티를 기반으로 특정 액션이 어떻게 영향을 미치는지 모델링할 수 있다. 의사결정 네트워크는 다음과 같은 노드로 구성된다.

• 기회 노드(Chance nodes): 베이즈 넷의 기회 노드와 똑같은 개념이다. 연결된 노드와 관련된 확률을 가지고 있다.

• 액션 노드(Action nodes): 노드의 행동을 완전히 통제할 수 있는 노드다. 주어진 상태에서 할 수 있는 모든 행위들 가운데 하나를 택할 수 있다.

• 유틸리티 노드(Utility nodes): 기회 노드와 액션 노드를 부모로 둔 자식 노드로, 부모 노드가 가진 값에 따라 다른 결과값을 출력하는 노드다.

1. Weather and Umbrella

30% 확률로 비가 온다고 할 때, 우산을 들고 가야 할까? 비가 올 확률이 80%로 높아진다면 어떻게 해야 할까? 이러한 문제를 의사결정 네트워크로 표시해보자.

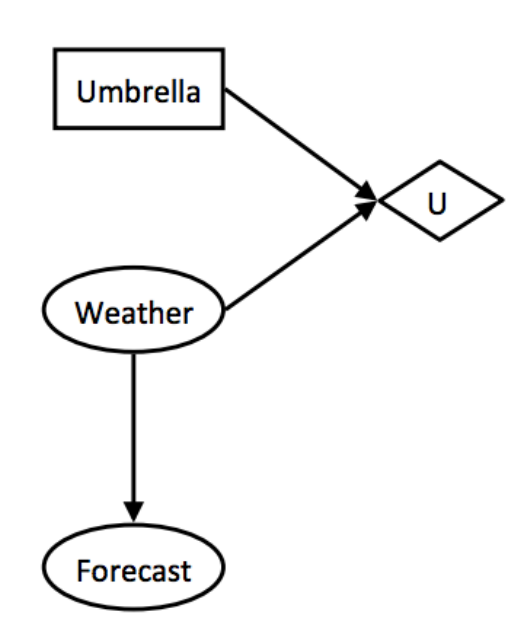
우산을 들고 가느냐에 따라 유틸리티가 결정된다고 가정해보자. 비가 올 때 우산을 들고 간다면 유틸리티가 높겠지만, 오지 않을 때 들고 간다면 낮을 것이다. 비가 오지 않는 경우 역시 마찬가지다. 날씨를 추측할 수 있는 예측 확률을 통해 우산을 들고 가는 액션을 결정하고, 이를 통한 유틸리티의 기댓값을 따져볼 수 있을 것이다.

이처럼 상황 별로 유틸리티가 주어질 때, 우리는 유틸리티 기댓값을 확률적으로 구할 수 있다. 즉 MEU(maximum expected utility)를 구한다면 가장 큰 유틸리티를 가장 높은 확률로 얻을 수 있다.

1. 알고 있는 에비던스부터 시작해, 유틸리티 노드를 자식으로 둔 기회 노드의 사후 확률을 계산한다.
2. 사후 확률을 통해 각 액션 노드에서 이어지는 유틸리티 기댓값을 구할 수 있다. 에비던스 e와 기회 노드 n개가 주어질 때 액션 a를 하고 얻는 유틸리티 기댓값은 이렇게 구한다.

$EU(a|e)=\sum\limits_{x_1,...,x_n}=P(x_1,...,x_n|e)U(a,x_1,...,x_n)$

유틸리티 값에 $P(x_1,...,x_n|e)$라는 가중치를 곱하는 게 곧 기댓값이라는 데에 주의하자.

3. 유틸리티 기댓값 중 최댓값(MEU)으로 이어지는 액션을 고른다.

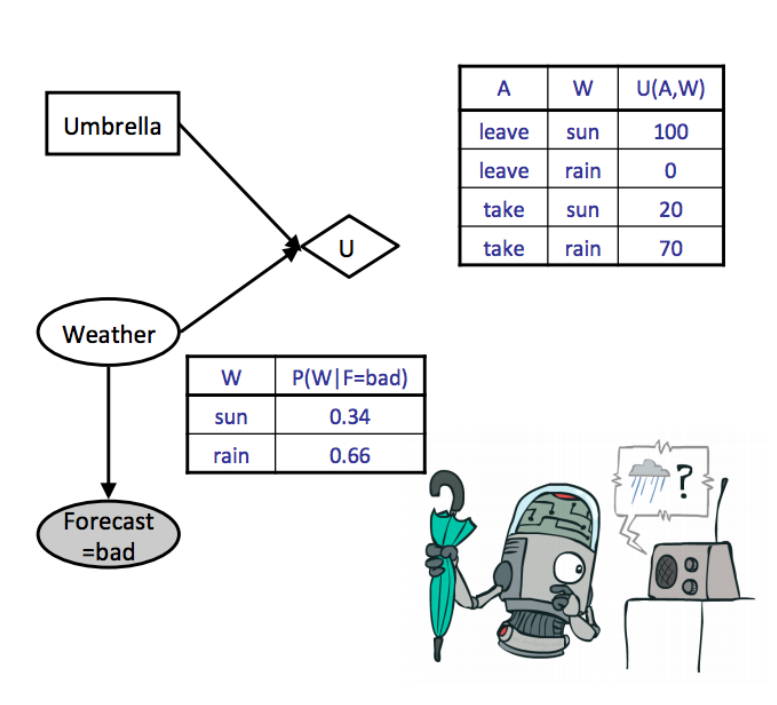
위 확률 분포를 사용해 날씨가 나쁠 때 우산을 들고 가거나 놔두고 나갔을 때 얻을 유틸리티 기댓값을 구해보자.

1. $EU(leave|bad)=\sum\limits_{w}P(w|bad)U(leave,w)=0.34*100+0.66*0=34$
2. $EU(take|bad)=\sum\limits_{w}P(w|bad)U(take,w)=0.66*20+0.34*70=53$

따라서 MEU는 53인 $EU(take|bad)$로 유틸리티가 이 조건일 때 우산을 들고 나가는 선택이 더 합리적임을 구할 수 있다.

2. Outcome Trees

의사결정 네트워크를 특정 노드에서 이어지는 트리 구조로 표현할 수도 있다. 위 문제를 날씨가 좋거나 나쁠 확률, 우산을 들고 가거나 놔두고 갈 상황에 따라 갈라지는 트리로 표현할 수 있다.

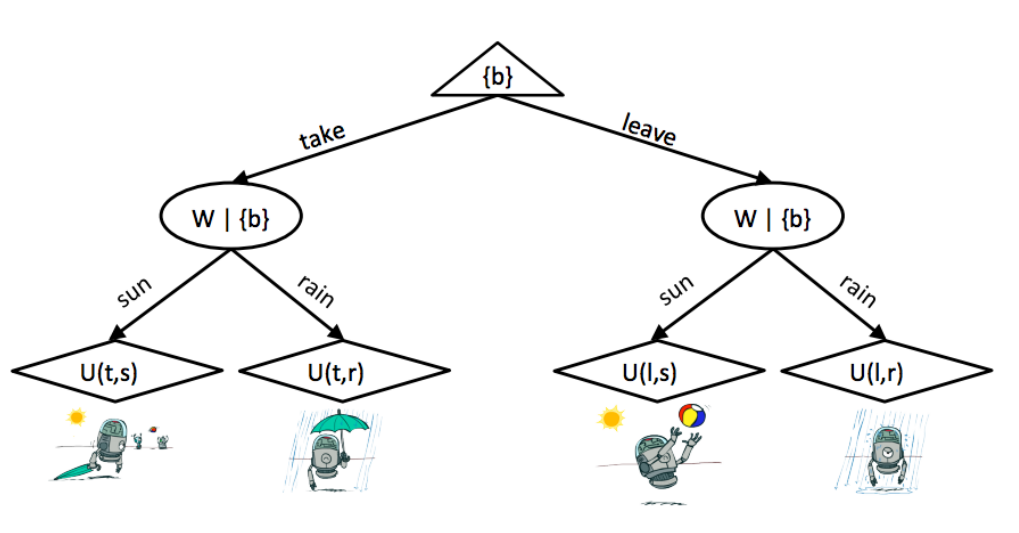
expectimax와 마찬가지로 루트 노드는 자식 노드 중 유틸리티가 더 높은 값을 택하는 maximizer 노드로 MEU를 구하기 위함이다.

The Value of Perfect Information

정확한 MEU를 구하기 위해서는 현재 노드 입장에서 많은 에비던스를 모아 유틸리티 기댓값을 계산해야 한다. 트리 구조를 통해 비유하자면, 루트 노드에서 탐색해야 하는 깊이, 연산량이 매우 많아질 것이다. 문제를 해결하기 전에 모든 에비던스가 주어지면 좋겠지만, 실제 문제를 풀 때에는 에비던스 관측값을 구하는 비용 역시 생각해야 한다.

완벽한 정보를 얻어내는 데 비용을 더 쓸 것인가, 혹은 이 정도로 만족한 채 유틸리티 기댓값을 구하는 액션을 지금 바로 정할 것인지 에이전트는 결정해야 한다.

VPI(Value of Perfect Information)를 통해 에비던스를 얼마나 관측하는 게 가장 효율적인 선택인지 비교할 수 있다.

1. General Formula

에비던스 e가 주어질 때 MEU는 이렇게 적을 수 있다.

$MEU(e)= max_{a} \sum\limits_{s}P(s|e)U(s,a)$

이때 에비던스 e'를 액션 a를 고르기 전에 관측했다고 가정해보자. MEU 역시 바뀐다.

$MEU(e, e')= max_{a} \sum\limits_{s}P(s|e, e')U(s,a)$

그런데 이때 e'를 얻었어도 정확히 어떤 상황이 될지 모른다. 액션을 취하기 전에 에비던스를 얻었기 때문이다. 따라서 이 상황을 랜덤 변수 E'로 표현해 MEU에 대한 MEU를 구해야 한다.

$MEU(e,E')=\sum\limits_{e'}P(e'|e)MEU(e,e')$

정리하자면 새로운 에비던스를 관측해 MEU를 구하려면 현재 가진 MEU 값을 다시 활용해야 한다.

VPI는 이렇게 에비던스 e'를 관측하기 전후의 MEU 두 개를 통해 구할 수 있다. 요점은 이 에비던스를 관측해서 얻을 수 있는 유틸리티 기댓값이 얼마나 더 많아지는지다.

$VPI(E',e)=MEU(e,E')-MEU(e)$

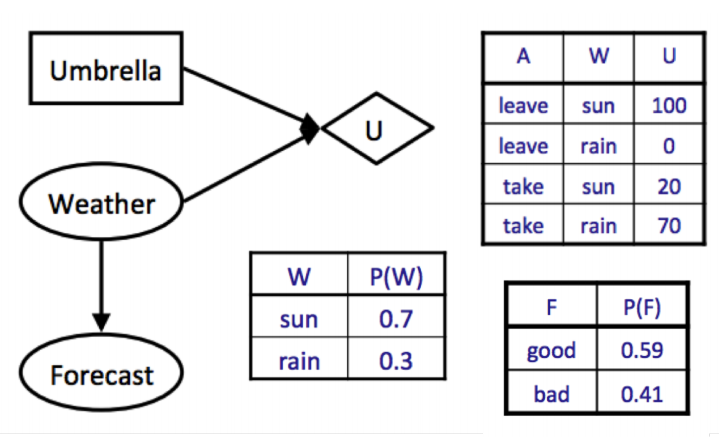
일기예보 P(F)가 없을 때 MEU를 구해보자.

$MEU(\empty)=max_aEU(a)=max_a\sum\limits_wP(w)U(a,w)=max{70,35}=70$

에비던스가 없다면 MEU인 70으로 이어지는 우산을 놔두고 가는 행동을 골라야 한다.

이때 기상예보 확률에 관한 에비던스가 관측되었다.

$MEU(e,E')=MEU(F)=\sum\limits_{e'}P(e'|e)MEU(e,e')=\sum_fP(F=f)MEU(F=f)=P(F=good)MEU(F=good)+P(F=bad)MEU(F=bad)=77.78$

날씨 예측이 좋고 나쁜 두 가지 경우이므로, 이 에비던스 값을 가중치로 준 MEU의 합이 날씨 F가 관측되었을 때 구할 수 있는 MEU다.

VPI는 이렇게 새로 얻은 에비던스로 만든 MEU에 구하기 전 MEU를 뺀 값이다.

$VPI(F)=MEU(F)-MEU(\empty)=77.78-70=7.78$

2. Properties of VPI

VPI는 다음과 같은 수학적 특성을 가진다.

• Nonnegativity: VPI는 언제나 양수다. 현재 가지고 있는 에비던스 집합에 없는 새로운 에비던스를 통해 더 정보가 주어진 informed 탐색이 가능하기 때문이다. expectimax 알고리즘의 계산 가용 깊이가 더 깊어진 것이라 이해하자.

• Nonadditivity: 새로운 에비던스 $E_J$와 $E_K$를 따로 관측한 VPI 두 개를 합한 값이 모두 관측한 VPI 값과 다를 수 있다.
  $VPI(E_j,E_k|e)\neq VPI(E_j|e)+VPI(E_k|e)$

• Order-independence: 에비던스 관측 순서가 달라지더라도, 얻는 VPI는 같다. 새로운 에비던스를 관측할 때까지 에이전트가 아무 행동도 하지 않기 때문에, 그때까지 연속된 특정한 절차적 여파가 노드 상에 미치지 않는다.
  $VPI(E_j,E_k|e)\neq VPI(E_j|e)+VPI(E_k|e,E_j)=VPI(E_k)+VPI(E_j|e,E_k)$