• 다음 내용은 [CS-188] Introduction to Aritificial Intelligence, UC Berkeley, Fall 2018의 Readings-Note8을 정리하였음을 밝힙니다.
• 스스로 이해하기에 영문 용어가 이해하기 직관적이면 그대로 사용했습니다.

Markov Models

랜덤 변수 사이의 밀접한 관계가 그래프 도식으로 표현된 베이즈 넷을 무한한 길이로 나타냈다고 가정해보자. 일련의 노드가 이어진 일종의 사슬과 같은 형태로 나타낼 수 있을 것이다.

마르코프 모델은 특히 그런 상태의 노드 하나가 현재 상태의 랜덤 변수 값을 담고 있으며, 연속된 노드를 통해 어떻게 값이 달라지는지 알려준다. 중요한 관건은 초깃값 노드와 트랜지션 함수만 주어진다면 특정 타임 스탬프 노드값이 어떤지 알 수 있다는 점이다.

• 초깃값 분포(initial distribution): 타임 스탬프가 0일 때 랜덤 변수의 값

• 트랜지션 모델(transition model): 타임 스탬프가 1씩 증가할 때 상태가 변환될 확률

$Pr(W_0)$을 초깃값 분포라고 할 때, 타임 스탬프 1에 올 랜덤 변수의 값은 자연스럽게 $Pr(W_{i+1}|W_i)$가 된다. 조건부 확률을 통해 다음 타임 스탬프 값을 구할 수 있다는 뜻은 물론 t=i+1이 t=i에 의존적임을 뜻한다.

어떻게 생각해보면 당연하다. 트랜지션 모델을 통해 확률 분포를 얻어내는 조건부 확률 수식에서 베이스가 되는 식이 한 차례 전의 상태이기 때문이다.

그런데 이보다 중요한 포인트는 t=i+1 상태의 랜덤 노드 값은 t=i를 제외한 다른 모든 노드와는 관계가 없다는 것이다.

• 마르코브 특성(Markov Property) / 메모리리스 특성 (memoryless property): t=i+1의 값을 구하기 위해서는 t=i 값과 (트랜지션 모델만) 있으면 된다.

마르코브 특성을 가정한다면 결합 확률 분포를 간략화할 수 있다.

$Pr(W_0,W_1,...,W_n)=Pr(W_0)Pr(W_1|W_0)Pr(W_2|W_1)...Pr(W_n|W_{n=1})=Pr(W_0)\prod\limits_{i=0}^{n-1}Pr(W_{i+1}|W_i)$

마르코프 모델의 또다른 중요한 특성은 트랜지션 모델이 시간과 관계 없이 일정한, 일종의 정지된 프로세스라는 것이다. $Pr(W_{i+1}|W_i)$은 모든 타임 스탬프 $i$에 있어서 동일하다.

정리하자면, 마르코브 모델의 타임 스탬프 t=i에 존재하는 랜덤 변수 값을 구하려면 초깃값과 트랜지션 모델 두 개만 주어지면 된다.

1. The Mini-Forward Algorithm

마르코프 모델의 특성을 통해 타임 스탬프 t에서의 결합 분포를 모두 계산할 수도 있지만, 연산 비용이 크다. 다른 모든 변수에 대해서 합계를 구하는 marginalize 과정이 필요하기 때문이다. 변수 j가 각각 d개의 값을 취할 수 있을 때 시간 복잡도 $O(d^j)$가 요구된다.

보다 효율적으로 t=i+1 타임 스탬프의 결합 분포를 구하는 방법을 알아보자.

1. t=i+1 타임 스탬프의 분포를 얻으려면 $Pr(W_i)$를 통해 타임 스탬프 t=i 단계의 확률 분포를 확인해야 한다.
2. t=0 초깃값 확률 분포부터 반복적으로 트랜지션 모델을 적용해 다음 단계 t=i+1의 확률 분포 값을 계산하자.

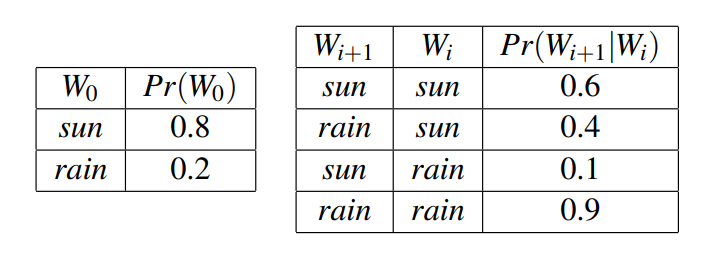
초깃값과 트랜지션 모델을 적용해 $Pr(W_1)$을 구해보자.

$Pr(W_1=sun)=\sum\limits_{w_0}Pr(W_1=sun|w_0)Pr(w_0)=0.6*0.8+0.1*0.2=0.5$
$Pr(W_1=rain)=\sum\limits_{w_0}Pr(W_1=rain|w_0)Pr(w_0)=0.4*0.8+0.9*0.2=0.5$

• $Pr(W_{i+1})=\sum\limits_{w_i}Pr(w_i,W_{i+1})=\sum\limits_{w_i}Pr(W_{i+1}|w_i)Pr(w_i)$

이 효율적인 테크닉을 통해 t=i에서의 확률 분포를 빠르게 계산할 수 있다. 그런데 이때 트랜지션 모델만 보고서도 다음에 어떤 값이 올지 알 수도 있다.

위 날씨 계산 모델에서는 t=0에서 t=1으로 타임 스탬프가 1 증가했을 때 비가 올 확률이 훨씬 늘어났음을 알 수 있다. 어떤 모델에서는 계속해서 타임 스탬프가 증가하더라도 랜덤 노드의 값이 바뀌지 않는 구간이 있을 것이다.

2. Stationary Distribution

어떤 타임 스탬프에서 랜덤 노드 값이 변화하지 않고 수렴할까? 정상 분포(stationary distribution) 계산을 통해 이 문제를 풀 수 있다. 정상 분포는 곧 $Pr(W_{t+1})=Pr(W_t)$인 타임 스탬프 t인 지점이다.

다시 미니-포워드 알고리즘에서 타임 스탬프 t 구간의 확률 분포 값을 구한 것을 가져와보자. 정상 분포 지점에서는 모두 같은 값이기 떄문에 = 관계로 표현할 수 있다.

• $Pr(W_{t+1})=Pr(W_t)=\sum\limits_{w_t}Pr(W_{t+1}|w_t)Pr(w_t)$

이 식을 통해 날씨가 맑거나 비가 올 확률이 수렴하는 구간을 구해보자.

$Pr(W_t=sun)=Pr(W_{t+1}=sun|W_t=sun)Pr(W_t=sun)+Pr(W_{t+1}=sun|W_t=rain)Pr(W_t=rain)=0.6*Pr(W_t=sun)+0.1*Pr(W_t=rain)$
$Pr(W_t=rain)=Pr(W_{t+1}=rain|W_t=sun)Pr(W_t=sun)+Pr(W_{t+1}=rain|W_t=rain)Pr(W_t=rain)=0.4*Pr(W_t=sun)+0.9*Pr(W_t=rain)$

특정 타임 스탬프 t에서의 각 상태별 확률을 모두 더하면 1이라는 점을 기억하자. 정상 분포의 성질을 사용해 구한 위 식과 함께 이차 방정식처럼 풀면 각 확률 값을 구할 수 있다.

$Pr(W_t=sun)=0.2, Pr(W_t=rain)=0.8$

정상 확률 분포라는 마르코브 모델의 특성을 통해 강력한 일반화가 가능하다.

• $Pr(W_t)=\sum\limits_{w_t}Pr(W_{t+1}|w_t)Pr(w_t)$

$W_t$를 이루는 도메인의 크기 $k$번만 방정식을 풀면 위 식을 얻을 수 있다.