이산수학 부울대수와 논리회로설계

Ja_an·2021년 7월 15일

이산수학

목록 보기

4/13

논리회로설계 문제를 푸는 과정

논리회로설계 문제 → 입력,출력 정의 → 부울함수 정의 → 부울식 생성 → 부울식 최소화 → 논리회로

⇒ 논리회로설계 문제를 풀기위해 부울대수 필요

어떤 명제의 참과 거짓을 이진수 1과 0에 대응시켜서 명제와 명제간의 관계를 수학적으로 표현하는 것이다
종류
- 보수
  - '로 표시
  - 0' = 1, 1'=0
- 부울 합
  - - (또는 or)로 표시
    1+1=1
    1+0=1
    0+1=1
    0+0=0
- 부울 곱
  - · (또는 and)로 표시 (·는 생략하여 표기하기도 함)
    
    1 · 1=1
    1 · 0=0
    0 · 1=0
    0 · 0=0
- 연산 우선순위 : 보수 > 곱 > 합
부울 변수
- 집합 S={0,1}의 원소 값만 갖는 변수
부울 함수
- 0 또는 1의 입력값들에 대하여 0또는 1의 출력값을 갖는 함수
부울 식
- 하나 또는 여러개의 변수나 기본 연산들이 결합하여 만들어진 형태
- 0, x, y 와 같은 하나의 부울변수 또한 부울 식으로 볼 수 있다
항등(equivalent)
- n개의 변수로 이루어진 부울 함수 F, G가 있을때 모든변수 x1, x2, ..., xn 값에 대하여
  F(x1, x2, ..., xn) = G(x1, x2, ..., xn)
  이면, 부울함수 F와 G는 동등(equivalent)하다고 한다
- 동일한 변수값에 대해서 진리표의 결과값이 동일하면 두 부울 함수는 동등하다
부울 대수의 법칙

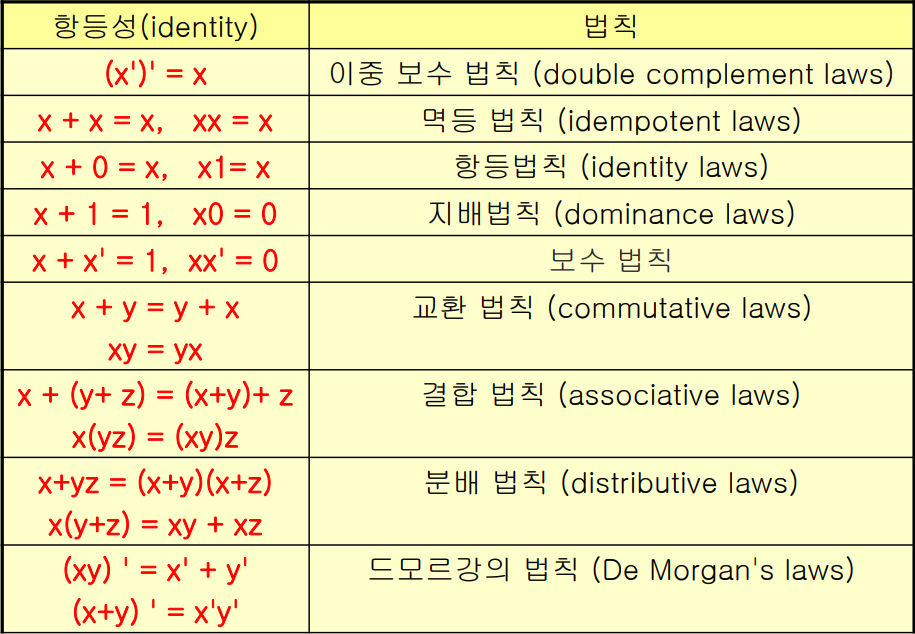
증명방법
1. 연산의 정의에 따라 진리값을 만들어 보여주는 방법
2. 이미 증명된 명제(규칙)를 이용해 증명
  
  x(x+1) = x 증명
  x(x+1)
  = (x+0)(x+y) (항등법칙)
  = x+0y (분배법칙)
  = x+y0 (교환법칙)
  = x+0 (지배법칙)
  = x (항등법칙)
정리: 쌍대성의 원리 (duality principle)
- 주어진 부울식과 그것의 쌍대는 진리값이 같다
- 부울 대수의 쌍대는 · 과 +를 교환하고, 0과 1을 교환하여 구할수 있다
- 부울 대수의 모든 항등 법칙에 대하여 다음 2개의 식이 쌍으로 존재한다
  x+0 = x , x · 1 = x
  이러한 쌍을 쌍대(dual)라고 한다
최소항
- 함수의 모든 변수에 대하여 부울 곱의 형태로 표현한 것으로
  각 변수는 원래 형태 또는 보수형태로 1개만 나타난다
논리합 형식 : 곱들의 합
- 부울 함수를 최소항들의 부울 합으로 나타내는 형식
- 함수의 값이 1이되는 변수값의 조합들에 대하여 최소항들을 구하고,
  그 최소항들의 부울합을 취하면 부울 식을 구할 수 있다
부울 함수 → 부울 식 예시

x y F(x,y)
1 1 1 ⇒ xy
1 0 0
0 1 1 ⇒ x'y
0 0 1 ⇒ x'y'
⇒ F(x,y) = xy + x'y + x'y'