지난 시간까지 배운 것
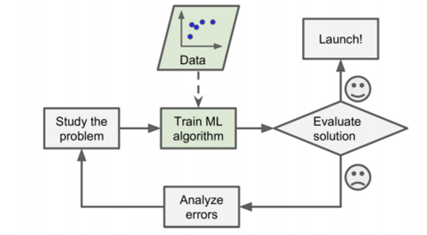
▶ 지도학습 (라벨을 달아주는 것 = 정답을 알려주는것)
- 데이터를 기반으로 하는 문제 해결 방법
- 문제 분석 > 학습 시킴(데이터 계속 유입됨) > 데이터를 베이스로 하기 때문에, 알고리즘 구현 & 서비스 런칭 부분만 코딩으로 해결
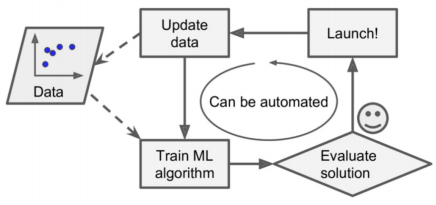
- 모델 스스로
데이터 수집 > 트레이닝 > 업데이트(평가, 런칭) > 데이터 유입
- 회귀 모델
- 1차 함수
- 기울기 & y절편이 있음
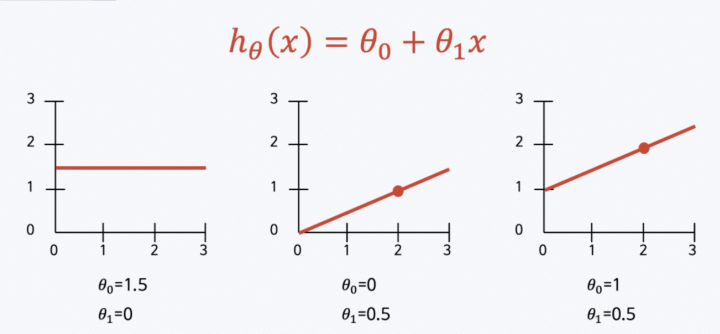
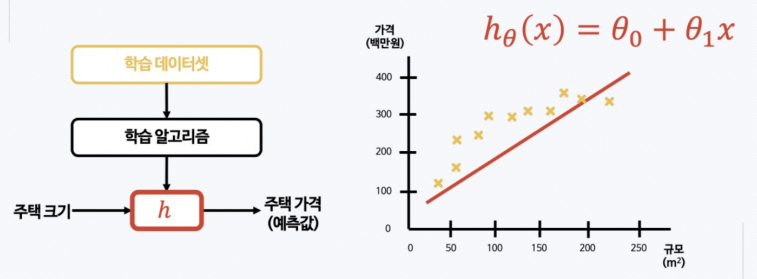
- 선형 회귀
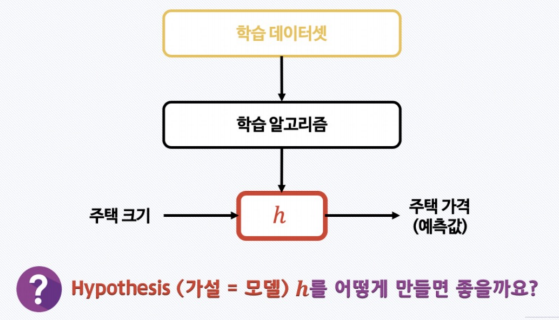
- 내가 가지고 있는 데이터와 가장 잘 맞는 직선을 찾겠다
- 그리고 그 직선을 hypothesis 라고 한다
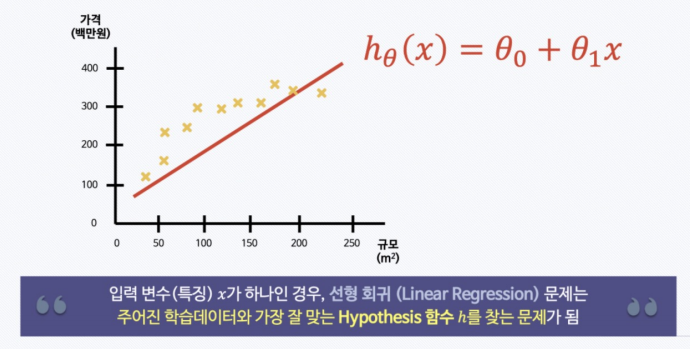
1. OLS : Ordinary Linear Least Square
1_기본 예제
# !pip install statsmodels# 1) 데이터 설정
import pandas as pd
data = {'x':[1.,2.,3.,4.,5.], 'y':[1.,3.,4.,6.,5.]}
df = pd.DataFrame(data)
df# 2) 가설 세우기
import statsmodels.formula.api as smf
# formula="y~x" : y=ax+b 라는 의미를 내포
lm_model = smf.ols(formula="y~x", data=df).fit()# 3) 결과
lm_model.params# 4) seaborn
import matplotlib.pyplot as plt
import seaborn as sns
plt.figure(figsize=(10,7))
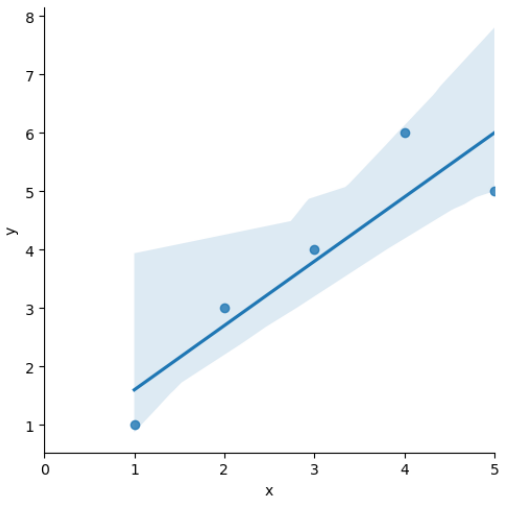
sns.lmplot(x='x', y='y', data=df);
# xlim : plt 축 범위 설정 함수, x축 범위 지정
plt.xlim([0,5])2_잔차 (resid) 평가
- 잔차 란?
- 내 모델과 실제 값의 차이
- 잔차 평가는 잔차의 평균이 0(=이라서 회귀하는 것임)이고 정규분포를 따라야 함
# 잔차 확인
resid = lm_model.resid
resid▼ 에러값s
0 -0.6
1 0.3
2 0.2
3 1.1
4 -1.0
dtype: float64
3_R-Squared (결정계수)
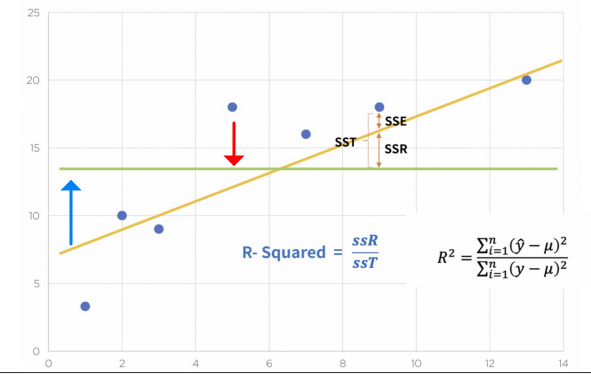
- 녹색 : 평균
- 분모 : 참값(점)이 가지는 평균으로 부터의 오차(점~녹색 거리)
- 분자 : 예측값(노랑~녹색 거리)으로 부터 가지는 평균으로의 오차
- 참값 = 예측값 : 1
참값이 예측값과 일치한다면 1임
- (기본) 결정계수 구하기
import numpy as np
# df의 y컬럼 평균을 mu로 잡음
mu = np.mean(df['y'])
y = df['y']
# 예측값(y_hat)
y_hat = lm_model.predict()
# 합계
# 분자(예측값-평균)^2 / 분모(참값-평균)^2
np.sum((y_hat - mu)**2 / np.sum((y - mu)**2))0.8175675675675673
- (쉽게) 결정계수 구하기
lm_model.rsquared0.8175675675675677
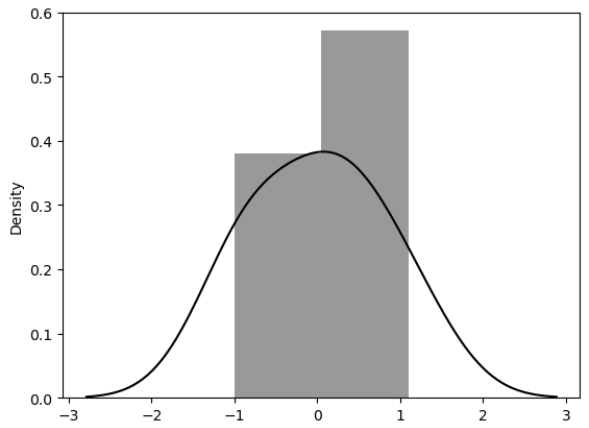
- 분포도 확인
# 잔차의 분포도 확인
sns.distplot(resid, color='black');2. 통계적 회귀
# 모듈
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns# 1) 데이터 로드
data_url = 'https://raw.githubusercontent.com/PinkWink/ML_tutorial/master/dataset/ecommerce.csv'
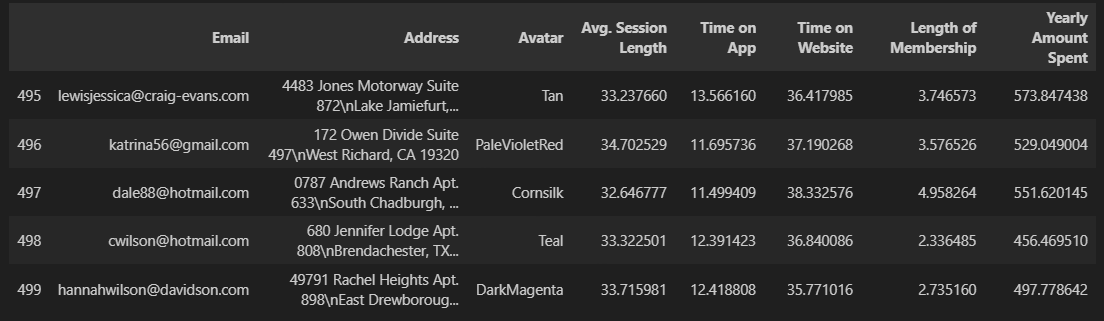
data = pd.read_csv(data_url)# 2) 구조 확인
data.tail()# 3) 컬럼 확인
data.columnsIndex(['Email', 'Address', 'Avatar', 'Avg. Session Length', 'Time on App',
'Time on Website', 'Length of Membership', 'Yearly Amount Spent'],
dtype='object')
# 4) 필요 없는 컬럼 삭제
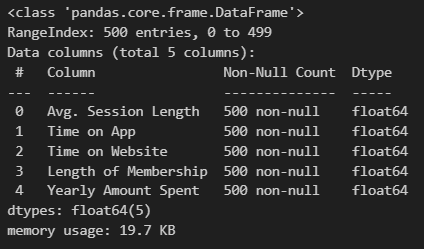
data.drop(['Email', 'Address', 'Avatar'], axis=1, inplace=True)
data.info()# 5) 컬럼별 boxplot
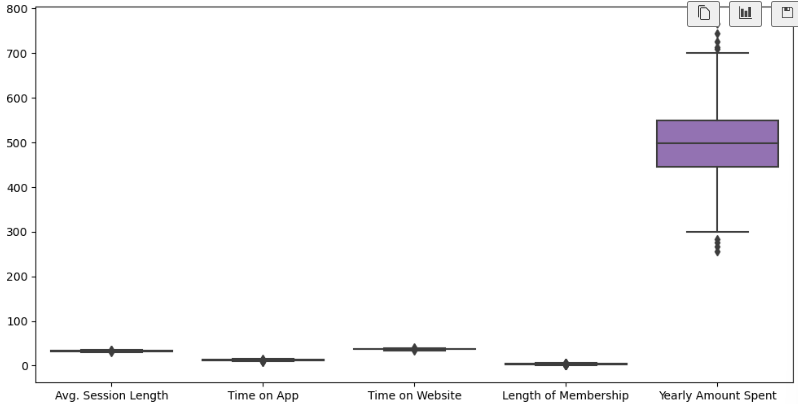
plt.figure(figsize=(12,6))
sns.boxplot(data=data);# 6) 특정 칼럼 다시 boxplot
plt.figure(figsize=(12,6))
sns.boxplot(data=data.iloc[:, :-1]);-
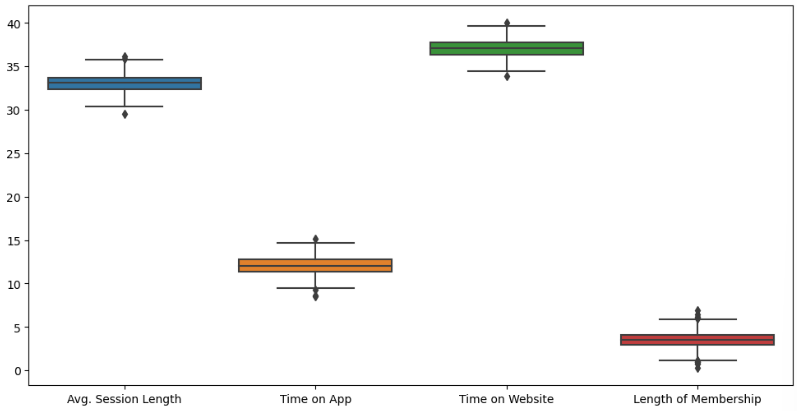
-
data.iloc[:] -
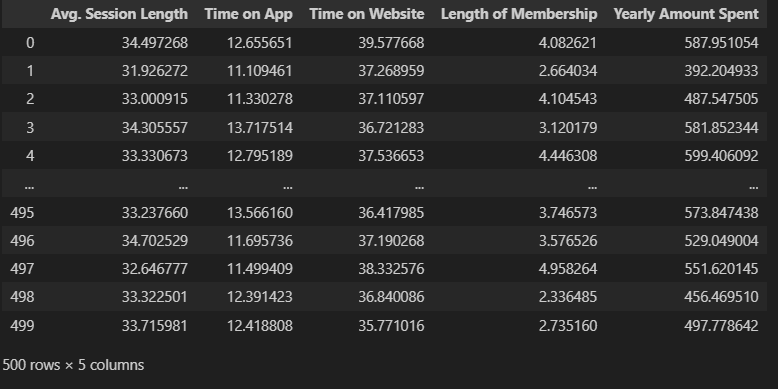
-
data.iloc[:, :-1] -
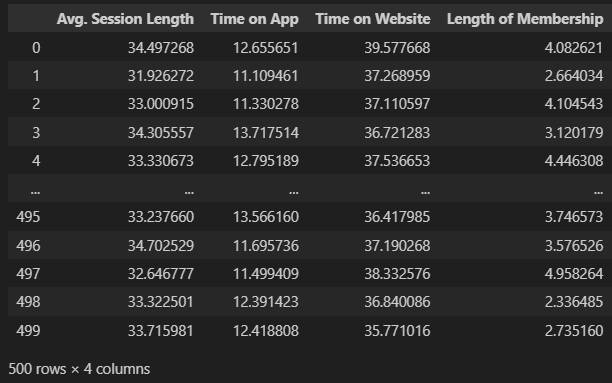
-
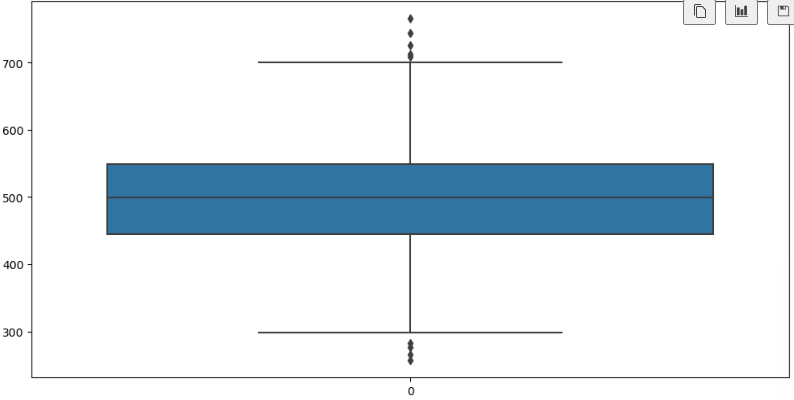
# 7) label 값에 대한 boxplot
plt.figure(figsize=(12,6))
sns.boxplot(data=data['Yearly Amount Spent']);# 8) pairplot으로 경향 확인
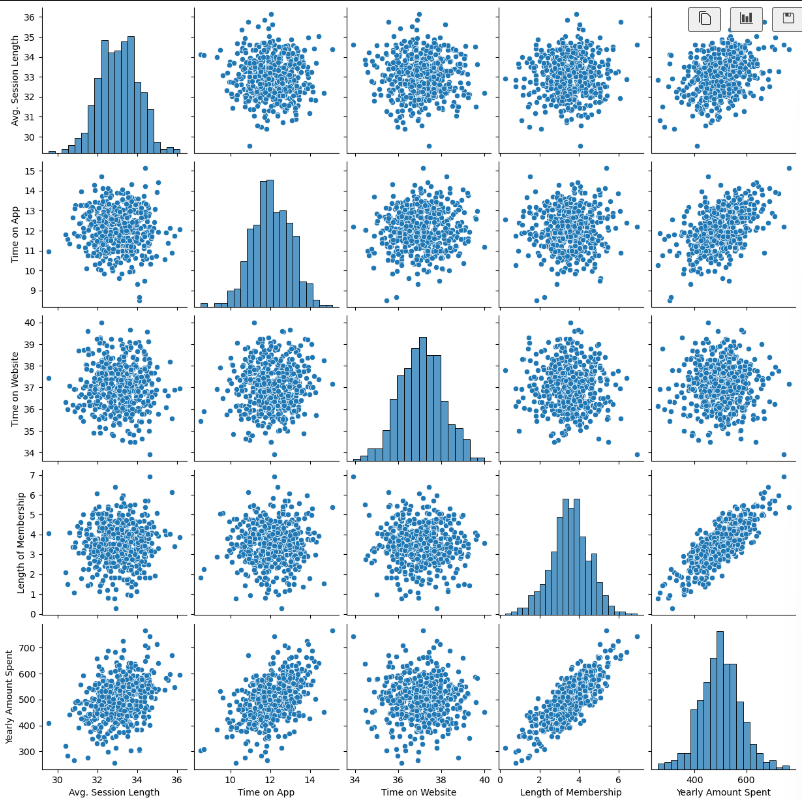
plt.figure(figsize=(12,6))
sns.pairplot(data=data);# 10) 상관관계를 갖는 것을 lmplot으로 확인
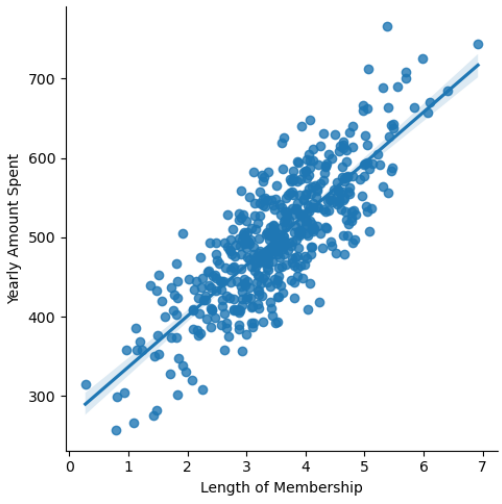
plt.figure(figsize=(12,6))
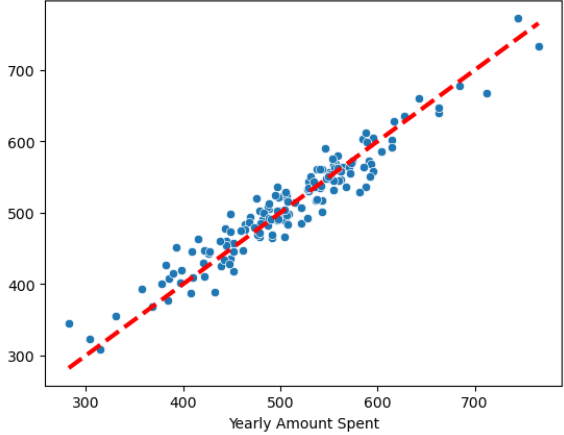
sns.lmplot(x='Length of Membership', y='Yearly Amount Spent', data=data);# 11) 상관이 높은 멤버십 유지기간 만 가지고 통계적 회귀
import statsmodels.api as sm
X = data['Length of Membership']
y = data['Yearly Amount Spent']
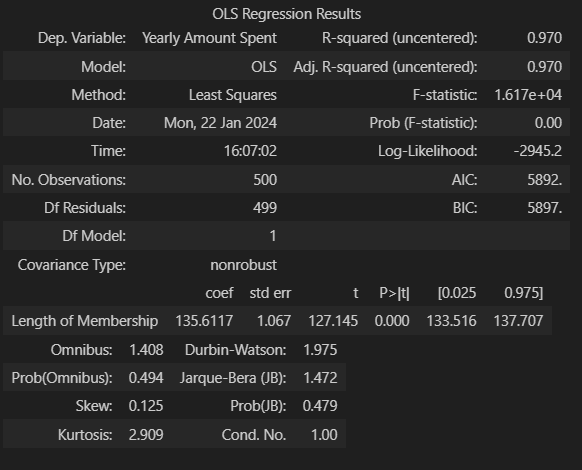
lm = sm.OLS(y, X).fit()
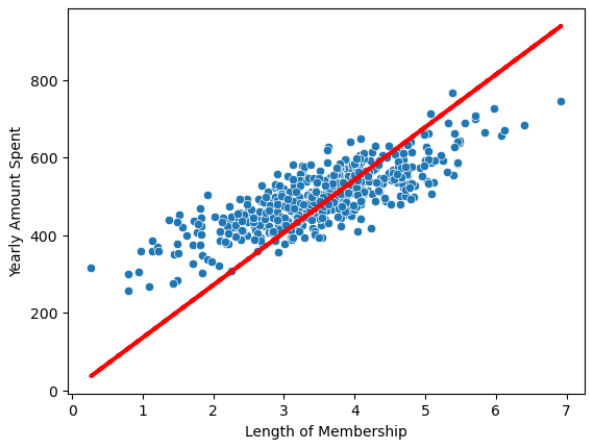
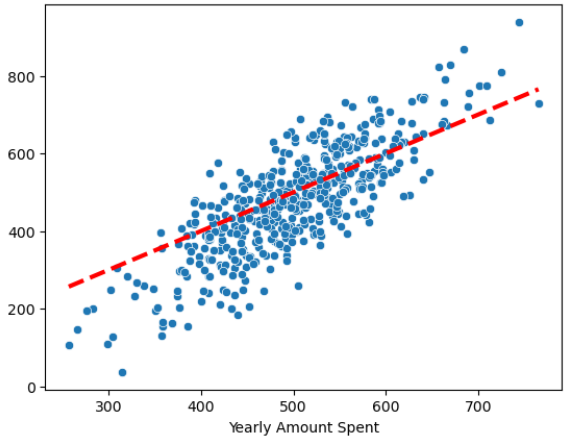
lm.summary()# 12) 회귀 모델 그리기
pred = lm.predict(X)
sns.scatterplot(x=X, y=y)
plt.plot(X, pred, 'r', ls='dashed', lw=3)# 13) 참 값, 예측값 그리기
sns.scatterplot(x=y, y=pred)
plt.plot([min(y), max(y)], [min(y), max(y)], 'r', ls='dashed', lw=3);# 14) 참 값, 예측값 그리기
sns.scatterplot(x=y, y=pred)
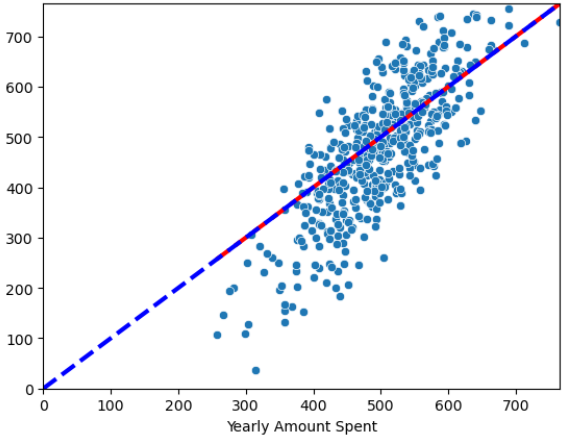
plt.plot([min(y), max(y)], [min(y), max(y)], 'r', ls='dashed', lw=3);3
plt.plot([0,max(y)], [0, max(y)], 'b', ls='dashed', lw=3);
plt.axis([0,max(y), 0, max(y)])# 15) 상수항 추가 (열추가)
# c_를 해주면 바아로 삽입됨
# 추가 [원래 X에, 1을 X의 길이 만큼 만들어서]
X = np.c_[X, [1]*len(X)]
# 잘 추가 됐는지 5개만 보기
X[:5]array([[4.08262063, 1. ],
[2.66403418, 1. ],
[4.1045432 , 1. ],
[3.12017878, 1. ],
[4.44630832, 1. ]])
# 16) 다시 fit()
lm = sm.OLS(y, X).fit()
lm.summary()-
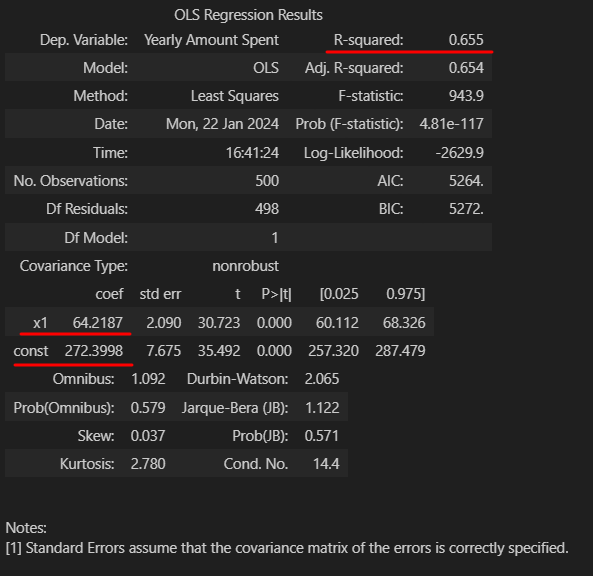
- 아까와는 다르게 x1의 밸류와 constant가 잡힘
- R aquared가 작아짐
- R aquared : 평균을 기준으로 데이터가 얼마나 예측과 실체값 간의 편차
- AIC 가 작아짐 (낮을 수 록 좋음)
- AIC : 내가 만들어낸 모델이 나의 데이터를 얼마나 잘 반영하는지 측정하는 도구 (=원래 정보를 얼마나 손실 시키는지의 정도)
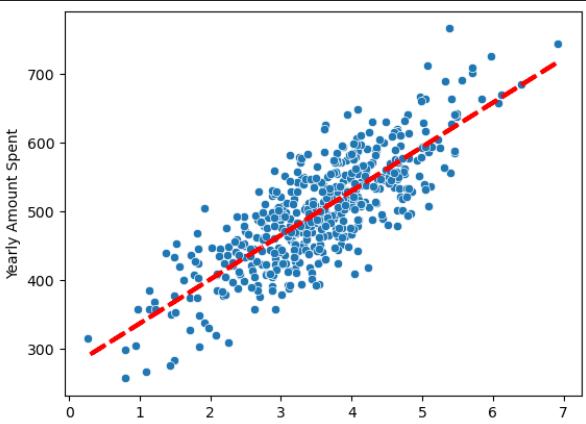
# 17) 다시 선형 회귀
pred = lm.predict(X)
sns.scatterplot(x=X[:, 0], y=y)
plt.plot(X[:, 0], pred, 'r', ls='dashed', lw=3)# 18) 참 값, 예측값 그리기
# (x=참값, y=예측값)
sns.scatterplot(x=y, y=pred)
plt.plot([min(y), max(y)], [min(y), max(y)], 'r', ls='dashed', lw=3);# 19) 데이터 분리 후
from sklearn.model_selection import train_test_split
X = data.drop('Yearly Amount Spent', axis=1)
y = data['Yearly Amount Spent']
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=13
)# 20) 4개 컬럼 모두 변수로 회귀
import statsmodels.api as sm
lm = sm.OLS(y_train, X_train).fit()
lm.summary()-
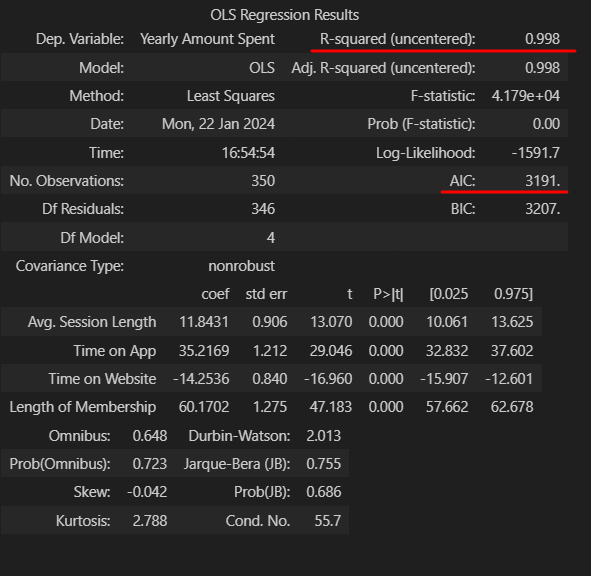
-
이전 값보다
- R aquared가 높아짐
- AIC 가 작아짐 (낮을 수 록 좋음)
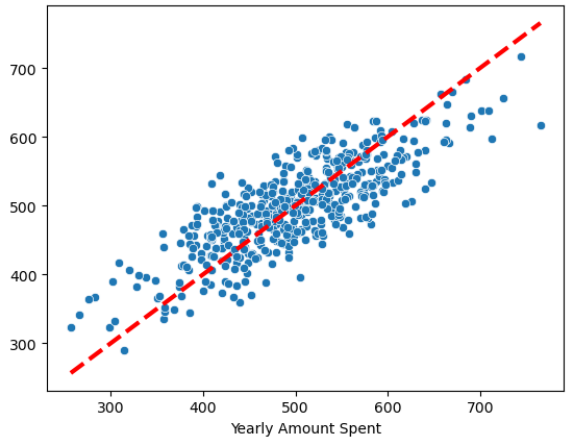
# 21) 참값 vs 예측값
pred = lm.predict(X_test)
sns.scatterplot(x=y_test, y=pred)
plt.plot([min(y_test), max(y_test)], [min(y_test), max(y_test)], 'r', ls='dashed', lw=3);